はじめに

この記事の概要

1. 斜線であるかどうかは、我々の視点(パース)によって変わる
2. 本来直線(水平線・垂直線)であるのに、斜線に見えるということはパースがかかっている
3. パースがかかっているということは線が消失点へ向かって伸び、集束している
4. 線が集束するかしないか(直線にみえるか斜線にみえるか)は、透視図法(一点、二点、三点等)次第である

この記事の動画説明

 

この記事の目的

建築学的な専門的なパース知識ではなく、「線画」に対する理解を深めることに目的をおきます。家は建てられずとも、よりリアルな家や街等が描ければそれでもいいのです。また専門的に描きすぎると絵の個性や良さが無くなるといった影響もあります。芸術にとって「リアリズム(写実性)」は美の価値観のひとつにすぎません。二次元的な絵はある意味で「抽象派」であり、ある意味では「写実派」です。両方学んでそのバランスを自分でとっていきましょう。

建築学的な知識も創造の素材となる要素なので、できるだけ少しでも学びたいと思っています。専門的な知識が必要な人にも、少なくともその導入や興味のきっかけとなるように努めます。

定義

斜線的であること

・斜線(しゃせん,Diagonal line):私が使う「斜線的であること」の定義は、自分の視点において、水平線的あるいは垂線的ではない線であり、斜めになっている直線のことです。「斜線」の一般的な意味は一つの直線または平面に、ななめに交わる直線のことです(角度は問いません)。

同じ立方体の面であるのに、見方によって線が直線に見えたり、斜線に見えたりします。この理由をこの記事では説明しています。さらに直線を水平的と垂直線にわけて説明します。結論から先取りすれば、パースがかかっているからであり、線が消失点へと伸びている(集束していく)からです。

水平的であること

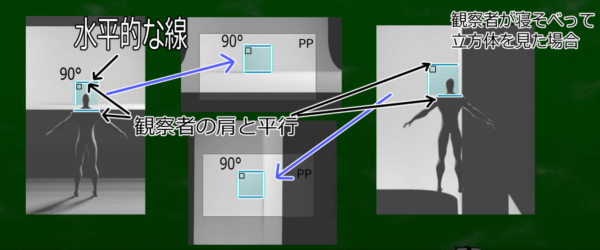
・水平線(すいへいせん,Horizontal line):私が使う「水平的な線」とは、観察者の肩と平行な横にまっすぐと伸びる線を意味しています。地平線の彼方、水平的の彼方といった使い方ではありません。

人間(観察者)が立方体を見る場合で、四角く囲まれた範囲を「画面(PP)」とします。人間ではなくても、カメラでもかまいません。カメラを覗き込んだときの四角い画面でもかまいません。

人間の肩は比較的、直角線に近いですよね。この性質を利用して、人間の肩と同じような角度(９０°)に伸びる線を水平線と定義したのです。

観察者が寝そべって立方体を見ると、肩の位置が変わります。したがって、水平線の位置も変わります。水平線かどうかは観察者の視点次第で変わるということです。さきほど水平線であった線は、縦に真っ直ぐ伸びる線になります。これを垂直線といいます。水平線と垂直線は同じ線を視点によって言い方を変えているだけです。

垂直的であること

・垂直線(すいちょくせん,vertical line):私が使う「垂直的な線」は、観察者の肩と直角に交わる縦にまっすぐ伸びる線を意味しています。

これは二点透視図法における立方体です。さきほどの一点透視図法における立方体のような「水平的な線」はありません。垂直線な線かどうかの判断基準は、観察者の肩です。観察者の肩に直角に交わるような、縦の線があれば垂直線として扱います。立方体の他の線は斜線的に見えますよね。斜線的であるということは、観察者の肩と平行ではないということであり、また垂直的でもないということでもあります。ざっくりと扱えばそういうことになります。

斜線的である線の例

具体例：立方体の線は斜線的か？

たとえば一点透視図法的な視点で、立方体を正面からの視点で見てみます。線は水平線(水平な線という意味です)、あるいは垂線です。垂線か水平線かというのは物体に依存しているものではなく、視点によります。例えばこの立方体を寝っ転がって見たら、水平的な線と垂線的な線は逆になります。

それではこれはどうでしょうか。垂線と垂線的が両方存在しています。先程の線を回り込んで見ただけです。

立方体自体はなにも変化していませんが、立方体を見る視点が変わるだけで水平的だった線が、斜線的に見えます。

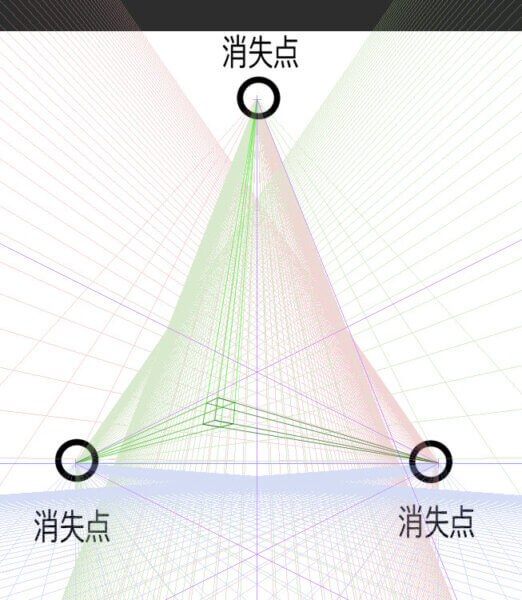
立方体のすべてが斜線的に見える視点のひとつの例が三点透視図法です。

斜線的かどうかは、視点に依存している

物自体の形と、我々に見える形は違う

たとえばこの一点透視図法の立方体を見てください。このケースでは立方体が電車のように一列につながっているような、長方形型になっています。

透視図法でいうところの「消失点」へ向かっています。その消失点が1点しかないので、一点透視図法というのです。

また、消失点へ向かう線が斜線的になるというのもポイントです。

この長方形を真横から見ると、斜線的には見えません。水平線的に見えます。

ちなみにこの長方形をどこまで伸ばしていっても、消失点へと物理的に届くことはありません(今回のケースでは観察者も立方体に沿って移動しています)。地球は丸いので、一周して自分のもとに帰ってくるかもしれません。仮に宇宙に向かって真上に伸ばしたとしても、消失点へ届くことはありません。消失点は別名、虚構点ともいいます。物理的に存在する点ではないのです。無限に続きます。

三次元ソフトでは消失点付近へ届くとオブジェクトが消えて見えなくなります。オブジェクトも消失するのでわかりやすいですね。二次元ソフト、たとえばクリップスタジオペイントでは”自分で”消失点の位置を決めます。二次元ソフトでは物理的に消失点があります。

斜線的であるかどうかは、こちらの見方に依存しているといいました。たとえばまっすぐ水平に伸びている定規を斜めにしてみてください。斜線的になりました。自分の視点が変わっていなくても、物体のほうが変化しても斜線的に見えるようになります。

これはさきほどの立方体を回転させたケースです。視点はほとんど変化していません。この面は消失点へ集束しません。斜線上に永遠に伸びるだけです。一点透視図法では、もし回転させなくても、最前面は真上や真横に永遠に伸びるだけで集束しないのです。二点透視図法ではさらに集束する線が１つ増え、三点透視図法では全ての立方体の線が集束するようになります。

視点が同じで、立方体が回転しただけでは、何ら消失点に変化がないのか？という問いは面白いと思います。そのためにはそもそも一点透視図法とはなにか？から説明する必要があります。機会があれば次に検討したいと思います。

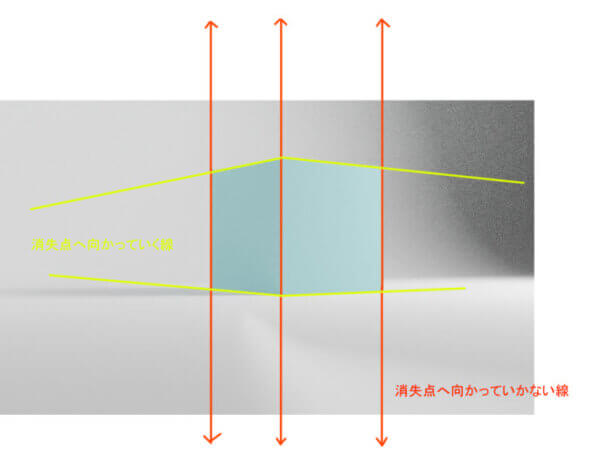
集束しない線について

比率について

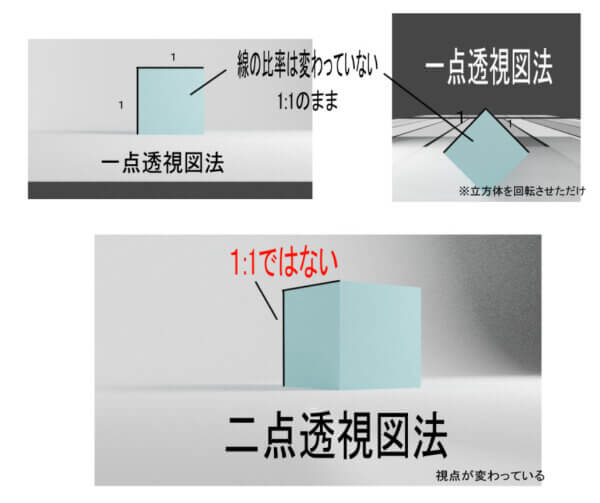
ざっくり整理するとこうなります。パースがかかるということは、”我々の見え方”において線が歪んで見えるということです。そして一点透視図法では、特定の面が一切歪んでいないというのがポイントです。上の画像で言えば、比率が一切替わっていません。つまり、”我々の見え方”と”実際の対象物”の形が一致しているということです。パースがかかっているということは、それらが一致していないということです。このことを次にもうすこし確認します。

ただし先程触れたように、立方体の回転のさせかた次第では、比率が変わります。このことは今回扱いません。次回触れたいと思います。

消失点を持たないように見える視点(一点透視図法)

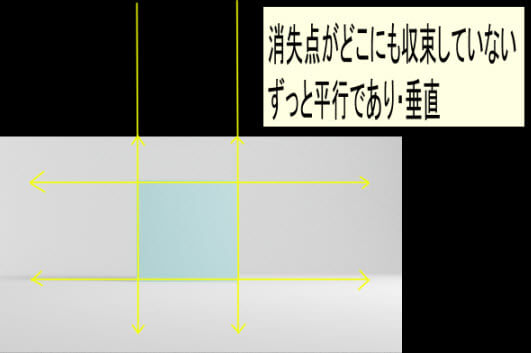
この立方体の面を見てください。縦と、横に線が伸びていると仮定しても、永遠に平行のままで収束しません。つまり、消失しないということであり、消失点をもたないということです。

専門的に言えば違うのかもしれませんが、ともかく私には集束している見えないのです。延々と平行であり、そして垂直に伸びていきます。これらの線はどこかで交わることもなく、おそらく交わろうとさえしないのだと思います。

一点透視図法ではこのような、集束しない線で形成される面が１つあるというのがポイントだと思います。

ではこのような視点はどうでしょうか。これも一点透視図法です。これも先程と同じように、集束しない線があることに気づいたと思います。”我々に見える”最も前にある面の線の比率は1:1のままですよね。一切歪んでいません。

この動画を見てみれば、さらに言っていることがよく分かると思います。これは”わざと”歪ませました。画角や焦点距離が関係しているのですが、今回はふれません。

しかし歪んでいる線があることがわかると思います。そうです、”我々に見える”最も前にある面以外の線です。しかもそれはすべて「斜線」です。

大事なのは、歪んでいるのは消失点へと”集束”している線だということです。集束していない線は歪んでいないのです。専門的な理解からして正しいかどうかはおいておいて、斜線が他と比較して歪んで見えているというのは抑えておくべきポイントだと思います。

消失点を持たないように見える視点(二点透視図法)

二点透視図法でも消失点を持たない線があります。それは垂直線です。

二点透視図法では、垂線は歪まないのですが、他の線は”すべて”斜線的になるので歪みます。歪むということが、パースがかかるということです。実際に立方体が斜線的な構造をしているわけではないのにもかからず、斜線的に見えること、それがパースなのです。

斜線はいつも、消失点へ向かって伸びていきます。消失点は水平線のどこかに位置しています。一点透視図法なら視点の真ん中に、二点透視図法なら水平線の左右のどこかにあります。消失点は物理的にあるわけではありません。人間がジャンプすれば、消失点もついてきます。

細かく煩雑なパースの知識は置いておいて、物体それ自体と、我々に見えている物体は違うということの理解がとりわけ重要だと私は思います。カントの哲学みたいな話でわりと好きですこの考え。物自体は、大雑把に言えばものさしで測ったりして一片が何センチの云々カンヌンという情報にあたるのでしょうかね。

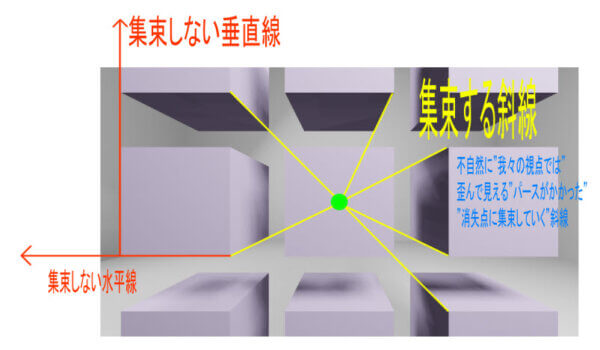
三点透視図法はお察しの通り、すべて斜線でできています。

クリスタにおけるそれぞれの消失点

これも今回は軽く触れるだけにします。二次元のイラストソフトでは物理的な点が用意されています。ただし、集束しない線はいくらのばしても物理的な点が用意されていません。三点透視図法では全ての線が集束しますが、一点や二点透視図法だと集束しない線があります。

【クリスタ】視円錐(パース)を使って立方体を描く方法【CLIP STUDIO PAINT】

クリスタでのパースの作成方法については、以前記事を作ったのでそちらを参照してください。

参考文献

初心者でもわかりやすい本

ロビー・リーさんのほうがどちらかといえば用語集もあり、言葉の定義の説明が多くわかりやすいです。デヴィッド・チェルシーさんは用語の定義や説明が少ないですが、その分絵が多く、わかりやすいです。私はデヴィッド・チェルシーさんの後でロビー・リーさんの本を読みました。デヴィッド・チェルシーさんが言っていたことは、そういうことだったのか！と、はじめて理論的に理解できた記憶があります。

個人的には両方もっておくと便利だと思います、内容は重なる部分が多いですが、理解のための視点や説明が違います。

中級者向けの本

こちらはパースの基礎知識を理解した上で、さてどうやって絵に取り入れていこうかといったような応用的な部分が多いです。特にスコット・ロバートソンさんの本はかなり難解です。ある意味、建築学的なパース知識に近いと思います。しかし実用的な知識が多いです。高いですが、もっておいてもいいのではないかと思います。