目次
はじめに
動画での説明
・この記事の「概要・要約」はyoutubeの動画の冒頭にありますのでぜひ参照してください。
よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m
はじめに
軽く前回の復習をしておこう。
二点透視図法とはなにか、意味、定義、わかりやすく解説
二点透視図法:左右の2つの消失点を使う線遠近法のこと。
二点透視図法では縦の線が収束せず、奥行き方向と横方向の線がそれぞれ異なる消失点に収束する。
二点透視図法の種類を整理するとこのような図になる。
視円錐の計算式
今までの動画の知識を総動員して、二点透視図を作っていこう。
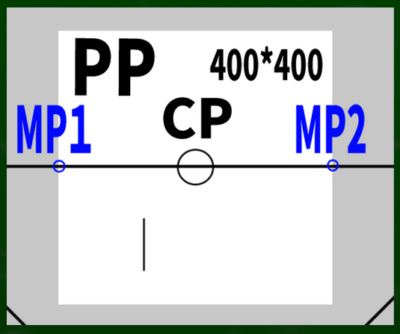
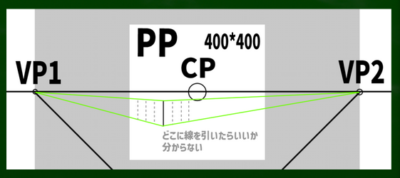
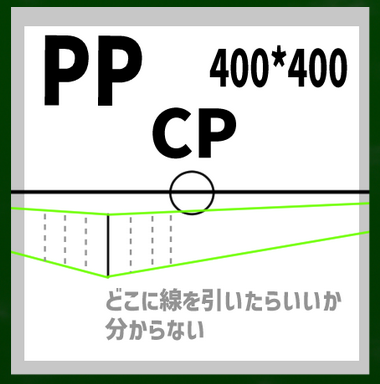
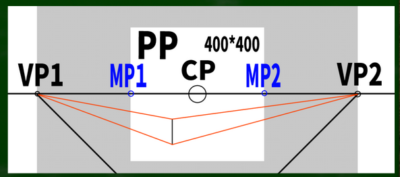
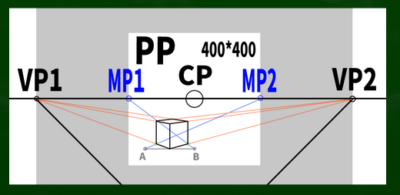
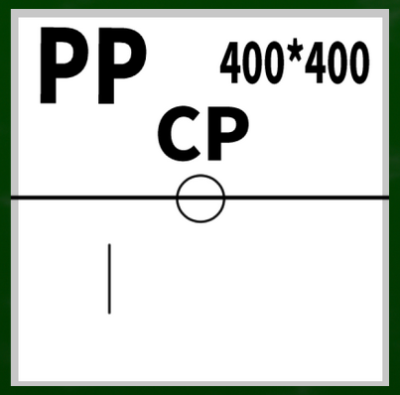
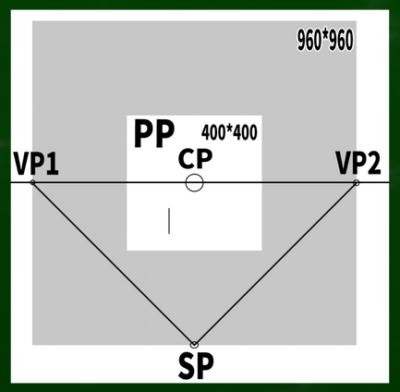
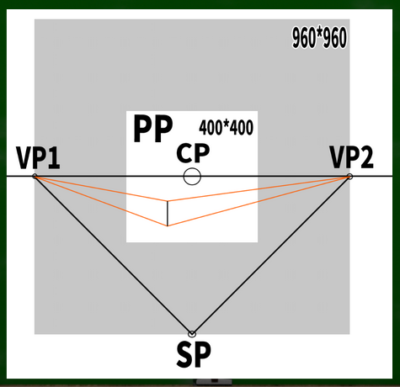
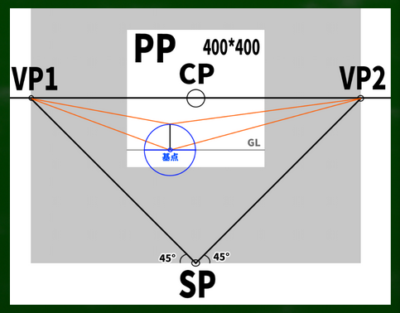
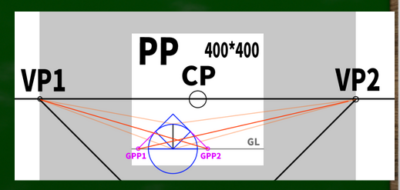
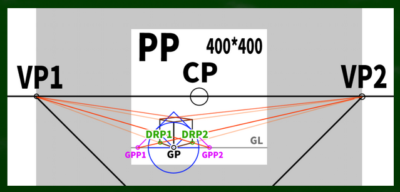
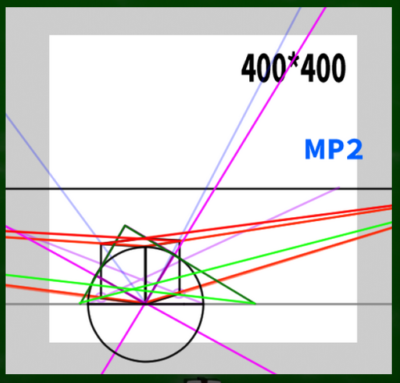
まずは基本の「二点平行透視図」の左右均等のケースを想定する。そして画面(キャンパス)は400*400(ピクセル)という単純なケースで作画していこうと思う。
以前考えた計算式を図にするとこのようになる。
【第四回】パースの基礎を学ぶ:パースにおける視円錐とはなにか、その設定方法
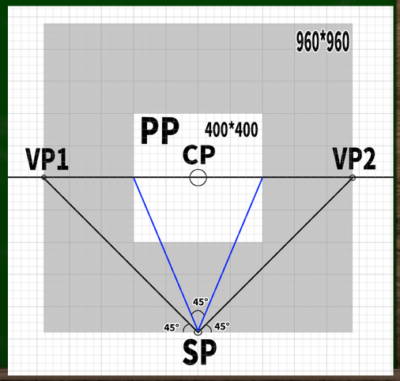
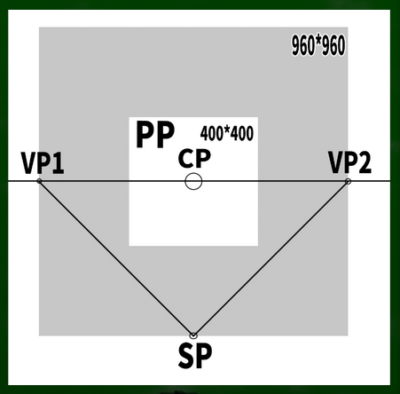
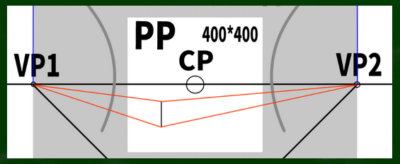
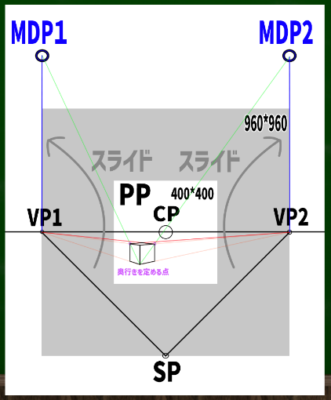
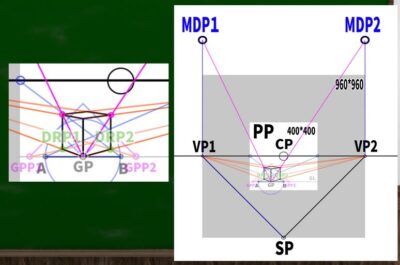
もし400*400の画面(PP)に45度視円錐でぴったりと収めようとするなら、消失点は960*960の円周上に近似的に収まることを第四回の動画で学んだ。
計算式は400*2.4=960である。※さらに視円錐で画面を覆い尽くしたい場合は、X(正方形の一辺)=√幅の二乗+高さの二乗を用いる。この場合、565となり、それに2.4を掛けた数値は1356となる。今回は960を用いる。
今回主に使う基本の透視図法の形
図にするとこのようになる。
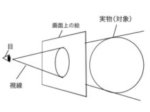
CPは視心、SPは立点、VPは消失点、PPは画面である。
直方体と立方体の違いとはなにか、意味、定義、わかりやすく解説
立方体(立方体):6つの面がすべて正方形である正六面体。辺の長さがすべて等しく、全ての角が直角(90°)である多面体
直方体:6つの面すべてが長方形で構成される三次元図形。対面する2つの面は互いに合同で平行、全ての角は直角(90°)である。
立方体は直方体の特殊ケースということになる。いろいろな四角い箱があるが、サイコロのように各辺が等しい箱を特に立方体と呼ぶわけである。
さて、ここから「適当な直方体」を描くなら簡単である。まず、描きたい直方体の垂線を描く。次にその垂線からVPへと線を伸ばしていく。
後は「適当な奥行き」を定めて、立方体を作成すればいい。
今は特に「立方体」を描こうとしていない。つまり、実測の全ての辺の数値が等しいサイコロのような立方体を描こうとしていない。勘で奥行きを決めただけである。もちろん描きたい正しい比率の直方体を描こうとすれば別の話になるが、今は適当に、直感的に描こうとしているだけである。
追記(2025/05/08):どうやら立方体と正六面体を混同して、「正立方体と表記してしまっていたようだ。そもそも立方体を直方体ないし単なる立体として認識してしまっていたのかもしれない。正方形で構成される立体が立方体であることを修正しておく。
もっとも、フリーハンドで「形がそれっぽく見える技術」こそが大事だという点は心に留めておいたほうがいいのかもしれない。
いずれにせよ正解を知らないとフリーハンドで違和感を獲得して修正していくスキルも得られないだろう。それゆえに一度正解の形を描いてみるという作業は得るものがあるはずである。たとえばデッサンで模写する絵そのものを使わないとしても、そのもの(要素)を超えた正しい、あるいは自然な、美しい比率(関係)というものが体得されるのと似ている。
「立方体の奥行きを決める指標の点」がわからない問題
立方体を描くとすれば、どのあたりに奥行きを設定すればいいのかという「指標」が必要になる。
しかし、今まで記事で学んだ知識ではその指標がない。それゆえに、指標を学ぶ必要がある。
二点透視図法で立方体を描く方法の種類
図での説明
図にするとこのようなイメージとなる。なお、以前の動画で一点透視図法で立方体を作ったときの手法はこの中だと「測点法」であり、その中でも「距離点法(D点法)」と呼ばれるものである。
まだ平面図の手法を詳しく扱っていないので、今回は平面図を用いないで済む測点法と介線法を中心に扱いたい。基線法は最後にすこしだけ扱う予定である。
なお、どの手法を用いても構成される立方体は同じらしい。建築では平面図を用意するだろうが、絵を描くときに平面図を描く人は少ないのではないだろうか(設定資料などなら別かもしれないが)。3Dモデルの作成でも平面図を用いない人がいる(人間や自然といった複雑なものは直感的に作成したほうがうまくいくことがある)。
測点法(M点法)とはなにか、意味、定義、わかりやすく解説
測点法(M点法):測点を用いる透視図法のこと。
測点(Measuring Point,MP):追加の便宜的な消失点のような役割をする点の一種。特定の消失線上(主に水平線上)に位置し、透視図において物体の寸法を正確に測定するために用いられる便宜的な点のこと。
この点を使うと、物体の向きや位置に関係なく、実際の長さを透視投影を考慮して測定することができる。
介線法とはなにか、意味、定義、わかりやすく解説
介線法:介線を用いる透視図法のこと。
介線(medium line):傾斜角が45度の傾斜消失点に収束する直線のこと。測点(便宜的な点)の一種であると言える。この点を「介線点」と名付けることにする。測点と区別するため、略すときはMDPとする。
パースの用語や説明の難しさについて
さて、測点法や介線法の定義をきいたところで私はさっぱり分からない。また、解説している図を見ても、やはりさっぱり分からない。特に幾何学や数学などの理系的な要素が絡んでくると、文系である私は苦戦する。
たしかに手順に従って立方体を作ることは可能だが、「どうして可能か」について理解することは難しい(別の記事で扱いたい)。電車に乗ることは可能だが、電車がなぜ動くかについては知らないのと同じであり、あるいは知る必要もないのかもしれない。
「まずは二点透視図法で立方体を作れるかどうか」がパースを学ぶことを諦めるかどうかの分水嶺(わかれめ)となる。とりあえず試行錯誤を重ねていくしかない。「まずは描いてみる」という行為が重要だろう。
測点法で立方体を描く
奥行きを決める指標の点はいったいどこにあるのかという問題
立方体を描くためには「奥行きを決める指標」が必要だった。この指標が「測点(MP)」であることは理解できる。
では、その「測点の位置をどうやって決めるのか」という問題が生じる。
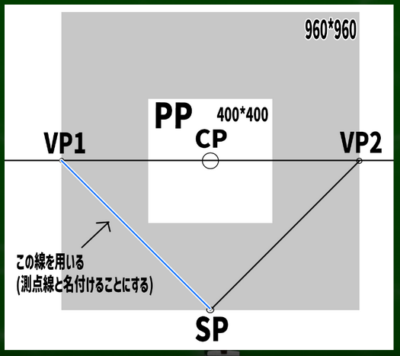
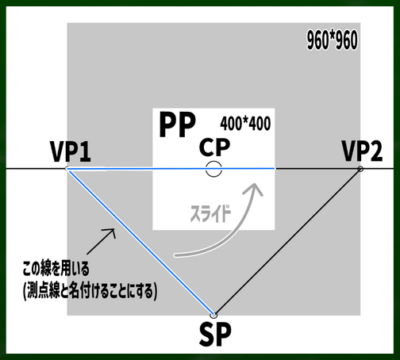
「測点線」を利用して見つける
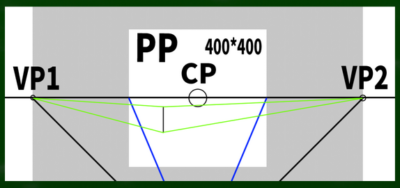
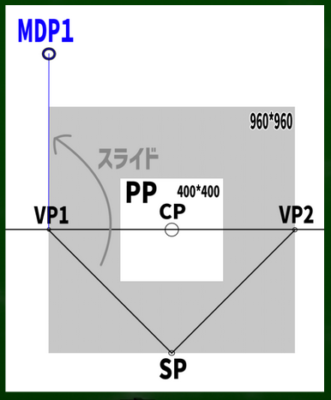
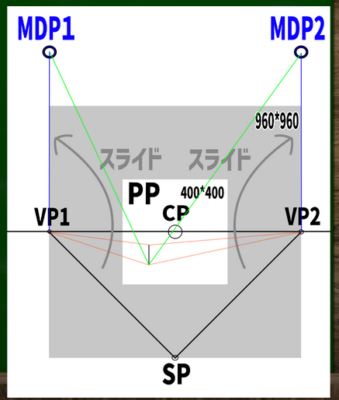
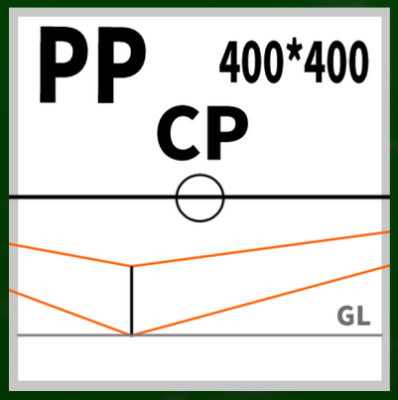
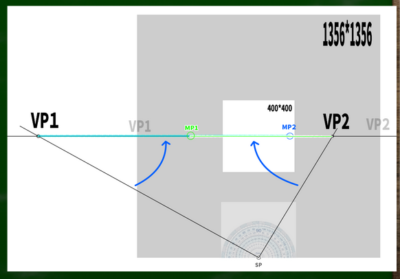
測点法ではSPからVPへ伸びる線を利用できるらしい。この線を仮に「測点線」と名付けよう。測点線を水平線上へスライドすれば、そこが測点だというわけだ。
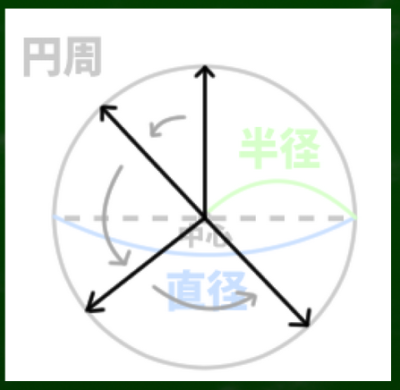
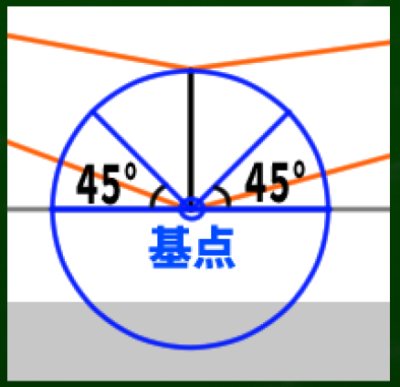
円周、半径、直径、中心などを学んで「スライド」を理解する
しかし「スライドとはいったいどういうことか」と頭の中に疑問が私には生じる。
「VP1を円の中心点だと仮定して、SPはその円の外周の点の一つだ」というのが私にはギリギリ理解できる説明である。
そもそも外周という言葉が適切かどうか、あやふやである。一旦学び直そう。
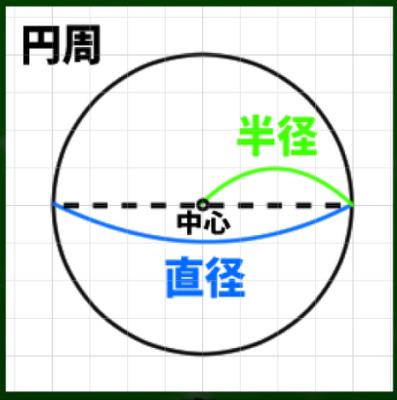
円に関するキーワードは「半径」、「直径」、「円周」である。小学生の時に、半径×半径×3.14(円周率)で円の面積が出ることを学んだ。
外周よりもここでは「円周」と呼んだほうが適切かもしれない。
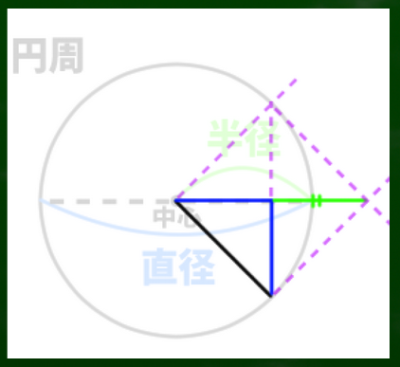
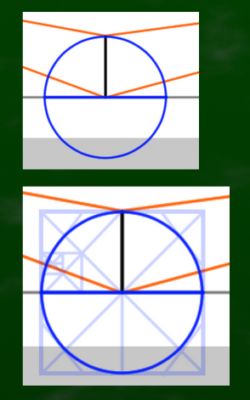
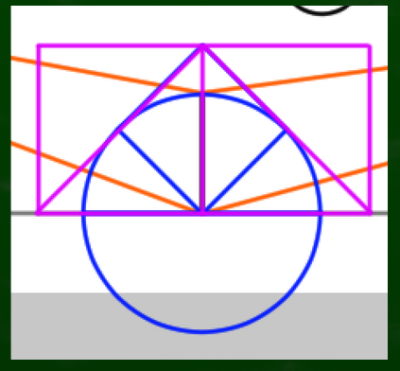
円の中心から円周へと伸びる線は多様に考えることができる。先程の図で言えば、このようになるだろう。
まるで時計の針が動くように、線がスライドしていくようなイメージができるはずである。それぞれの線が「(実測で)同じ長さ」だという点がポイントである。
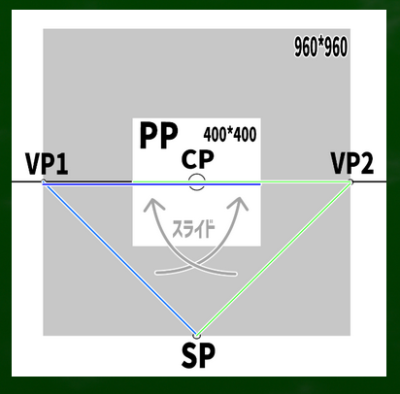
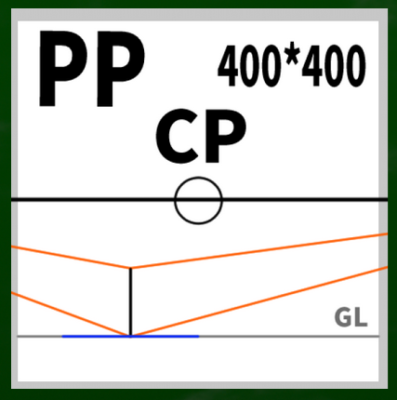
VP1を円の中心に見立て、SPへ伸びる線を水平線(HL)上にスライドさせるとこのようなイメージとなる。
※なぜ400*400の端にぴったりとMPがくるのか、という法則性には今回触れない
実際にどういう方法でスライドさせるのか
スライドさせるイメージは理解できたとして、「実際にどうやってスライドさせるのか」と疑問が生じるはずである。
※デジタルツールで変形すればいい、コピーすればいいという安直な発想はひとまずおいておこう。もちろんそれもアリだが、しかしそもそも論としてデジタルツールを使うなら最初からパースツールを作ったほうが早い。
まずアナログ的な手法として思い浮かぶのが、「物差しで測る」という手法である。円の中心から円周へと伸びる線がどれも同じ長さなら、直線を測り、その長さだけVPからCP側へ向けて線を伸ばせばいい。あるいはコンパスを用いてもいいかもしれない。これらは堅実な方法だろう。
あるいは頭の中で円をイメージするといったフリーハンド的な方法も考えられる。肘を軸としてコンパスにみたてる方法もある。あるいはシャーペンや鉛筆、ゴムやヒモ、自分の指を使って長さを把握したりするのもありかもしれない。
また、MPの位置はなんらかの法則によってキャンパスサイズから推測できるのではないか、すくなくとも汎用性のある数値を記録して使い回せるのではないかという考えも生じる。
これは後回しにする(違う記事で扱う)。
次に、幾何学的な手法によって可能ではないか、という考えも生じる。正直、文系の私ではよく思いつかない。正方形の対角線の長さが√2、つまり1.41くらいだと仮定すると・・・と考えてみたが、あまり実用的ではなさそうだ。
もちろん正方形を分割していって1.41へ近づける手法はあるが、物差しがないようなよっぽどの状態のときに使う非常手段のようなものだろう。
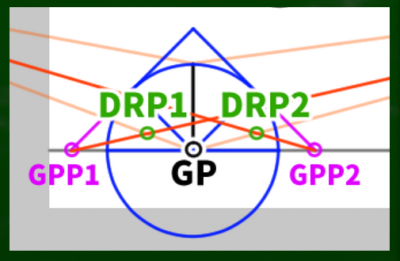
「奥行きを決める指標の点(DRP)」を使って奥行きを決める
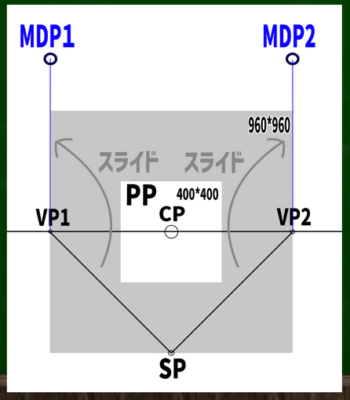
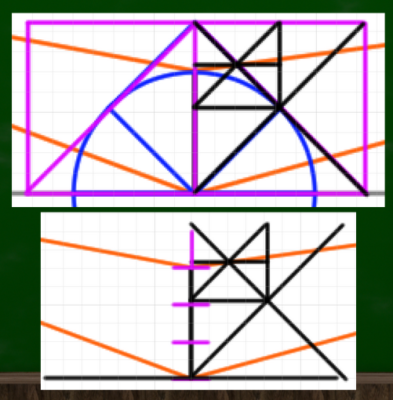
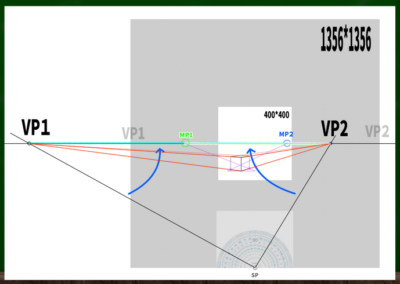
さて、これでスライドのやり方がわかった。VP1とSPの測点線と、VP2とSPの測点線を両方スライドさせていくと、2つの測点を発見することができた。
さて、これをどう使って奥行きを決めるのか。
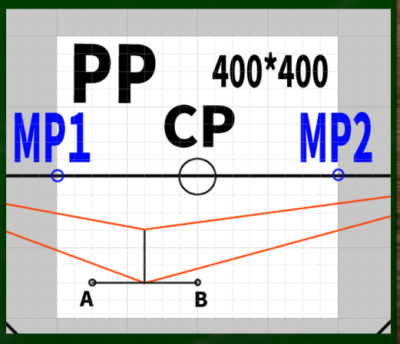
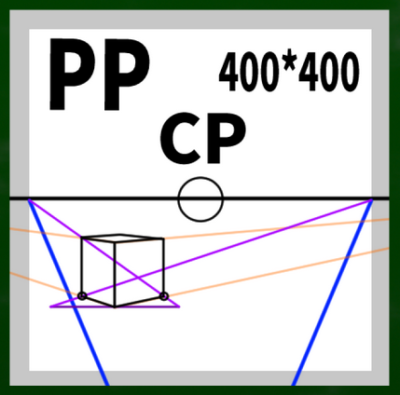
(1)描きたい立方体の垂線を引く
 (1)まず、適当な垂線を引いてみる。自分が描きたい高さの立方体をイメージすればいい。
(1)まず、適当な垂線を引いてみる。自分が描きたい高さの立方体をイメージすればいい。
(2)垂線の点からVPへと線を伸ばす
(2)頂点をVP1やVP2へ、つまり本来の消失点へ伸ばしていく。もちろん、この段階では奥行きがわからない。
(3)垂線と同じ長さの線を左右に引く
これも、物差しで測るほうが正確だろう。斜線を平行線に戻すわけではないので、フリーハンドでも引きやすいかもしれない。あるいは45度に線を伸ばしていけばそれぞれの点と接触する。
それぞれの頂点をA、Bとしておく。
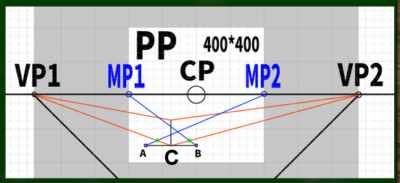
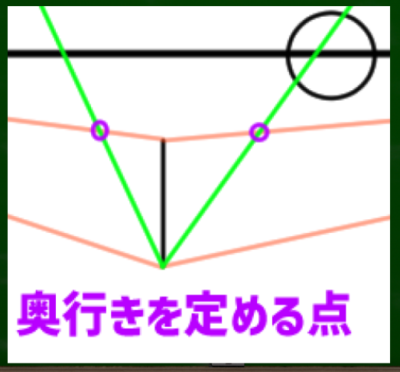
(4)【奥行きを決める点(DRP)の発見】AをMP2へ、BをMP1へと交差するように伸ばしていく。
最初に引いた垂線の下の点をCとする。「AからMP2へ伸びる線」と「CからVP1へ伸びる線」が交差する点が「奥行きを決める点」である。反対も同じように決める。
(5)後は立方体を完成させるだけ
「奥行きを決める点」から線を伸ばしていけば立方体ができる。
残りの線もVPへと伸びる線を使って形成していく。
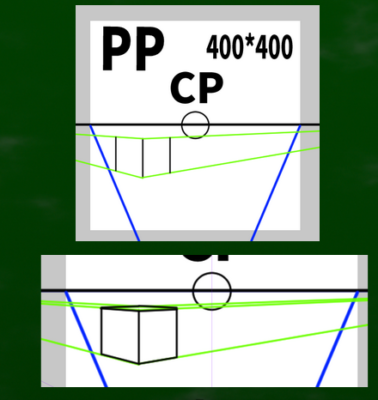
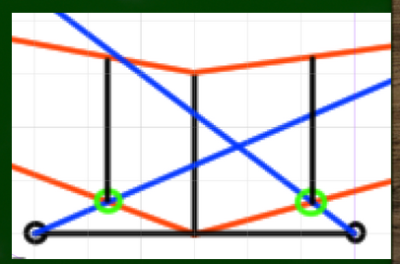
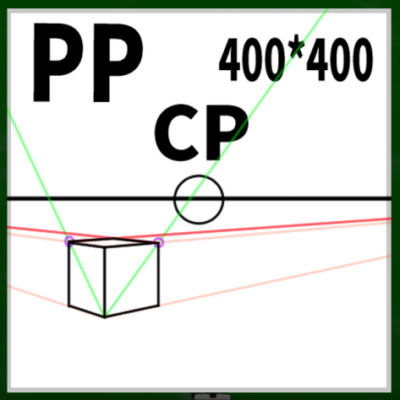
完成した立方体
完成した立方体はこちらである。違和感はほとんどない。
このやり方で一番重要なのは測点の求め方であり、それがわかればあとは簡単である。
介線法で立方体を描く
介線とはなにか、意味、定義、わかりやすく解説
介線(medium line):傾斜角が45度の傾斜消失点に収束する直線のこと。介線の先にある点が45度消失点であり、測点(便宜的な点)の一種であると言える。この点を「介点」と名付けることにする。測点(MP)と区別するため、略すときはMDPとする。
介とは一般に「間にはいる、なかだちをする」といった意味がある。「仲介」などという言葉を聞けばわかりやすい。
とはいえ、いったいなんの中間をしているのか、よくわからない。媒体という意味合いで使えば、奥行きを調べるためのなにかの手段や道具と解釈できる。
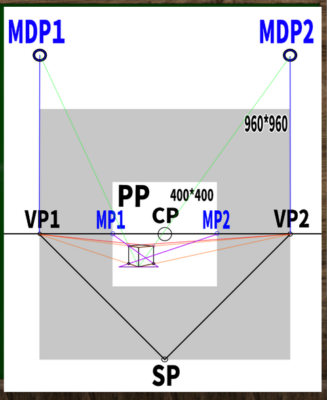
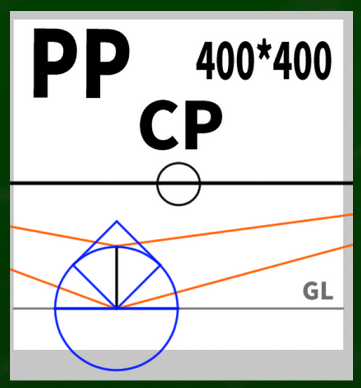
まず、この画面までは以前の動画までの知識で構成できる。介線法で主要な問題は「奥行きを決める介点がどこにあるのか、どうやって定めるのか」である。
さきほど測点法で習得した「円周を用いてスライドさせていく方法」を理解していれば簡単である。
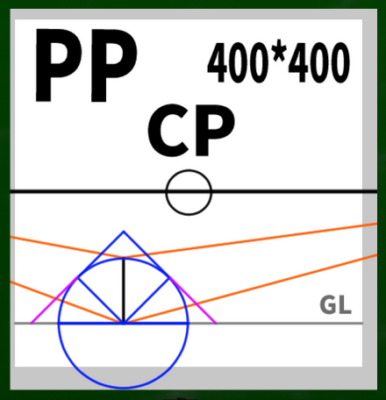
(1)介点を定める
SPからVP1への斜線と同じ長さの線をVP1から垂直に伸ばしていけば、そこがMDP1となる。
物差しやコンパスを使ったり、デジタルで変形やコピーを利用してもいい。もちろん直感で引いてもいい。VP1からCPの長さを1とすれば、√2(1.41)の長さである。480 ×1.41 = 676.8であり、キャンパスサイズでいえば1353×1353。
反対側も同じようにMDPを定めていく。左右均等の角度の二点透視図法なので、基本的に同じ高さにくる。
(2)任意の垂線を引く
自分が作りたい立方体の高さの垂線を引いていく。
(3)VPへと垂線から線を伸ばしていく
(4)MDPへ垂線の下の点から線を伸ばしていく
(5)奥行きを定める点(DRP)を定める
(5)VPへと伸びる線とMDPへと伸びる線が交差する点が「奥行きを定める点」である
※この奥行きを定める指標の点を「DRP(Depth Reference Point)」と略しておく。
(6)後は立方体を完成させるだけ
完成した立方体
完成した立方体はこちらである。違和感はあまりない。
測点法と難易度はそこまで変わらない気がする。ただし、作業スペースがより多くいるのかもしれない。
測点法と介線法は一致するのか
検証
さて、ここで疑問が生じる。測点法と介線法で「同じ立方体」が構成されるのかという疑問である。検証していこう。
介線法でつかった同じ長さの垂線をまずは用意する。そして測点法を使って立方体を形成したものがこちらである。
もう一度先程の介線法で立方体を見てみる。どうやら同じような立方体ができてそうである。
検証結果
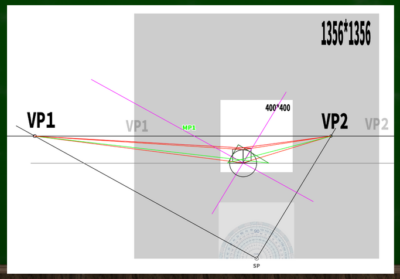
重ねてみるとこのようになる。
検証結果は「測点法と介線法で作った立方体は一致している」ということになる。
基線法で立方体を描く
基線とはなにか、意味、定義、わかりやすく解説
まずは基線とはそもそもなにかを理解していこう。
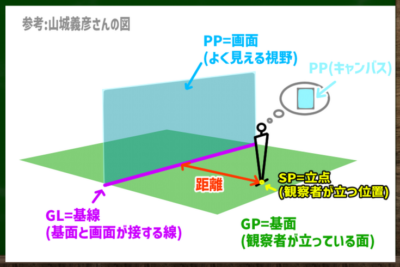
基線(Ground Line,GL):基面と画面が接する線のこと。
基面(Ground Plane,GP):対象物が置かれ、見る人が立っている面
画面(Picture Plane,PP):描いている視野を(たいていは)長方形に切り取ったもの。
画面内の基線はどこにあるか
基線の定義を説明されても正直、私はよくわからない。
こういうときは図にするといいと聞いたことがある。
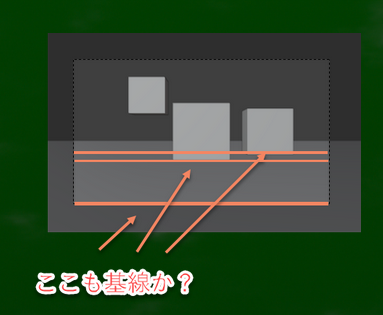
例えば目の前に立方体が3つあるような状況を考えるとする。右のような図である。さて、この画面内の基線はどこにあるか。
さっぱりわからない。そもそも透視図内にGLというものが存在するのかすらわからない。
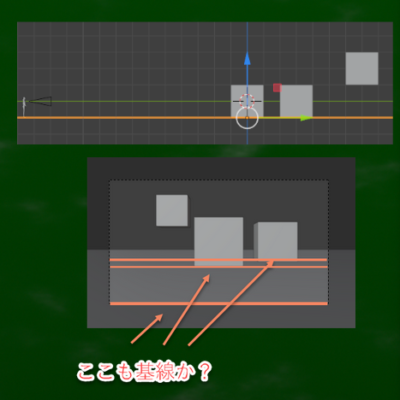
たとえば真横から、平面図として見れば、このオレンジ色の線が「基面」である。
真上から見ればこのオレンジ色の面が「基面」である。具体的に言えば観察者から見た地面のことである。
さて、基面と画面が一致するとはどういうことか。たとえば最初に見せた画像が、画面そのものである。
これと基面が一致するところとはどこか。
私はPPの一番下が基線、つまりGLだと思っていた。
しかしほんとうにそうだろうか。画面(PP)と基面(GP)が交わる点は他にもたくさんあるのではないか。
たとえばここも、あそこも画面と基面が交わる線だと言える。
画面が枠だけである論理的な理由はないはずである。画面とはあくまでも窓のように、その全体を意味するはずである。
要するに、横からみると一本の線のように見えるが、前から見るとたくさん、無限のようにあるのではないだろうか。もちろん地球は丸いので厳密には直線ではないかもしれないが、短い範囲ではほぼ直線だろう。
基線法を平面図を用いずに描いていく
さて、基線法とは文字通り「基線」を利用する透視図法のことである。
測点法と介線法は平面図を利用せず、足線法と基線法は平面図を利用するという区別を以前行った。しかし、どうやら基線法は平面図がなくともいけそうだ(単純な立方体だからできるのかもしれないが)。
(1)描きたい立方体の垂線を描く
これは任意のサイズであり、自分が決めていい線である。検証のため、いままで測点法や介線法で利用した位置と長さにした。
(2)各VPへ線を引く
(3)基線を引く
立方体が地面の上にあると仮定し、一番手前の頂点を通る線をGLとしていく。
(4)引いた縦の線と同じ長さの横の線を左右に引き、円をつくる
円を正確にアナログで引くためには、まずはコンパスを使う方法が有効だろう。今回はコンパスを使ったと想定する。
コンパスがない場合は正方形を作り、正円を近似するという面倒な方法がある。建築のような精密さが絵に毎回求められるわけではないので、直感的に引いてもいいのかもしれない。もちろん、デジタルの場合は素直に円ツールを用いればいい。ちなみに実際に使うのは上半分の円だけなので、半円でもいい。
(5)SPからVPへと伸びる線と平行な線を基点から各VPへ伸ばす
ここがいまいち理解しにくいポイントだろう。今回のケースは二点透視図法の90度、かつ左右均等(45:45)のケースである。つまり、左右に45度の角度で伸びている。それゆえ、45度の線を基点から伸ばしていけばいい。
線を実際に伸ばしていくとこのようになる。
もし違う角度の、たとえば30°:60°のケースだとすれば、分度器を使わないと難しいかもしれない。あるいは幾何学的な方法を利用する必要がある。
(5)左右に伸ばした線を基準に正方形をつくる
これは簡単だろう。特に今回は45°なので、斜線を引いていけば正方形が完成する。
(6)正方形の線を延長する
三角形を作るようなイメージで、正方形の辺をこのようにGLまで延長する。
あるいは対角線(√2)を用いて大きな正方形を想定してもいいのかもしれない。
ところで、かなり雑な近似でいいとしたら、ショートカットできる方法があるかもしれない。この方法だと正円を描く必要はない。
たとえば最初の垂線を1として、その1/3を足して正方形をつくるという方法である。もちろん実測ではもうすこし大きい。おそらく1/3+1/12(1/3 の1/4)くらいだろうか。今気づいたが1/3+1/12は5/12であり、およそ0.41である。つまり全体としては1.41となり、ほとんど√2と同じ値である(差は約 0.0027)。
(8)新しく定まった点からVPへと線を伸ばす
新しく定まった点を仮に「基線点(GPP)」と名付けることにする。GPP1はVP2へ、GPP2はVP1へと線を伸ばしていく。
GPPからVPへ、GPからVPへと線を伸ばしていき、その交点が「奥行きを定める指標の点」となる。
この奥行きを定める指標の点を「DRP(Depth Reference Point)」と略しておく。
(9)立方体を完成させる
後は、DRPに従って線を引くだけである。
立方体だけを表示させるとこのようになる。
「測点法や介線法」と基線法は一致するのか
検証結果
上の図の通り、一致している。どの方法を使っても同じ立方体が、今回のケースではできる。
他の視円錐や角度を試す
30:60ケースを試す
今までの透視図法は主に二点透視図法の90度視円錐の45度均等のケースだった。今回は不均等のケースを扱ってみよう。たとえば左に30度、右に60度のケースである。
前提画面を作る
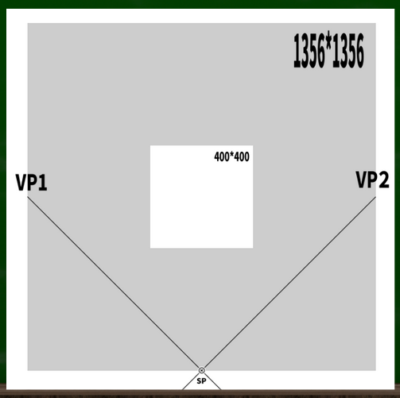
キャンパスサイズは簡単な400*400にしておく。視円錐で画面を覆い尽くす場合を今回は採用する(全部ケース)。
※そのため、計算式はX(正方形の一辺)=√幅の二乗+高さの二乗となる。計算すると、565になる。この数値に2.4を掛ければいい(45度視円錐)。計算すると、1356となる。なぜこのような計算式を用いなければならないか、視円錐を考慮せねばならないかについては第四回の動画を参照してほしい。もっと簡単で妥当な方法があるかもしれないが、現状ではこの方法をとる。
【第四回】パースの基礎を学ぶ:パースにおける視円錐とはなにか、その設定方法
図にするとこのようになり、VPから90度に線を伸ばすとSPが自動的に定まる(VPを定めたらSPも決まる、その逆もしかり)。
しかしこのままでは左右45度均等の透視図法になってしまう。
左に30度、右に60度に分配する方法
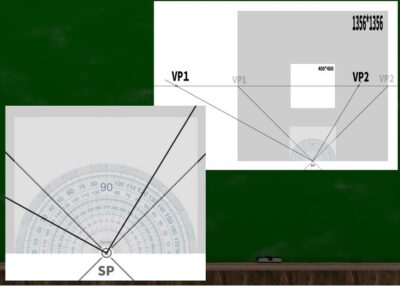
さて、左に30度、右に60度に分配したいときどうすればいいのか。
今回は素直に分度器を使う。※なんらかの法則性を用いて分度器を使わなくてもできるのかもしれないが、今回は動画が長くなりすぎてしまったので別の機会に繰り越す。
測点法で試す
まずは測点法を試そう。
(1)まず、SPからVPへの線をそれぞれスライドさせる
(2)あとは学んだ手順通り、立方体を形成していく
45:45と30:60を比較してみる
やはり、明確な違いがわかる。30:60のほうが左の面の範囲が大きくなっている。どちらが美しいか、これだけでは容易にわからない。顔をよく見せたい場合は、顔の範囲が多いほうがいいだろう。つまり、より上位の文脈(コンテクスト)によってより下位の関係の在り方が定まり、その要素の在り方が定まるということになる。
介線法で検証
一応、介線法と基点法もそれぞれやって一致するか確かめてみた。まずは介線法がこちら。
基点法で検証
基点法はこちら。やはり45:45以外は、描くのが少し面倒な気がする。
検証結果
いずれの方法をとっても、おおよその位置が一致することが判明した。
測点法が比較的楽かもしれない。他にも90ではない、たとえば60:60や30:90のパターンも応用することができる。いずれにせよ90のパターン、特に45:45が作りやすそうだ。しかし見せたい角度、美しく見せる角度を第一に考えたほうがいいだろう。
次回の予定
・三点透視図法とは何かを説明する予定
参考文献
初心者でもわかりやすい本
ロビー・リー「超入門 マンガと図解でわかる! パース教室」
・パース全般の基礎において一冊目にこれを手に取るのに適している。 ・私は「パース!マンガでわかる遠近法」よりも平易に、かつ丁寧に説明されていると感じた。それゆえに、初心者は特に一冊目にこの本をおすすめする。
デヴィッド・チェルシー「パース!マンガでわかる遠近法
・イラストが多く、わかりやすい。パースの基礎用語の説明もされていて、かつ平易にパースの使い方が説明されている良本。ただし、建築パースに特化しているわけではなく、「イラストレーション(漫画)」に特化している点を注意する必要がある。 ・パース全般の基礎を学ぶという目的において一冊目にこれを手に取るのに適している。
上級者向け
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
絵を描く、特に線画に特化した本。小難しいが広く、深く説明されている良本。
山城義彦「現代パースの基本と実際」
・パースの歴史や細かい用語が説明されていて便利。ただしメインはイラストレーションではなく「建築パース」に特化している点を注意する必要がある。 ・かなり小難しく説明されている(建築パースゆえにそうならざるをえないのだろう)。例えるなら文系が理系の数学を見たときのあの感覚に近い。建築家ならば通らなければならない道ではある。ただし、この本はだいぶ古く、現代ではコンピューターグラフィックスをもっと多用して楽をするのだと感じた。ただし、楽をするにもその原理を知っておいて損はない。
その他
参考サイト:パースフリークス(URL)
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
・全般的な絵の知識が語られている本であり、パースに割かれる箇所は少ない。ただし、それなりにそれぞれ濃く説明されている本である。 ・パースを学ぼうとしてとる本ではないが、絵の描き方を学ぼうとする場合は選択肢に入ってくる。ただし高いのが難点。
コメント
この記事へのトラックバックはありません。




















この記事へのコメントはありません。