平行投影とは?
図法幾何学を学ぶ意味と問い
武道家は縄跳びで体力をつけることがある。しかし実際の戦いで縄跳びを使うことはない。
私にとって図法幾何学を学ぶことは「縄跳び」に近い。武道家は体力をつけるたびに縄跳びをするが、「空間把握能力」を身につけるために図法幾何学を学ぶ意味があるのではと思った。空間把握能力は絵を描く人にとって武闘家の体力に相当するものだと思う。あるいは相手との距離のとり方の練習でもなんでもいい。
空間把握能力がなくても絵は描ける。しかしあったほうが幅が広がると思う。なぜ自分の絵は美しくないのか、と壁を感じた場合の解決法の一つに自分の基本的なスキルを磨くという手段がある。
図学を学ぼうと思ったきっかけはblenderで平行投影と透視投影という用語が出たことにある。理解しないでもきっとblenderは使っていける。しかしもどかしい。理解したいと思った。
私は絵描きではないし、図学を実務として仕事で使う建築家でもない。そうした人たちが絵を学ぶときにつまずいた時、ショートカットできるような道筋を建てたいと思い記事を書いている。
絵を描くことが目的なはずなのに、調べることばかりで技法にこだわりすぎて絵を描けない人(私のような人)もいる。そういう人たちの調べる手間を省けるように道筋を残したい。
ここまで大言壮語したはいいが、図学はかなりとっつきにくい分野だ。透視図法(パース)も同様にとっつきにくいが、図学も同じくらいそうだ。
ほんとうは平行投影と透視投影を同時に解説し、その違いについて解説しようとしたのですが、2つにわけることにしました。というより透視投影がかなり難解なので後回しにします。
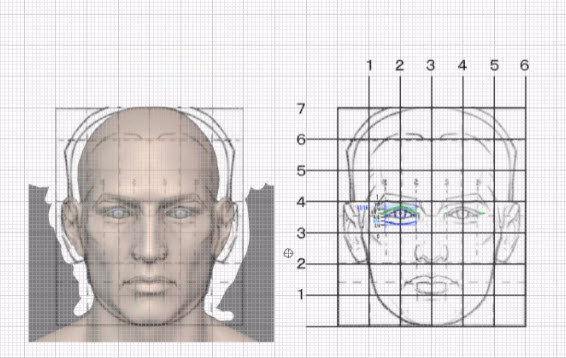
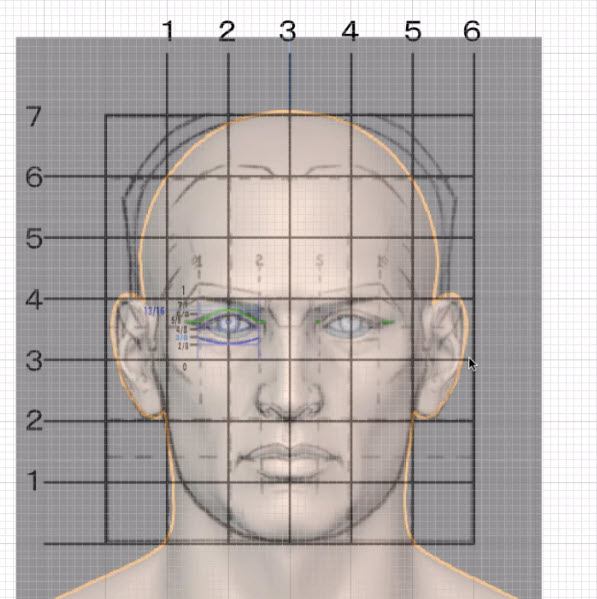
私の直接的な理由は「ルーミスの顔は実は平行投影的で、自然ではないのでは?」という疑問に対する解答のための学習です。ルーミスの顔を見ていて、あれ、これ他の頭部に比べて大きすぎないか?と思うことが多々ありました。個人差(あるいは当てはめのミス等)があるので「ヨソハヨソ」と済ませる方法も思案しましたが、モヤモヤがあると前に進めないタイプなので学びます。
図面の果たす役割
「図面の描き方が優しくわかる本」(西村仁)では図面の果たす役割を以下のように示している(20P)。
1:頭の中で考えたことを、誰もが見えるように描き出すこと
2:描き手の意図を、読み手に確実かつ容易に伝達すること
3:情報を保存すること
なるほど図面にはそういった役割があるのか。絵の分野でも仕事の依頼を受けて、キャラクターの三面図を求められることがあるだろう。そこでもやはり自分の考えるキャラクターのイメージを正確に伝える手段や、他の人が動かすための情報としても有用になってくるのだと思う。
ただし、消しゴムやホチキスなどの工業用品と違い、人間はかなり複雑だ。はたしてこれから学ぶような工業的な平行投影が役立つかどうかはわからない。
平行投影を頭の中でパースと結びつけて、自然な絵を構成できるスキルというものがあるのだろうか。最初から透視投影を描けばいいのだろうか。あるいは両方なのか。なかなか難しい分野に頭を突っ込んでしまった。
欠点1:見えない面に加工があれば、追加の立体図が必要になる
欠点2:斜め線が多くなり、描きにくい
欠点3:立体図に寸法などの情報を書き込みにくい
欠点4:見えない面への表面粗さ情報などが記入できない
同じ本の中に、以上のような立体的な絵の弱点も書いてある(51P)。とはいったものの、一般的な人が絵を描く際に、このようなことは気にしない。つまり投影法について深く学ぶ理由はないのではないか?という考えが頭をよぎる。しかし空間把握能力、論理的思考能力、図形把握能力等々を鍛え、さらに遠近法(パース,透視図法)を理解するための前提知識にもなりうるのではないか?という考えも頭によぎる。blenderでも投影法を使ったカメラのテクニックがあるそうだ。興味深い。
結果的に、ざっと浅くてもいいので学ぼうと思いました。実際CADや3dcgソフトで簡単にできてしまうことも多いので、使わなそうな技法や数学的な側面へはあまり深入りせずに行こうと思います。とはいっても簡単な数学には触れたいと思います。
絵を描くために必要な図学の知識とは?という視点の記事のため、建築設計で必要な知識とはすこし違うかもしれません。
角度
絵を描くための角度感覚について
まず基礎体力として使えそうなのが「角度」を気にすることである。模写でもそうだ。この線とこの線の関係は30°くらいだな、と頭に入れて描くと意外とうまくいったりする。角度の感覚は絵の上達方法の一つに入れてもいいと思う。プロ野球選手が投げる場所を細かく定めるように、絵を描く際も角度を意識してみるといいかもしれない。
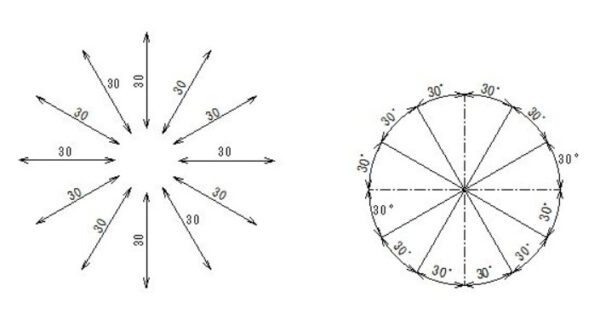
15°単位にするか、30°単位にするか、幅は自由に設定していいと思う。細かいほど正確になるが、細かすぎると頭がパンクしてしまう。
しかし角度はどのように考えたらいいのだろうか。分度器だろうか。cadではマイナス45°という概念もあったりする。右側が45°なら、左側のマイナス45度に相当する角度は135°になる。そもそも右側が135°と書いてある分度器もある。角度は面倒だ。この項目では図学というより、角度について絵に通ずる面を考える。
分度器には半円分度器と、全円分度器の2つが主にあるそうだ。右下斜45°と伝えたい時の角度を考えると・・360°と270°の中心は・・・315°ですね。右下斜45°に線を引いてください!と伝えるのと、315°に線を引いてください!はどちらが伝わりやすいのだろうか。あるいは図学ではどのように伝えるのが正しいのだろうか。
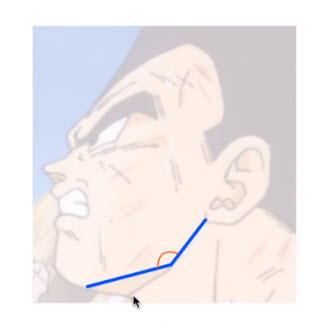
さきほどのベジータさんの線の角度の話に戻ろう。このベジータさんの角度は145°である!という答えは正しいのだろうか。
たしかに間違っていない。ただ直感的ではないような気もする。
たとえば135℃の角度がある線を描いてくださいと言われて上記のような線はほぼ描けないだろう(?)。描けたとしてもわかりにくいし、直感的ではない。もっとも線を構成するためには角度だけではなく、長さも必要だ。これは相対感覚の記事で扱おうと思う。
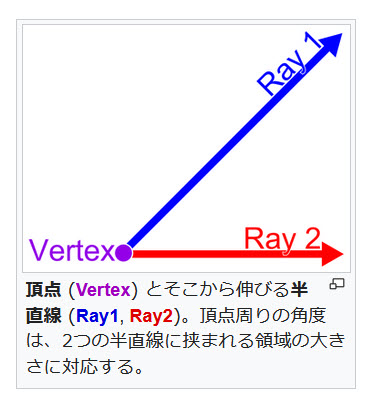
角度はそもそも頂点とそこから伸びる直線によって形成されている。頂点を英語でvertex、線を英語でrayという。
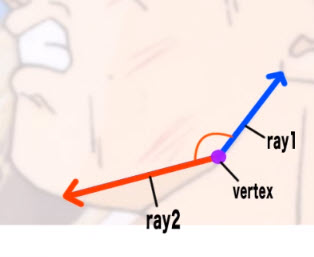
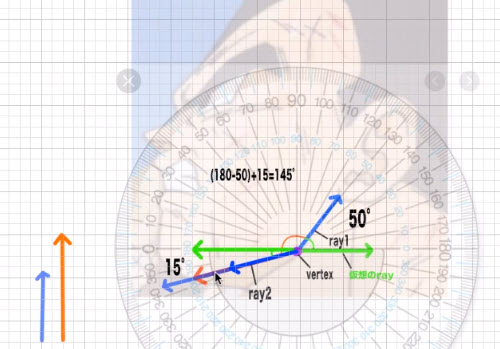
今回のベジータさんの線をこのように当てはめてみました。
ray1とray2からなる角度が145°の大きさであることはわかります。しかしそれだけでは使えません。rayが完全に水平、あるいは垂直であればわかりやすいのですが、今回はそうではないのです。ちなみにこのような角度を鈍角といいます。
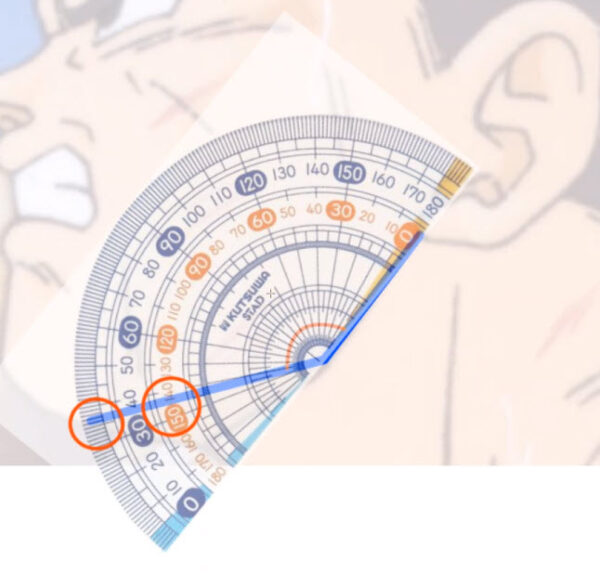
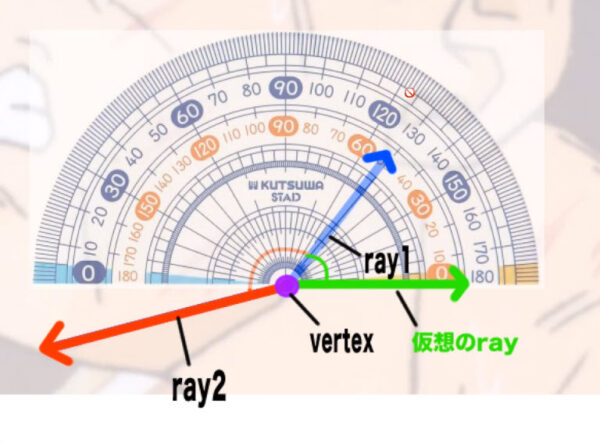
さてまずra1でもray2でもいいのですが、その角度を求めていきます。この仮想のrayは用紙や画面に対して平行な、真横の線である必要があります。この仮想のrayとray1からなる角度の大きさは50°です。別の言い方をすれば、rawは右上に50°伸びている線という言い方ができます。
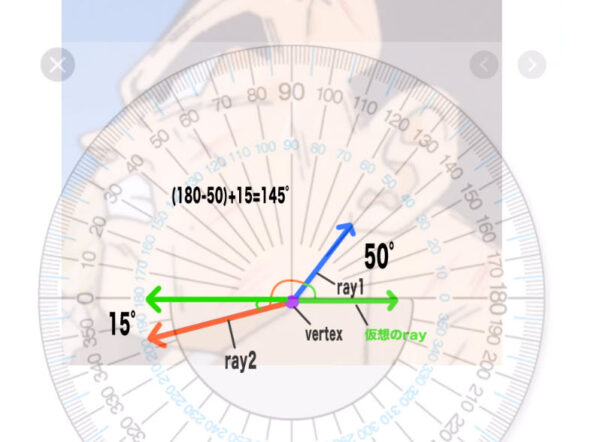
ray2でも仮想のrayを用意します。仮想のrayとray2からなる角度の大きさは15°です。別の言い方をすれば、左下に15°伸びているという言い方ができます。もしray1とray2の角度の大きさを計算するとすれば、(180-50)+15=145°です。
もし相対感覚を使って線を把握するとしたらどうなるでしょうか。ray2はray1の何倍でしょうか。斜めに伸びる線は難しいですよね。ray1が3だとすれば、ray2は5くらいです。つまり5/3倍なので、1.66倍くらいになるわけです。頭の中でray1を10分割して、まず半分を伸ばします。これで1.5倍です。そこから1.6を付け加えるとすると・・・半分の線の2/5で1.7だから・・とややこしい。他にいい方法があるのかもしれないが、これは本来デッサンで繰り返し磨くスキルでもあります。
絵の巧さのひとつに目で見たものを描くというスキルがあるのですが、その際にこの角度感覚と相対感覚は必須スキルになるのではないでしょうか。天才肌の人はなんとなくできてしまうし、努力家の人はデッサンの積み重ねで空間把握能力や相対感覚を身につけていると思います。天才でもないし努力家でもない人は私のように(大袈裟な言い方かもしれませんが)論理的に線を形成するほうがむいているのかもしれません。
あるいは論理的に線を形成する意識を頭の隅にいれながら、何度も努力してデッサンを行うというハイブリット型もいいのではないでしょうか
図学における角度
いわゆる「角度寸法」というやつです。-30°とか、120°とかそういう言い方をしないんですね。
図学では基本的に角度は度(°)であらわすそうです。円の一周を360°とする単位です。1°の1/60の単位を1分、1分の1/60の単位を秒で表すそうです。度以外にラジアンの単位で表すことがあるそうです。
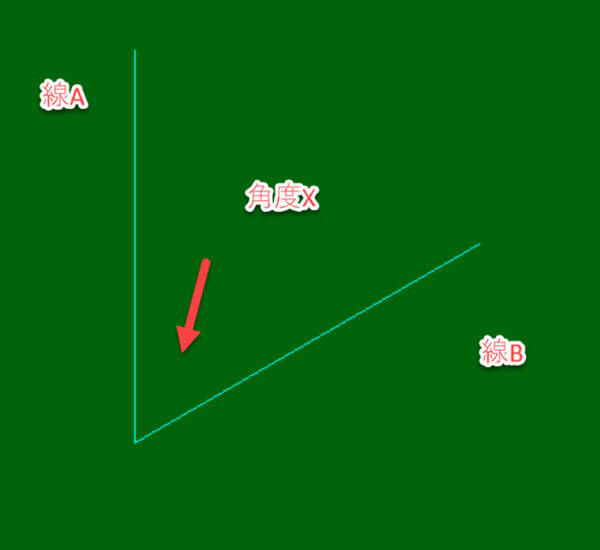
例題1:この線は何°の大きさか?線Aと仮想の平行線からなる角度の大きさは?線Bと仮想の平行線からなる角度の大きさは?
60°,右上に30°,真上に90°, 90-30=60°
投影と作図
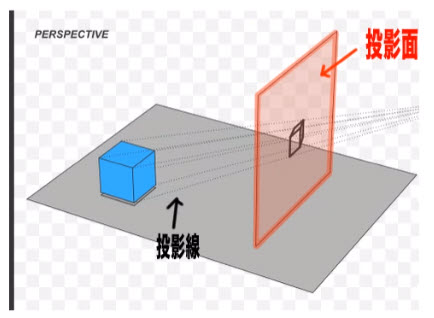
投影(とうえい,Projection):三次元の形を二次元平面上の映し出す操作を投影という。投影された面を投影面という。投影面上のかたちを紙面に表現することを作画という。
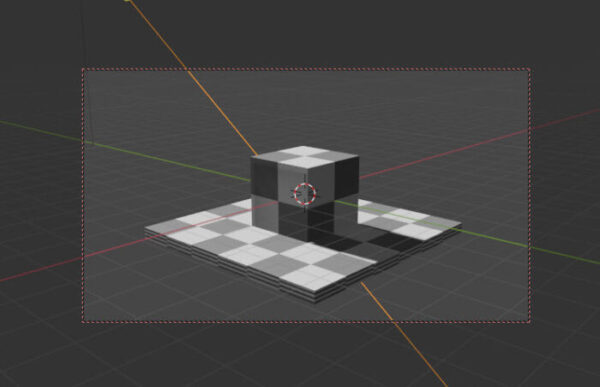
Blenderでカメラを操作する時に、枠のような物が出る。透視図法ではPP(画面)といわれる枠だ。カメラの用語で言えばファインダーだろうか。
これが投影面といっていいのだとおもう。立方体をどのような角度から投影させるのか、どれくらいの距離で投影させるのか、平行か、透視かといった問題が次に出てくる。
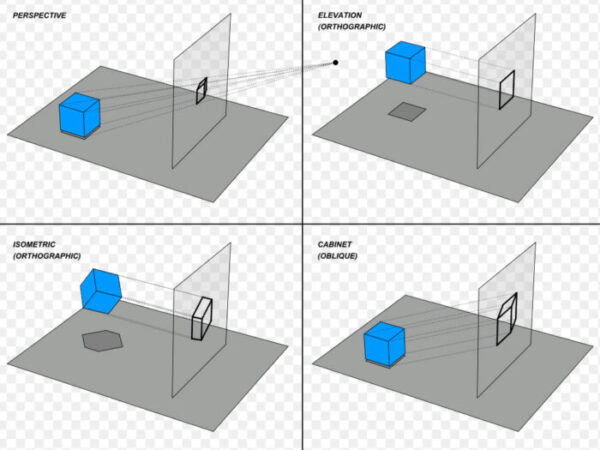
WIKIの画像を借りてみました。これが投影面なんですね。透明の四角い定規を立方体の前に合わせているようなイメージでしょうか。
平行投影とは
平行投影とは
平行投影(へいこうとうえい,Parallel projection):平行投影は、投影方向を定める線(投影線)が、すべて並行となる投影方法。平行投影は垂直投影と斜投影に分かれ、さらに垂直投影は正投影と軸測投影にわかれる。
何を言っているかわからない。初めて何かを学ぶ時は、往々にしてそういうものである。私も今書いていて、さっぱりわかっていない。
とりあえず平行なんだな、ということはわかった。
blenderにも平行投影、透視投影という用語がある。実際に試してみよう。
まずは透視投影のレンダリング。
次は平行投影のレンダリング。
同じ画面なんですが、わかりにくいですね。しかしよく見れば大きな違いに気づきます。
そうです、平行投影の場合は大きさが奥へ行っても変わってないのです。
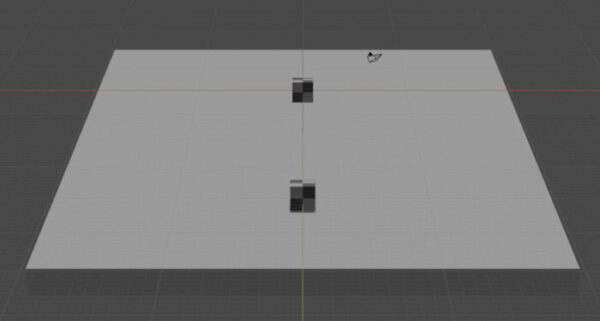
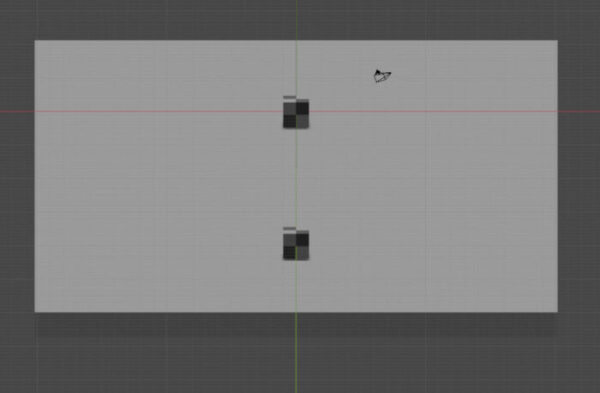
もう一度違うオブジェクトで比較してみます。
透視投影のほうは奥にいけばいくほど小さく、短くなっていきますが、平行投影の方は同じ大きさです。
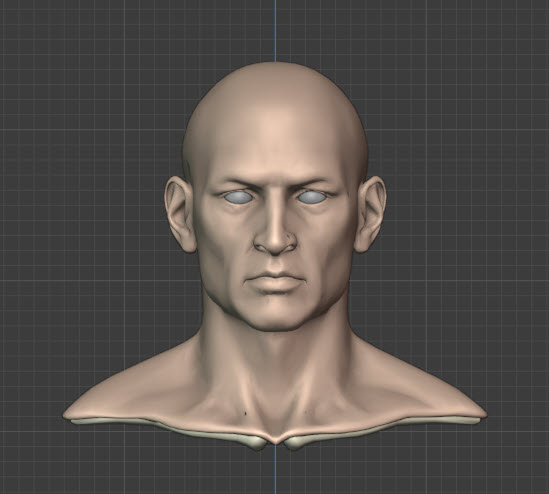
更にわかりやすいものを見ていきましょう。動画だとわかりやすいです。今度は人間で試します。透視投影と平行投影を繰り返し切り替えているだけです。
透視投影の場合は近くにあるものが大きく、遠くにあるものが小さく見えます。
人間の頭部の場合は目鼻のほうが近くにあり、側頭窩は遠くにあります。したがって透視投影のほうが眼や鼻が大きく、側頭窩付近が小さく見えるのです。平行投影の場合はそうした差をつけずに均一に扱います。
美に関する問題だと、どちらのほうがいいのでしょうか。人それぞれで済ませるのは簡単ですが、ここを熟考するべきだと思います。一般的には透視投影のほうが人間の目には自然に見えるようです。
美しいと思えるような視点を探すのも楽しいと思います。より写実的なものを目指すのか、人工的なものを目指すのか、折衷か、あるいは第三のものか、たくさんあると思います。
とはいえ平行投影は基本的には工業分野で使うような印象があります。blenderも作業中に「実際の長さは同じなのに見え方が違う」と作業しにくいので平行投影に変えて編集するといったことをよくします。
机の設計図で透視投影がつかわれていると、手間と奥じゃ長さが違う板なのか?と勘違いされてしまうかもしれません。定規で図っても同じ長さになるのが平行投影です。
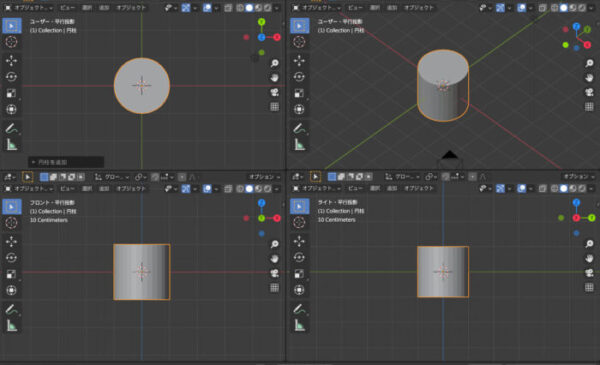
円柱の場合もわかりやすいですね。平行投影の正面から見た形は、ほぼ直線ですよね。長方形のような形をしています。
やっぱルーミスの顔はでかいんじゃねーかと再度思う私です。
正投影
正投影(せいとうえい,Orthographic projection):対象物を投影面に対して垂直に投影する方法。対象を90度ごとに回転させるか、または視点を90度ずつ回転させて、複数の視点から描画された図。建築、工学、デザインなどで用いられる。物の形状を正確に表すことができる長所がある。平行投影は垂直投影と斜投影に分類でき、正投影は垂直投影のひとつである。
この辺からすこし私の頭はくらくらしてきます。
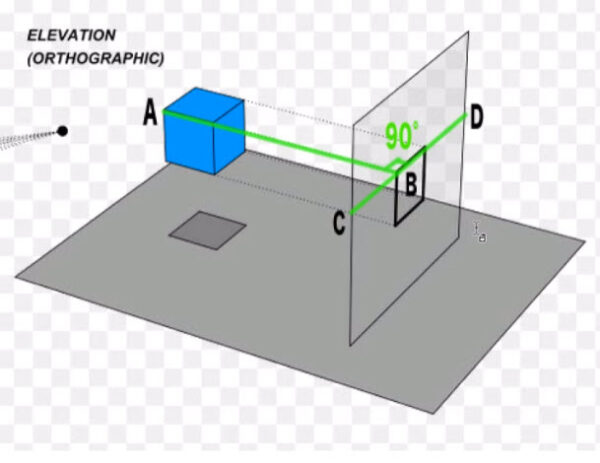
右上のELEVATIONが正投影ですね。
たしかに立方体から投影面にかけての線(投影線)がまっすぐですね。
まっすぐというといろいろややこしいです。垂直に伸びてますね。
垂直という言葉もややこしい。投影面をCDと仮定すれば、たしかにABにあたるような線が伸びていますね。垂線であるということは、角度が90°ということになります。
また透視投影とは違って、投影面に一つの面しか表示されていませんよね。ひとつの面というのが、このケースでいうと「正面」になるわけです。この面について次の項で学びます。
第三角法とは
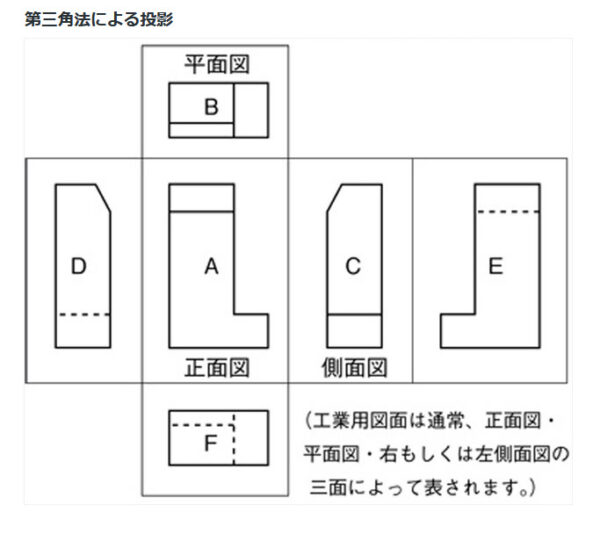
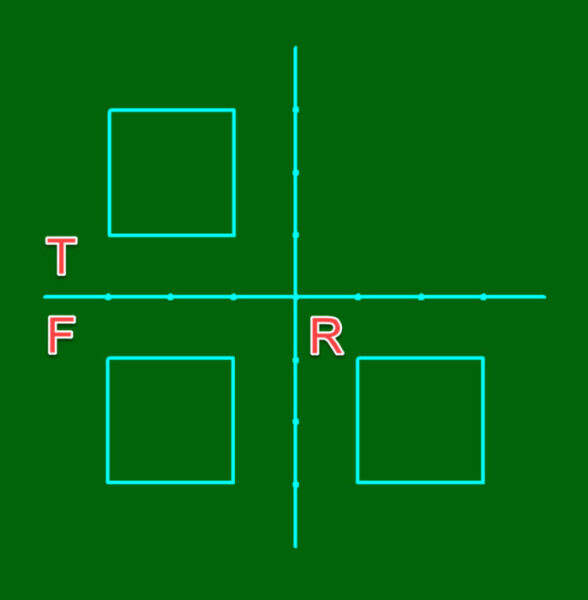
第三角法(だいうさんかくほう,Third Angle Projection):垂直及び水平な投影面に、対象物の形状を投影する作図法。正投影法のひとつ物体を第三象限内の空間において作図することに由来している。通常は正面(F)・平面(T)・側面(R or L)の三面図で構成される。この三面図を主投影図という。第三角法において三面図を作成する際は、物体の最も代表的な面を正面図として書き込む。
とりあえずそれっぽいものを本を参考に作ってみました。実際は破線が入るので同じではないですが、イメージはしやすいです。
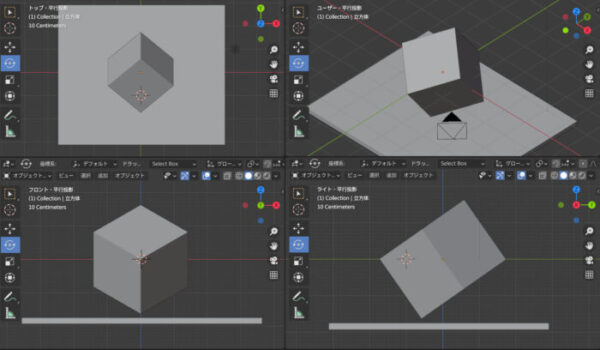
3点のどの方向から見ても長さに遠近感がないので、絶対値としてグリッドが使えるということでしょうか。右上は三面図とは違いますが、余ったので斜めからみてみました。
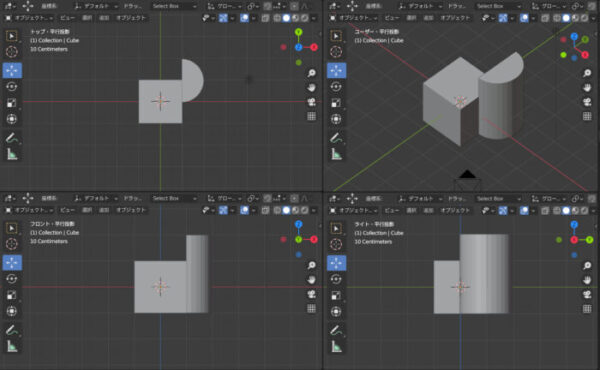
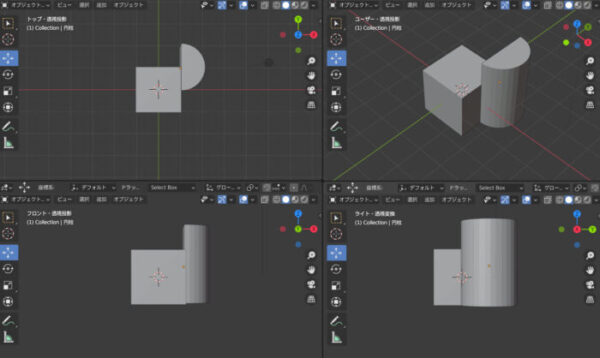
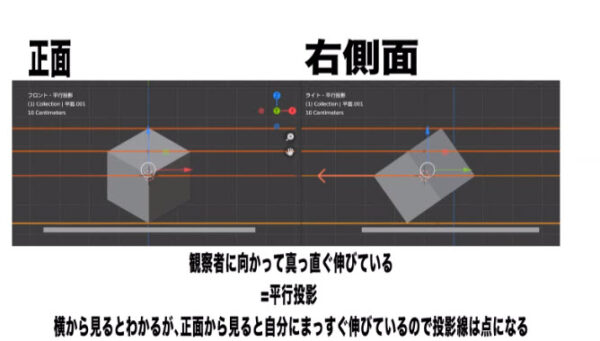
blenderでは正面がフロント、水平面がトップ、右側面図がライトと表示されています。Front view,Top view,Right viewの3つですね。
透視投影だと円柱の丸みが右側面でもはっきりわかりますね。平行投影だとほぼ直線です。丸みは水平面で確認しないとわかりません。
仮に立方体の三面図を作成したらこうなりますよね。正面、水平面、右側面、どれも同じです。
円柱のケースです。円柱の丸みがFやRでないじゃないか!まるで直線だ!と思うかもしれませんが、設計者の方はTで丸みがあることを脳内で補完して考えています。右上は平行投影ですが、立体感がありますよね。このような見方を平行投影では軸測投影といいます。平行投影には正投影と軸測投影がありますが、三面図の正投影のほうがよく使われるようです。立体的な軸測投影は便利そうですが、実際に設計する際にスケールがわかりにくいので不便だそうです。顧客の人にこのようなものができますよ、と提示したり商品説明で使う際には軸測投影が便利になるのかもしれません。
機械製図において平行投影は大事ですが、イラスト作成において平行投影が大事かどうか、正直わかりません。よく三面図でつくった人間は不自然だといわれる理由と関係しているのだと思います。自然な見え方は透視投影のほうにあるからです。ただ正確なものづくりという点では平行投影が大事だというのもわかります。
blenderで人間を作る場合は平行投影と透視投影を頻繁に行き来して、不自然にならないように調整したりしますよね。バランスが重要だと思います。平行投影のみの表示で人間を造形しようとすると、失敗してしまうかもしれません。あれ平行投影で完璧に作ることができれば透視投影に表示を変えれば済むのでは?という考えが頭をよぎりますが、人体を平行投影で完璧に作るというのがおそろしく難しいんでしょうね(?)。
軸測投影
軸測投影(じくそくとうえい,Axonometric projection/auxiliary):投影面に対して対象物を斜めに配置して投影図を描く方法。投影面は平行で、投影面に対して垂直であるので、垂直投影の一つである。対象物を投影面に対して斜めにおくことで、投射画像に立体感が出る。正投影のほうが対象物のスケールを確認しやすいので利点があるが、立体感を表現するために軸測投影はうまれた。軸測投影ではスケールの忠実性が犠牲になるという欠点がある。
軸測投影は等軸測投影、3軸測投影、2軸測投影と3つに分かれている。立方体の基準軸となる3辺で形を議論できるという意味で軸測という。3辺が等しい投影方法を等軸測投影、3辺がすべて異なる投影方法を3軸測投影、2辺が異なる投影方法を2軸測投影という。
何を言っているかわからない。そりゃそうですわからないです私も。わからないことを認めるというのは立派な前進です。
ということで、”どこが”わからないかを整理します。
等軸測投影(アイソメ)とは
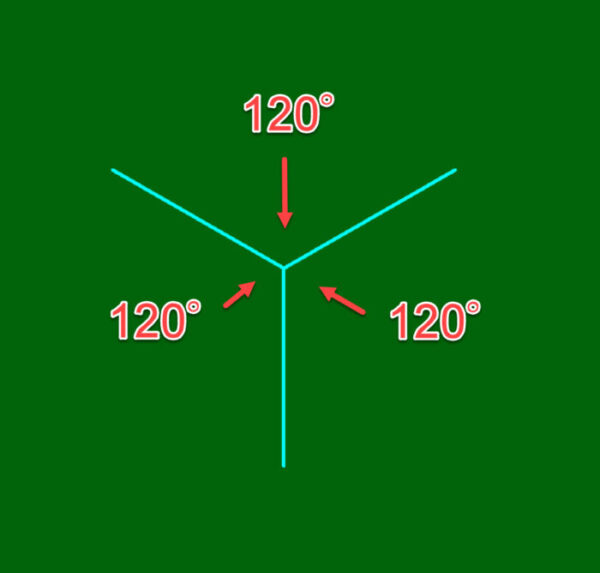
等軸測投影(とうじくそくとうえい,Isometric projection):3辺の長さがすべて等しくなる投影法を等軸測投影という。3辺がなす角度はすべて120度になる。等軸測投影は軸測投影の特別なケース。等軸測投影では対象物を斜めに配置するので、投影面に描かれる対象物の寸法は縮小される(√3/2≒0.81倍)。
縮小しないで実際の寸法で各方法を等測図またはアイソメ図という。アイソメ図は機械製図で立体を提示する方法として用いられる。
まず投影面に対して対象物を斜めに配置するとは?
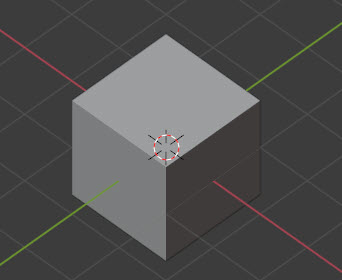
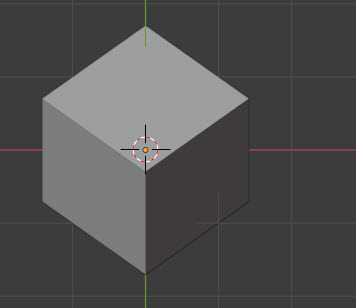
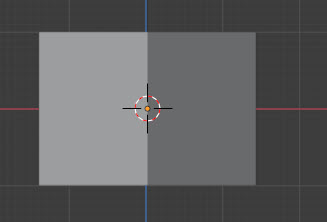
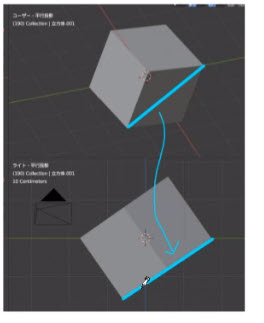
まずこれは対象物を斜めから見ている状態です。
これは対象物を斜めに動かして正面から見ている状態です。
形は同じですよね。しかし後ろのグリッドをみれば違いがわかります。斜めから見ていると、グリッドも斜めになっています。
対象物を斜めに動かしてから正面で見ている方は、グリッドがまっすぐ(垂直と平行)になっています。
だからなんだ?と言われたら閉口します。ただその違いを見つけました。
正投影から等軸測投影に変えてみる
これは正投影の三面図です。
等軸測投影の場合は、線が0.81倍に縮小されるそうです。
正投影のときの一辺の長さを100として、81の線を引いてみます。
等軸測投影の場合は3辺が同じ長さで、角度が120°ごとになります。360を3で割ると120ですよね。それぞれ120°になるように、81の長さを設定します。
さらにここから平行な線を同じ長さの81だけ伸ばしていきます。
あとは垂直線をまた81伸ばせば完成ですね。
おそらく破線で表示したりするのでしょうが、今回はパスします。
たしかに実寸より縮小されるとはいえ、全部の長さが同じなのでわかりやすいですね。描きやすいともいえます。
対角に位置する頂点が投影方向に一致している?
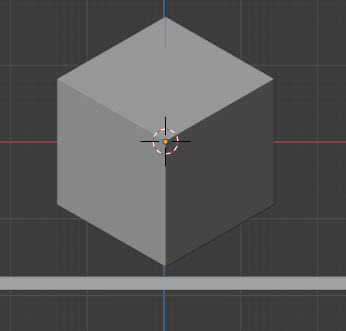
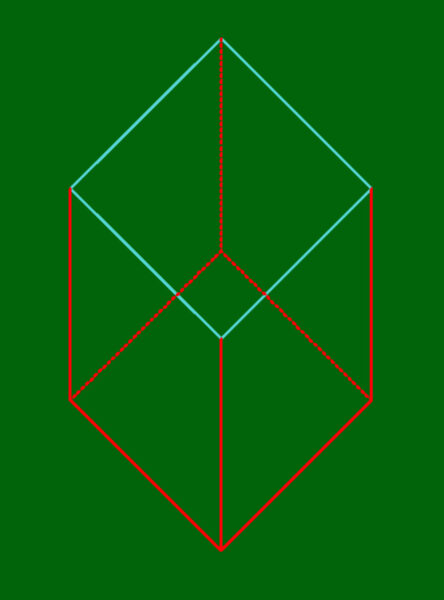
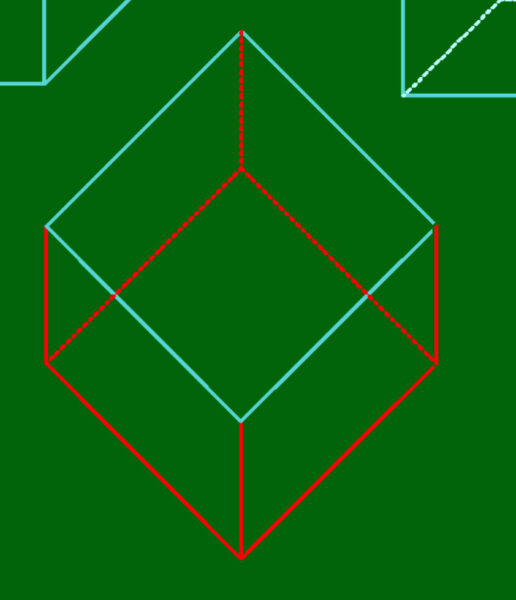
よくわかな。とりあえずblenderで斜めに配置を変えた状態の三面図を陰影ありで見てみます。
正直配置方法もよくわからないんですよね。
たしかに投影線がまっすぐのびてそうです。
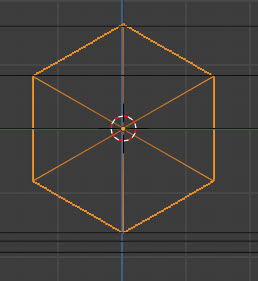
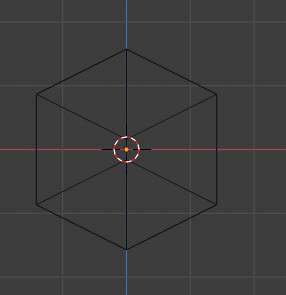
ワイヤーフレームで表示させるとより明確になるのですが、たしかに対角線の頂点が正面で一致しています。
まずZ軸に45°回転させます。
次にX軸に35°回転させます。これで等軸測投影のような見方ができます。しかしなぜ35°でできたのかわかりません。
30°だとあきらかに等軸測ではないんですよね。
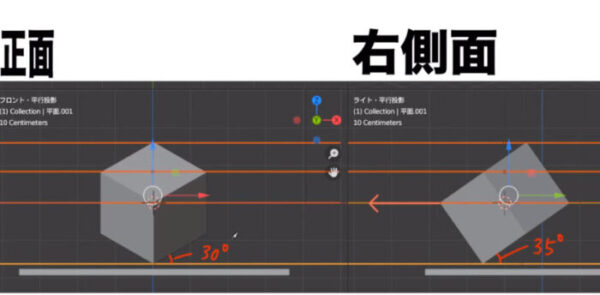
ディスプレイにアナログの分度器を乗せてみると、Xを35°に回転させた時、正面では30°、右側面では35°でした。
なるほどわからん。ですが等軸測投影では正面で30°になるらしいので、これは正しいんです。ここが30°ということは180-(30*2)=120なので、120°が3つできていますよね。
ちなみに35°の反対は55°でした。したがって、右側面は180-(35+55)=90°です。
詳しい理屈はわかりませんが、正面で30°にするためには、側面で35°にしないといけないのではないでしょうか。
立方体は絶対としてはたしかにひとつの面の角度は90度になります。しかし正面は30°なので、ひとつの角度が60°にみえていることになります。
したがって、右側面で180-(35+55)=90°になるのはなにか意味があるのではないでしょうか。
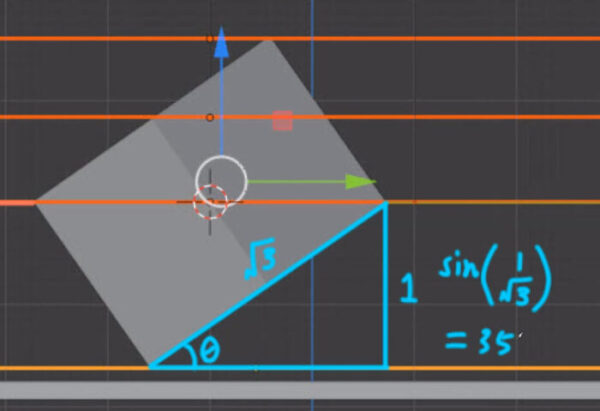
実際に10mmの長さはA’-O’になります。しかし図のように傾けるためのA-O(X)は10mmより縮まる事になります。1分は1度の60分の1(1分=1/60°)で、16分=16/60°=0.26666....°ですので、35°16’=35.2666....°となります。
X=10mm(A’-O’)×cos35.2667°(三角関数表で0.81647329...°)≒8.16mm(A-O)
つまり10mmだったA’-O’は傾けることによりA-Oは8.16mmという事になります。
このサイトに理由っぽいものが書いてあるようです。いや書いていませんでした。
等軸測投影の35° 出典
このサイトにそれっぽいものが文系の私には難解な方法で書いてあります。
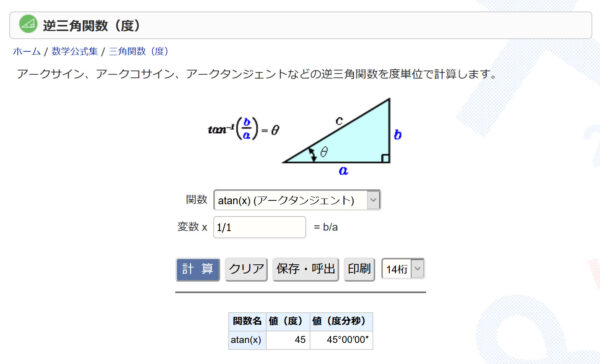
どうやらarcsin1/√3で出るようです。時代は便利になりました。計算ソフトがあります。
このようにでました。35°と出ているのであっているようですね。
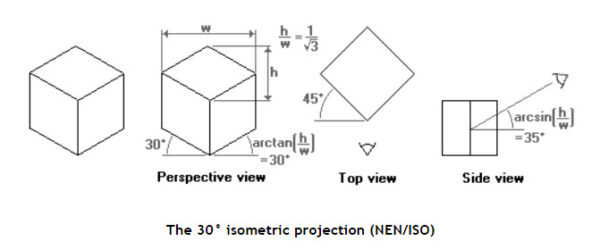
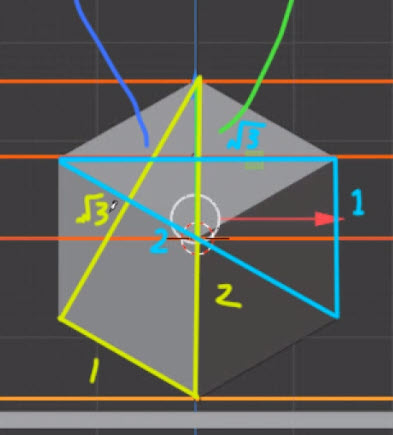
アークサイン、どこか遠い記憶に・・。というかWは√3なんですね。√2だと思っていました。あれ。一辺を1とした場合の対角線はルート2ですよね。あれそもそもWとHは同じ√2なのでは。
いや違う一辺の長さと同じになるので、1は1でいいんですよね。たしかにhは1です。なぜwが√3なのかが問題です。
たしかに図ってみると1.75近く、つまり√3なんですよね。
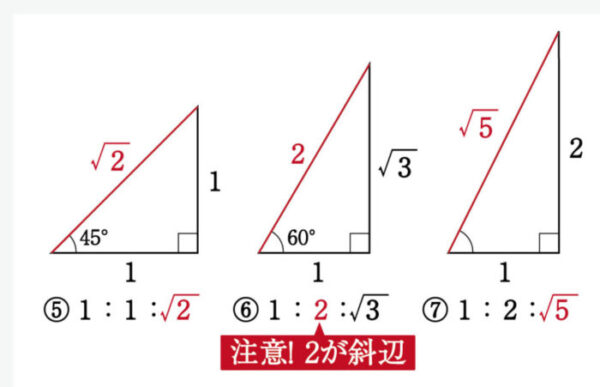
ああ、三平方の定理か・・
そんなのありましたね。そうかa√2は45℃のときでした。今回は60°なので、1:2:√3なんですね。こういうわかった!!ってときの感じたまらないですよね。
こういうことですね。
なぜ逆三角関数の計算式がそうなるのか、なぜ斜辺が√3になるのか、それはわかりません。ただθが35°なので三平方の定理は使えません。違う方向から√3を導き出すのだと思います。たとえば角から角への線の長さを√3だとすると、同じように右側面でも角から角の長さになるので√3だというふうな理解です。
最後にアニメーションを作ってみたので確認します。
斜投影(斜軸測投影)
斜投影(しゃとうえい,Oblique projection):投影線が投影面と斜めに交わる投影方法。一つの投影図で立体を表す投影。斜めの方角から平行光線をあてて投影する方法。正面図、または平面図の情報を保持しながら立体感を出す方法。正面図の情報を保持する方法をカバリエ投影、平面図の情報を保持する方法をミリタリ投影という。他にもキャビネット投影(カビネ投影)というものがある。
そうですよね、わからないですよね。こんな文字だけで言われたってわかるわけがない。
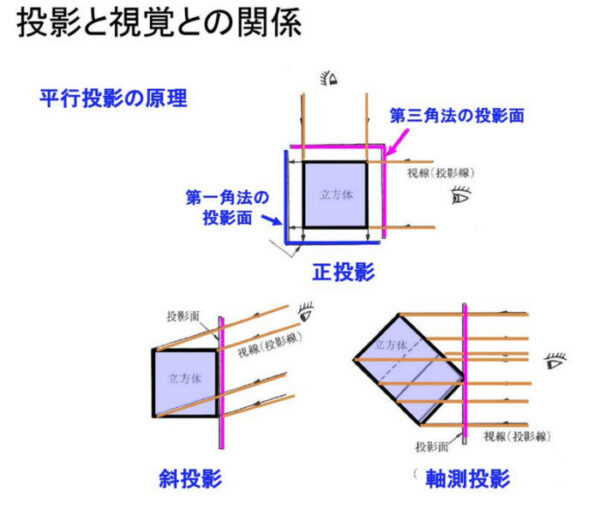
正投影と斜投影と軸測投影 出典
正投影と斜投影、軸測投影の素晴らしい比較図があったので使わせていただきます。なるほど軸測投影のように立方体は動かさずに、人間側の視線を変えるんですね。
ほー、わからん。なるほどまったくわからん。どう便利なんだろう。どこで使うんだろう。
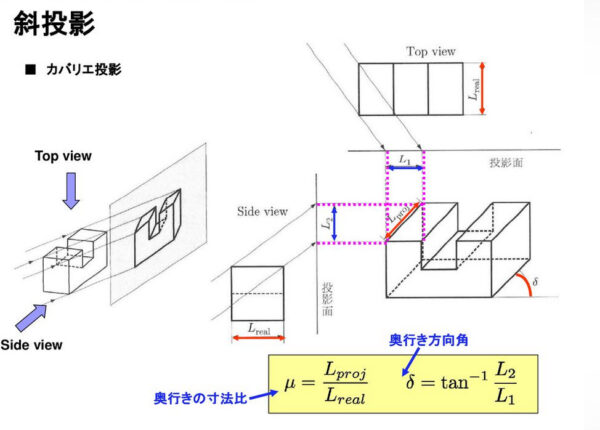
カバリエ投影
カバリエ投影(Cavalier Projection):正面図の情報を保持しながら立体感を出す方法をカバリエ投影という。平行投影に属する斜投影の一種。
こんなカバみたいなかわいい名前をしているが、意外と数学っぽい話になりそうなんだ。「例題で学ぶ図学 第三角法による図法幾何学」で使われている図説とスライドの図説がほぼ同じだが、有名な図説なのだろうか。
当然というかやはり、サインコサインタンジェントが出てくる。文系にはδの読み方すらわからない。調べてみるとデルタと読むらしいです。あーそういえば習った気がします。ちなみにμはミューと読みます。
カバリエ投影では正面図の情報をそのまま使います。ということは、考えなければ行けないのは水平面と右側面なわけです。つまりTとR(S)です。
そこで、どのくらいの奥行きにすればいいのか?という計算をしなければいけないらしいです。
おそらく上の図はμ=1/1(つまり1)で、δ=45°です。これはアナログの定規ですべて等しいことを確認しました。もちろん角度も。三角関数の計算を文系が必ずしも抑える必要はなく、計算ソフトを使ってしまいましょう。検索するとでます。
どうやら毎回逆三角関数を行う必要はないみたいです。作図のときにはμやδの値が与えられるそうです。参考書には30°、45°、60°の例が挙げられていました。
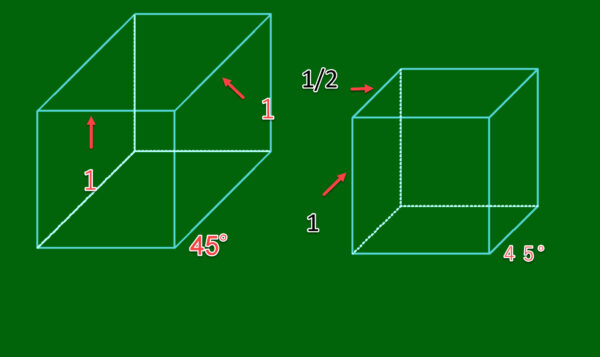
δ=45°でμ=1/2の場合をキャビネット投影(カビネ投影)というらしいです。カバリエ投影は奥行きが不自然になりがちなので、奥行きを半分にしたというわけですね。
CADで立方体をδ=45°、μ=1で書いてみました。μを1/2にするだけでキャビネット投影にできるんですね。キャビネット投影のほうが自然な立方体に見えます。
絵に使えるかどうかはわかりません。純粋に設計図として使用するなら正投影のほうがいいかもしれませんが、説明書で立体的に説明する時にキャビネット投影は有用かもしれません。
立体的に説明するなら透視投影でもいいじゃないか!という場合もあるとは思いますが、奥に行けばいくほど線の長さが変わってしまうと問題が生じる場合があります。
たとえば木材Aが長さ20センチが2個あるとします。しかし同じ20センチなのに奥にある木材が短く見えてしまうとどうなるでしょう。ある消費者は、木材Aより短い木材Bがない!と困惑するかもしれません。そんなばかな!と思うかもしれませんが、説明書では同じ長さのほうがわかりやすかったりするものなんでしょう。逐一これは木材Aですよ!と示すのも一つの手かもしれませんね。
blenderでも同じ長さなの透視投影で見ていると錯覚が起きてしまうのです。ほんらいなら自然な見え方なのですが、あれ、20センチより短いぞ?もっと長くしちゃおうとサイズを変更した結果狂ってしまうことがあります。したがって、長さを揃えたいときは平行投影モードにして揃えてあげる、というのも一つの手なのです。
そういった意味では透視投影以外に平行投影を使う意味はあるといえます。ガバリエ投影もキャビネット投影も平行投影の一種です。
ミリタリ投影
カバリエ投影(Military Projection):平面図の情報を保持しながら立体感を出す方法をカバリエ投影という。平行投影に属する斜投影の一種。
これは結局ガバリエ投影とほぼ同じですね。
練習問題としてδ=45、μ=1の立方体を描けというものがありました。
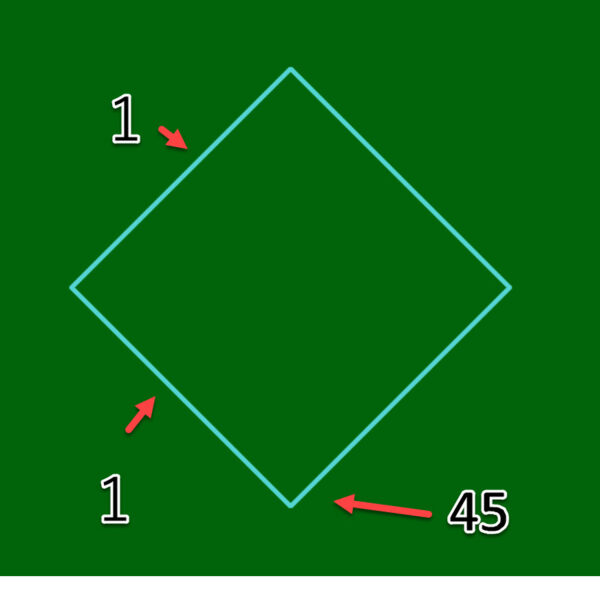
平面図とは、つまり上から見た図です。たとえばいっぺんの長さが1センチの立方体を想定します。そうすると、上から見て、かつ角度が45°になっているとこうなります。
μ=1なので、縦に伸びる長さもそのまま1になります。あとはつなげていくだけです。もし一辺が45センチなら、45センチ縦に伸ばせばいいだけです。μ=0.5なら、縦に22.5センチ伸ばすことになりますね。
もしμ=1/2ならこうなるのではないでしょうか。あまり自然には見えません。1/2にして自然になるのはキャビネット投影だけなのかもしれませんね。
参考文献リスト
1:「例題で学ぶ図学 第三角法による図法幾何学」,伊能教夫,小関道彦,森北出版株式会社
この本は意外ととっつきやすかったのでぜひ手にしてみてください。
2:「わかりやすい図学と製図」,住野和男,Ohmsha
難しいですが、より専門的で多くの知識が得られそうです。中級者向けだと思います。球体の描き方など、絵に通ずる内容もあります。
3:「図面の描き方がやさしくわかる本」,西村仁,日本能率協会マネジメントセンター
図形の書き方といういより、製図のルールが多い印象でした。
3:第三角法 MAU
4:https://slidesplayer.net/slide/11375695/(鄭聖熹さんという教員の方のスライドのようです。この人はスライドがわかりやすい。)
コメント
この記事へのトラックバックはありません。







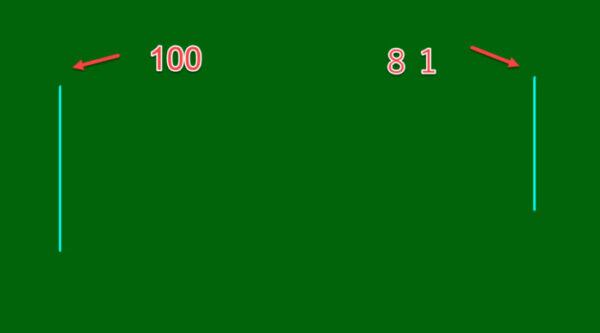














この記事へのコメントはありません。