円をきれいに描く方法あるのか

ただ練習すればいい、というのは正論であり暴論だと思います。絵は確かにデッサンや模写を繰り返して行うことで確実に上手くなっていくものだと思います。ただ私は絵を描くこと自体より仕組みというか理論というかそういうものが好きなので今回精神論的なものはひとまず棚に上げておきます。

いずれにしろデッサンの繰り返しで体がある種のコツを身に着けていくのだと思います。理論として言語化できなくても、そうしたなにかを上手い人は掴んでいるはずです。「慣れているから、体が勝手に覚えているから」と感覚としてはそういうものですが、突き詰めればなにかコツというかメルクマールがあるはずなのです。ギターの弾き方も同じようなものがあると思います。

また意識を持ってデッサンすることで、何も考えずにただデッサンするのとでは効率化という意味でも違ってくると思います。私が絵を描く人のためになにか手助けできるのはこういった側面だと思っています。

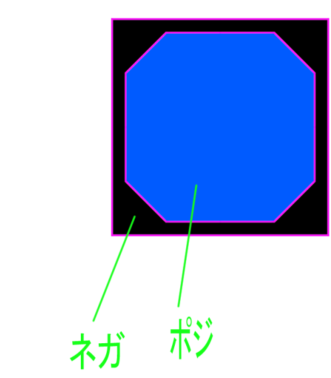
今回の目的は「正方形における円のネガスペースを見つけること」です。ネガとはポジではない部分を指し、ポジとは今回のケースでは円を指します。つまり正方形から円を引いたスペースがネガになるわけです。ネガには円が描写されないという意識を身に着けることで、すこしでも円がきれいになるのではないかという仮説です。

https://drawpj.com/draw-perfect-circles-freehand/

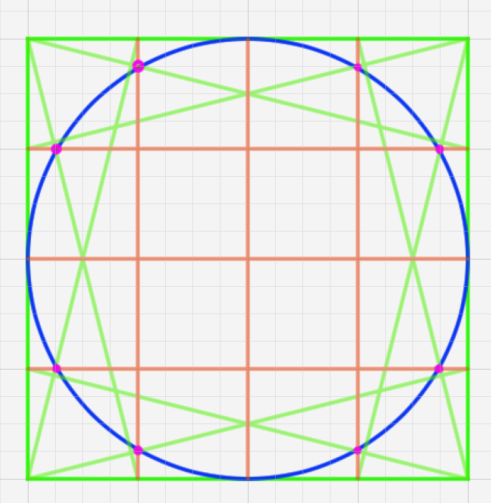
たとえばこのサイトのように、メルクマールとなる点を見出してきれいに円を描くというものがあります。このメルクマールを心の目で見出している人は、この点がなくてもきれいに円を描けているのだと思います。

さてこのメルクマールは正確にはいくつでしょうか。

補助線を使って円を考える

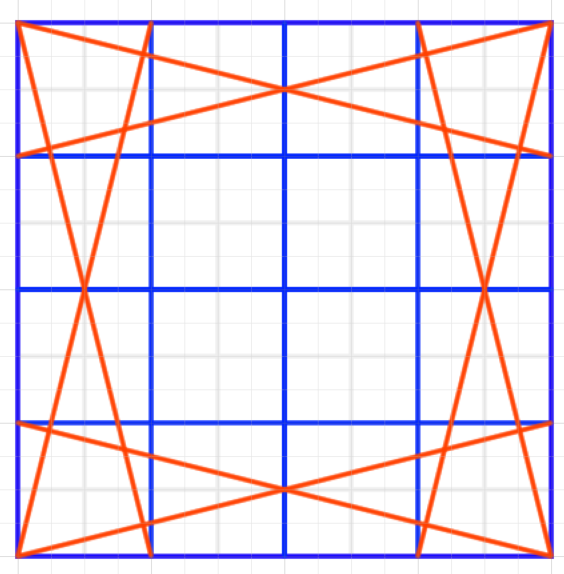
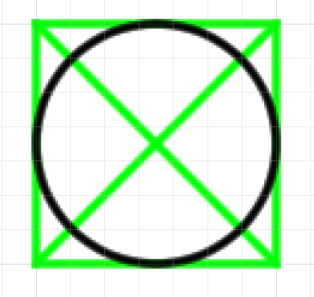
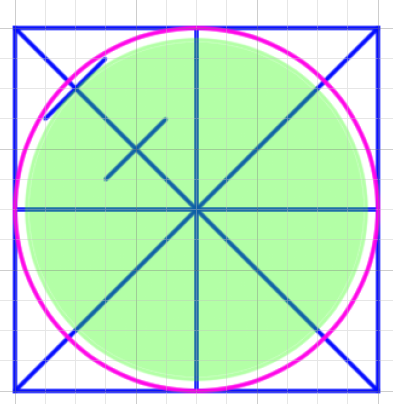
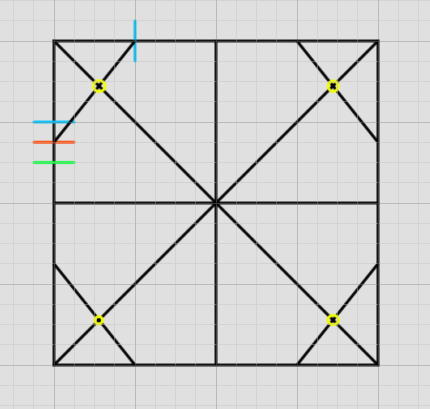
８分割をベースに考えればこのような補助線が出来ます。

これがベースの８分割です。

全部引く必要はありません。単純に呼ん分割の対角線を利用すれば８分割を見つけることができるからです。

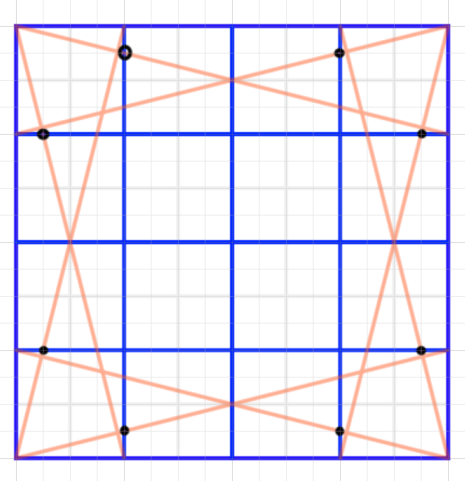
重要なのは四分割線と対角線の接点です。これを見つけていきます。左右合わせて8個あります。

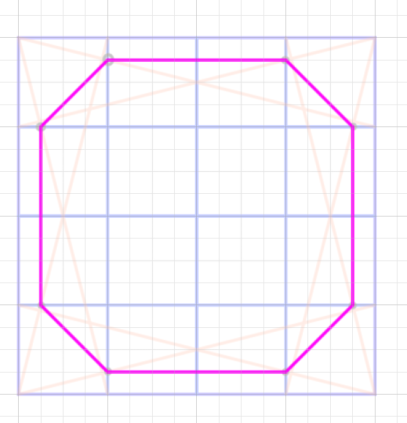
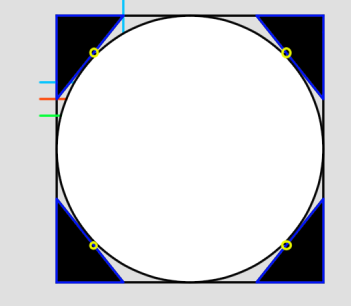
結び合わせると8角形になりますね。ポイントはポジに対するネガが1/16というところでしょうか。8分割をさらに分割したスペースです。

ネガとはポジではない部分のスペースです。ここでいうポジは８角形です。

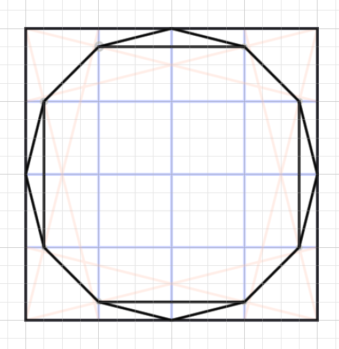
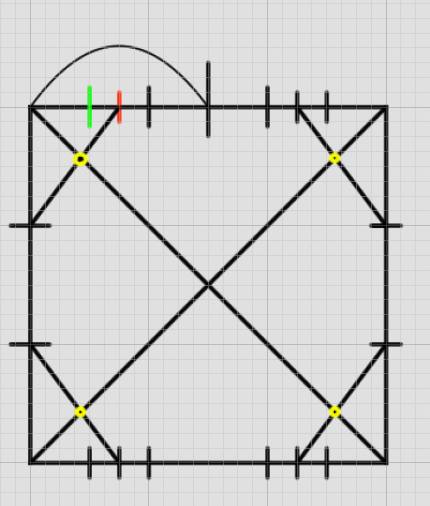
さらに加えるとしたら、十字に相当する４つの点ですね。結ぶとこうなります。

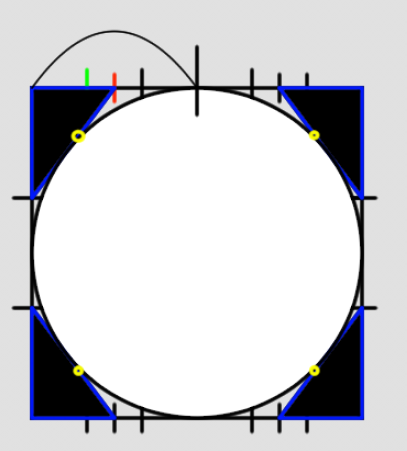
円に近づきましたが、本来の円の丸みには届いていません。

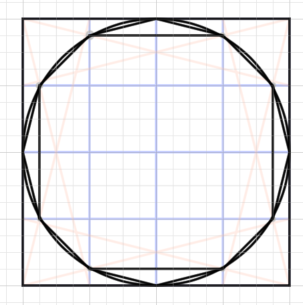
さて残りの点は難しそうです。偶数の分割ではもともと届かないのかもしれません。奇数にしてみると、ちょうど見つかりました。ちなみに27*27です。

違う分割でも探してみましたが７*7もわりと近いですね。いわゆる最小公倍数？ってやつですかね。

27*27の倍も割合で言えばネガは1/7ですからね。

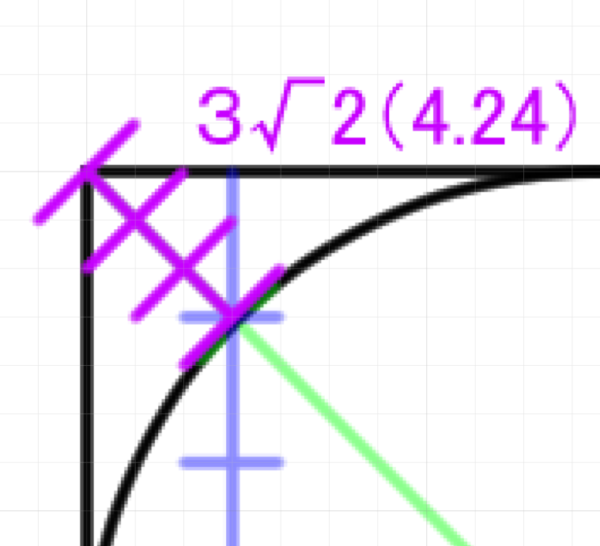
さてルートにするとどのくらいになるのか。3√２くらいですね。√２が1.4くらいなので、4.2ですね。ちなみに対角線は辺が１の場合、√２になります。

さて最小公倍数にすれば√２になりますね。つまり1.4くらいです。

つまり角を利用するなら９分割が望ましいかもしれません。

なんとか８分割ベース、あるいは４分割ベースで解決する方法はないものか。たとえば８分割ベースの場合は対角線の中心から角までの長さが４√２になります。

 

1.4(1/5.5)=0.25という結果が出ました。

つまりネガから数えて√2+0.25ということになります。1.65くらいですねざっくり。これは使えそうもないかもしれない。でもある種の目安にはなる。しかし奇数と偶数の分割を同時に存在させようとすると複雑になってしまう。

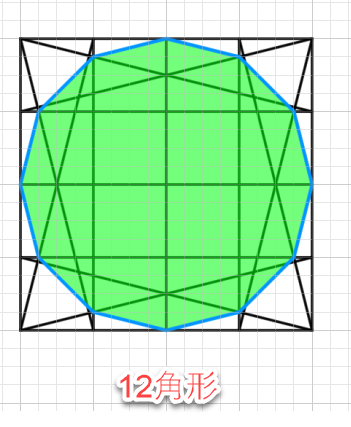
やはり対角線以外の、つまりこの12角形を基本形として、あとは丸みを自分で補完すればいいのではないかということです。作業のひとつとして、√2+1/4√2という知識はあってもいいかもしれません。なくても困らないでしょう。

いちいち対角線を引くのはめんどう？

たしかにそうだ。

そもそもどういう意図で円をきれいに描くかによると思います。

今回は顔で使いたいので、ルーミスの6分割を想定して円のポイントを探していきます。

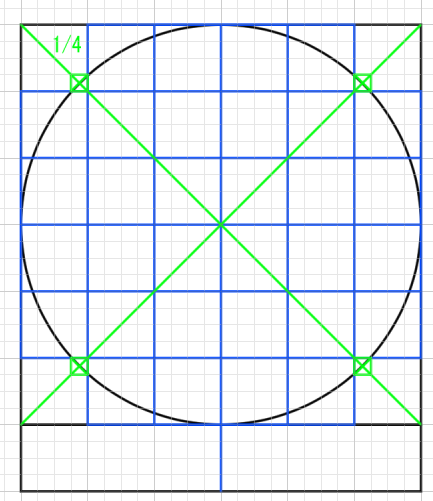
わかりやすい点が1/4にありました。6分割の中に4分割を織り交ぜるのは複雑なようですが、意外とそこまでではないです。

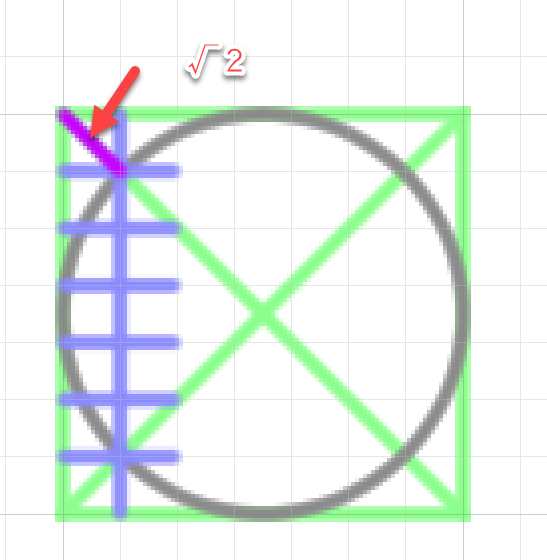
√２をさらに1/4したところと考えてもいいですね。0.35くらいです。

正確には1/4の線上にあるわけではなく。1/8の線上にあります。1/8はわかりにくいので、1/4の正方形を作って対角線を作り、その中心という形にしたほうがわかりやすいと思います。

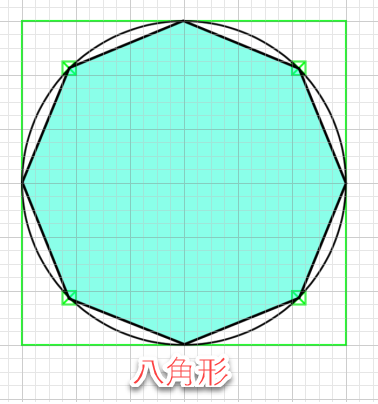
めやすはこの八角形ですね。

フリーハンドでは正方形さえかければましな円が描けるのではないか

そういわれればそういう気もします。正方形のかわりにきれいな十字でもいいかもしれません。

結局どこまで正確性にこだわるかということになりますね。デジタルなら図形ツールできれいな円をつくれてしまいます。結局はフリーハンドでどうするかというアナログの問題になってしまうかもしれません。それもコンパスを使えばいいのでは？というそもそも論がでてきそうです。

妥協案

まず8分割はめんどうです。わかりにくい。いちいち分割してから円を描くのはたしかに面倒だ。製図や建築ならその必要があるかもしれない。でも落書きやデッサンでそのようなことはしたくない気持ちもわかる。かといってデジタル描かない人もいるから、デジタル定規を使えともいえない。

さらにアナログ定規も使いたくないという人もいそうだ。

そこでまずは3分割のうちの1分割を目安に妥協してしまうのはどうだろうか、と考えた。だがそれは失敗だと気づいた。円が小さくなってしまうし、十字の点がうまく活用できない可能性がある。

なんとか√2＋0.25に近づけたい。そしてこの2.5に関連する線を見つけることにした。これもあまり使えそうもない。1を5:7にわけるという作業がそもそも面倒なのだ。

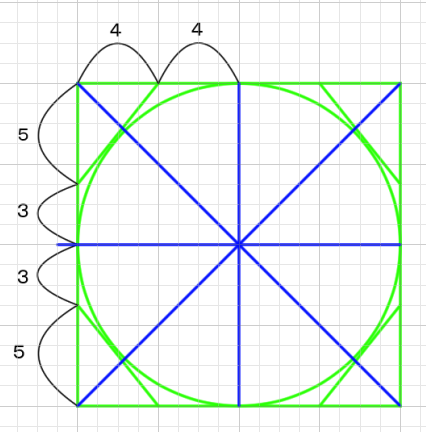
もっと妥協できる道はないのだろうか。こんなのはどうだろうか。このくらいなら妥協できる気もする。８分割ベースは十字を利用しやすいので、そこまで複雑ではない。さらに増やせば容易に１６分割ができる。

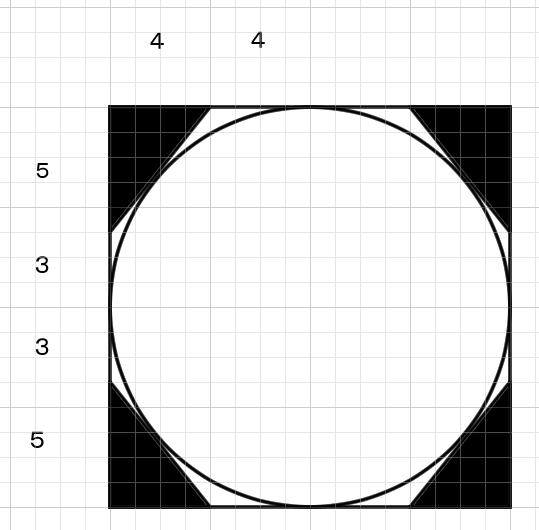
イメージとしてはこのようなネガスペースを定義することで、ポジである円が描きやすくなる感じだ。

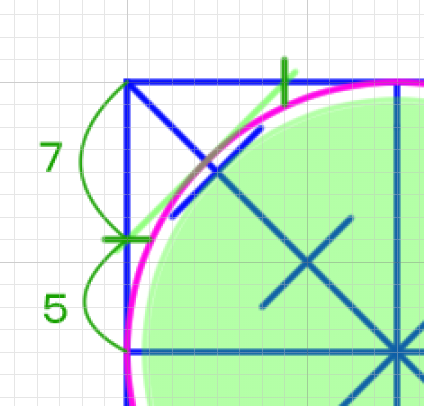
問題は5:3をうまく定義できるかという点にある。

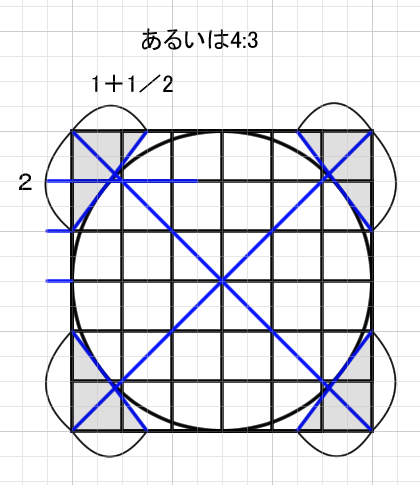
あるいは6分割ベースで一部に12分割を取り入れるという方法がある。6*6では2:1+1/2、12*12では4:3になる。

ルーミスの顔ではベースが６*6なので役立つケースがあるのかもしれない。ただきれいな円を簡略的に描きたいなら2*2ベースを基準にして考え、8*8を部分的に取り入れて5：３に分けて補助線をひけばいい。

十字から構成する

アナログフリーハンドを想定した場合、まずは自力で均一な十字を構成する。これができなければ始まらない。こればかりは訓練するか、定規を使うかしないとだめだ。線の等分感覚というのはある種の集中力を必要とするので、そういうところ絵の上手さが立ち現れてくるのかもしれない。

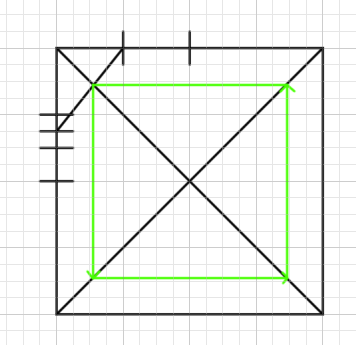
つぎは正方形を十字を使って構成します。

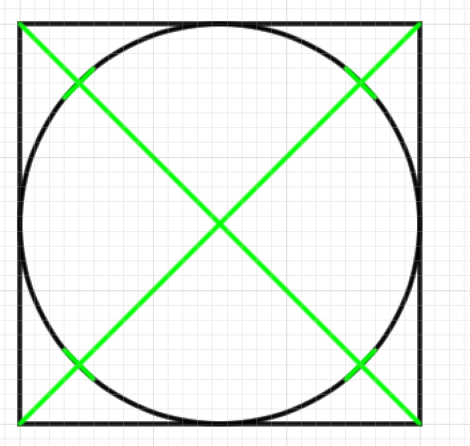
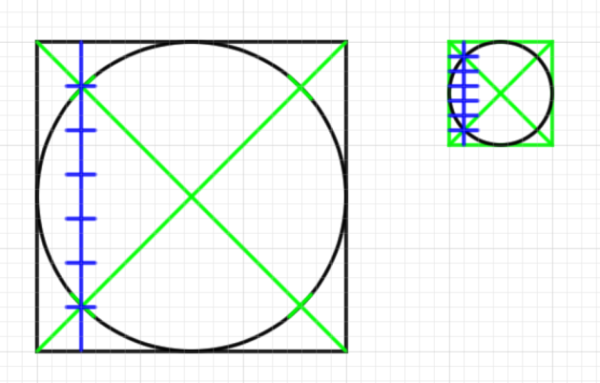
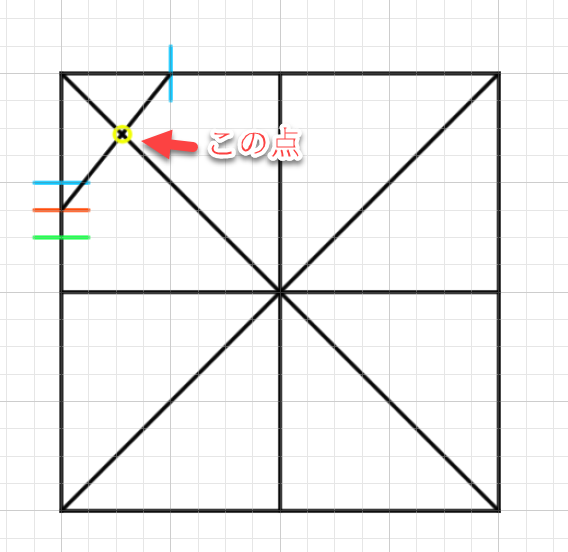
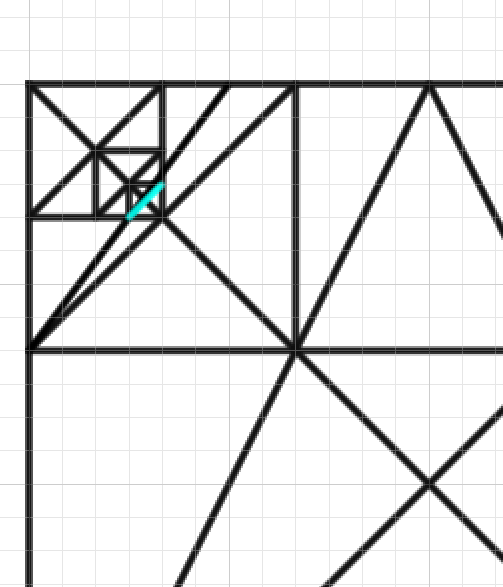
次に「対角線の点」をみつけます。今回は８分割ベースを使います。

今回はすべて８分割にするのではなく、部分的に分割します。まずはこれで左上の正方形がさらに分割されました。つまり左上だけ4*4ベースになります。

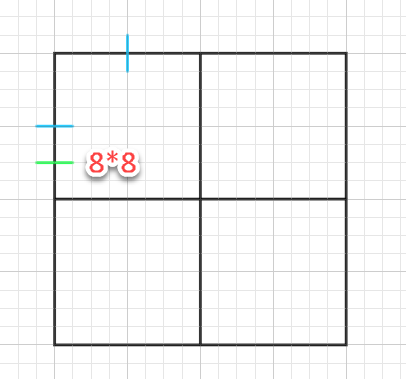
さらにまた左下の正方形を分割すれば、そこだけ8*8になります。

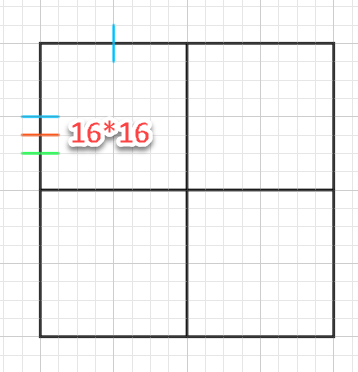
さらに分割すれば16*16です。

正確に分割したい場合で定規もない場合、かつ感覚的な等分に地震がない場合は対角線を使うといいかもしれません。

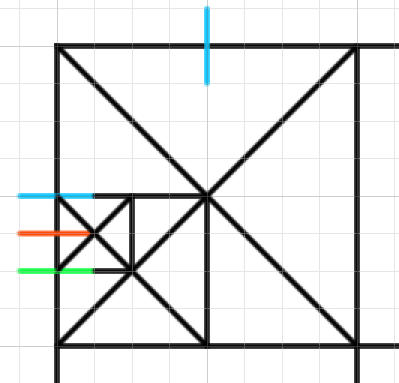
16にすることによって4分割したときの各正方形が8分割されることになります。つまり5：3にわけることができるようになります。部分的に分割することで作業を省略できています。

同じ作業をほかの角にも行います。

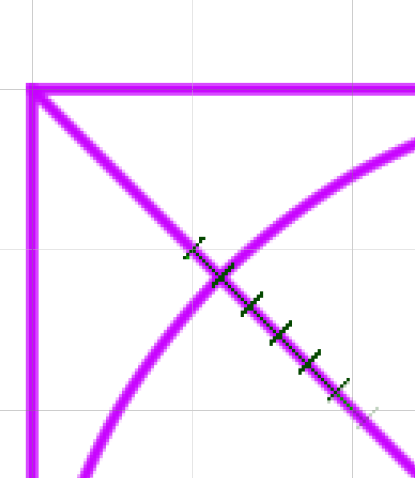
これでネガスペースが確保でき、円も描きやすくなるはずです。このような複雑な工程を得ないでも、単純に√2+1/4を目安にするといいかもしれません。抽象的な言い方をすれば、対角線の中心から角までの長さの1/3より少しだけ長い点です。

6分割ベースでも同じように分割していくだけです。割合はさきほどとは違います。

これでネガスペースができます。

これが役立つかどうかはわかりませんが、分析するのはとてもおもしろかったです。すべてのネガを特定してしまえばポジだけになり、より正確な円を構成することが出来ます。しかしそれでは作業が大変なので、特定のネガを見つけてポジを描きやすくするというのがポイントだと思います。少ないコストでどれくらいのパフォーマンスができるか、そういった問題だと思います。

 

ちなみにひとつの対角線上の点がみるかれば、ほかの点を見つけるのは容易です。ほかの対角線まで直線を伸ばしていくだけです。

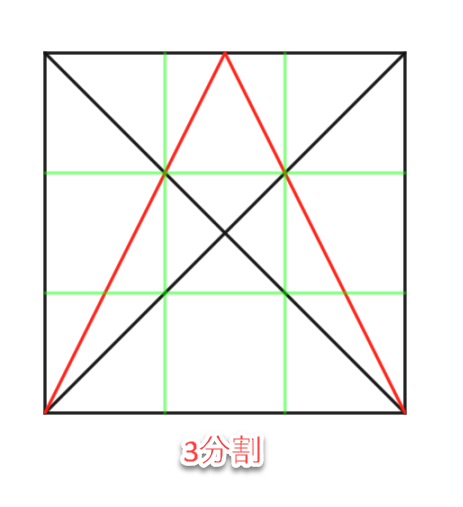
3分割を構成する場合

三分割の場合は斜線をうまく使いましょう。３分割と書いていますが、１辺を３に分割するという意味で、3*3という意味です。実際には９分割です。

正方形を分割する方法とは、やり方(2分割、3分割、5分割)

 

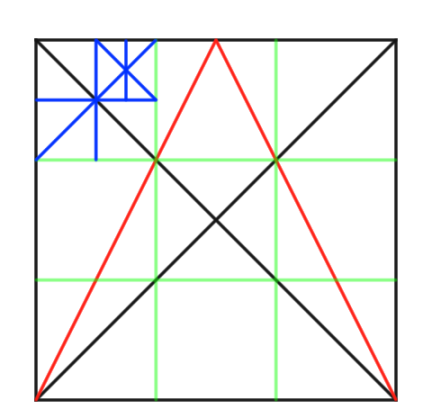
さらに対角線をつかえば正確に部分的な6分割や12分割を行うことが出来ます。

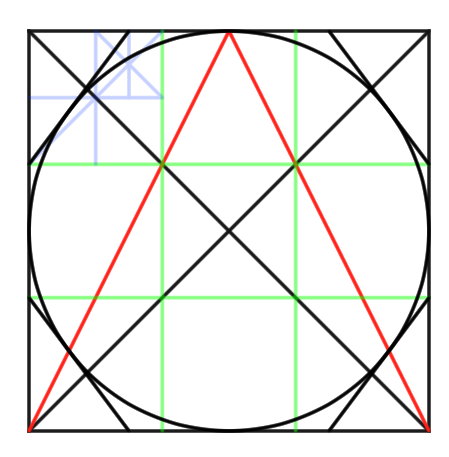
先程の円を適用させるとこうなります。

ちなみに対角線を利用した方法では、この方法もありますがやや複雑ですね。