【動画解説つき】一点､および二点透視図法で斜めに傾いた立方体を正確に描く方法

はじめに
- 動画での説明
一点透視図法で蓋が斜めに傾いた立方体を描く
【補論】二点透視図法において角度が変化した場合の画面と視心の遷移について
【補論】２点透視図法で段ボールを描く(COV2のケース)
【補論】２点透視図法で段ボールを描く(COV1のケース)
【補論】３次元ソフトと２次元ソフトの一致について
次回の予定
参考文献

はじめに

動画での説明

・この記事の「概要・要約」はyoutubeの動画の冒頭にありますのでぜひ参照してください｡

よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m

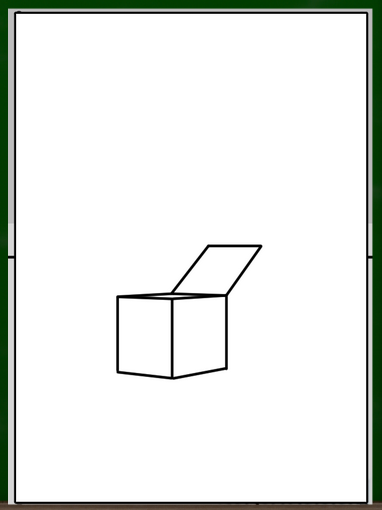
一点透視図法で蓋が斜めに傾いた立方体を描く

立方体は何度に､どのように傾いているのか情報を集める

なにごともまず､情報から集めなければいけない｡段ボール(立方体)は､どのように開いているのかという問いをまず設定する｡

A:傾いているように見えるが､実際には９０度でまっすぐ蓋が開いている｡
B:傾いているように見え､かつ､実際に９０度以外の角度で蓋が開いている｡

Aのケース:傾いているように見えるが､実際には９０度でまっすぐ蓋が開いている｡

まずは９０度で蓋が開いているケースである｡これは真横から見た平行投影の側面図である(パースがかかっていない)｡わかりやすいように､蓋に厚みをつけた｡

この段ボール(立方体)がさまざまなカメラの角度や立方体自体の回転によって｢斜めに見える｣場合がある｡

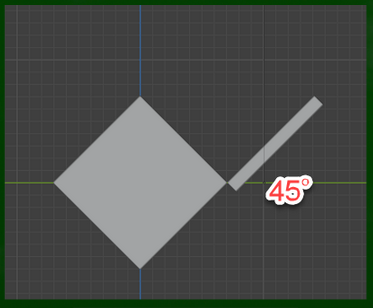
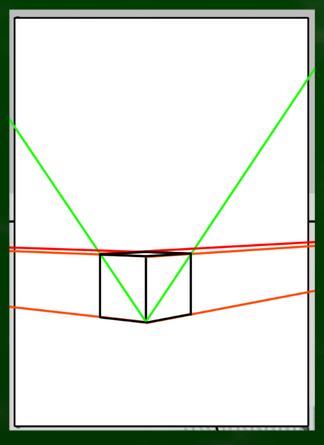
先程の段ボールを､４５度(x軸)傾かせてみる｡カメラではなく､段ボールのほうが物理的に傾いたケースである(段ボール自体は物理的に斜めになっていないが､傾いているというややこしい話)｡

カメラを動かして三点透視図法風にすると､蓋も斜めに傾いているように見える(段ボール自体が物理的に斜めになっておらず､かつ傾いておらず､斜めに見えるケース｡こちらがAとしては適切な具体例)｡純粋に｢収束によって斜めに見える｣ケースである｡

Bのケース:傾いているように見え､かつ､実際に９０度以外の角度で蓋が開いている

蓋(だけ)がそもそも傾いている(物理的に斜めになっている)ケースがこちら｡

同じく平行投影である｡

今回はこのBのケースを扱う｡

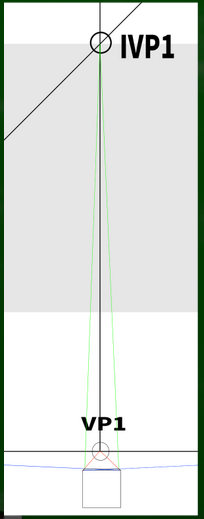
傾斜消失点を使って斜めの箱を描いていく

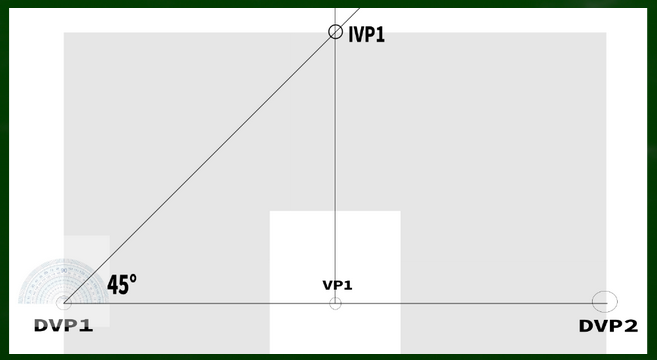
前回の記事では｢傾斜消失点｣を用いて階段を作った｡今回も､傾斜角度45度を基準に､一点透視図法でIVPの位置を設定してみる｡

【第十四回】パース基礎:｢追加消失点で階段を描く方法｣を解説

ただし､今回は階段を描く方法とは少し違う､幾何学的な手法を試す｡

今回は高さと幅､そして奥行きが100cmの段ボールを想定して作図してみる(見やすくするため大きくしたが､文字通りの意味での一般的な段ボールはもう少し小さいだろう)｡

※一点透視図法における立方体の作成方法は以前の記事(第三回)を参照

【第三回】パースの基礎を学ぶ:一点透視図法で立方体を作成する方法､対角線の消失点について

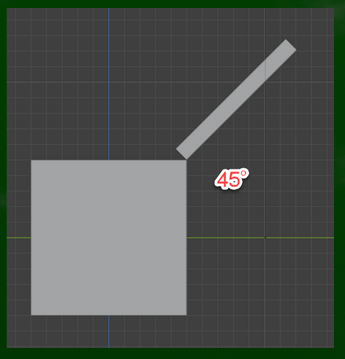
ここに､蓋をつける｡蓋はVP１へと伸びているわけではない｡言い方を変えれば､観察者に対して平行な線ではない｡

たとえばサイコロを考えてみてほしい｡どの辺も物理的には真っ直ぐであり､斜めではない｡一点透視図法や二点透視図法､三点透視図法ではその｢斜めではない線が収束することによって斜めに見える｣ことを我々は学んできた｡

しかし今回は｢斜めではない線｣ではなく､｢斜めである線｣を扱う｡言い方を変えれば､観察者の真っ直ぐな肩とは違う角度の線を扱うというわけである｡

｢斜めである線｣なのだから､｢斜めに見える｣のは当たり前であるように思える｡しかし､この｢斜めである線｣は一点や二点透視図法における消失点へは収束しない｡

ではどこに収束するのかというと､｢追加消失点｣へと収束するように見えるというわけである｡

どこにも(追加消失点にも)収束しないように見えるタイプの線を､前回は｢積み木ケース｣と呼んだ｡今回は｢段ボールケース｣である｡階段のケースも段ボールケースの一種であるといえる｡積み木ケースももしかしたら規則性があるのかもしれないが､描画においてはただ線を結ぶだけなので考慮しないことにする｡

先程の図で言えば､｢斜めではない線(90度)｣からなる立方体に､｢斜めである線(45度)｣からなる平面がくっついているということになる｡

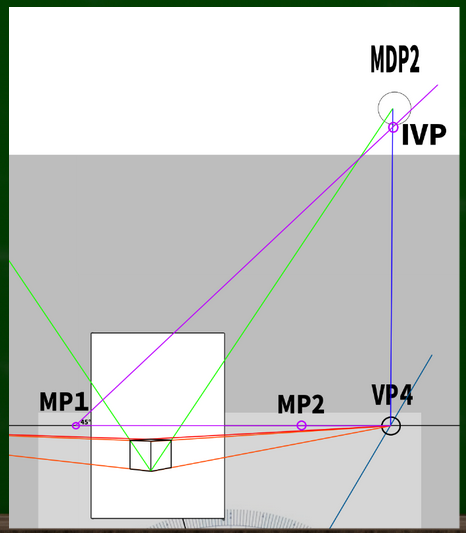
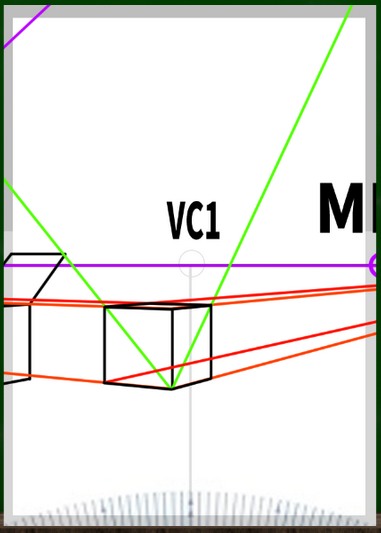
まず､IVP１へむかって線を伸ばしていく｡

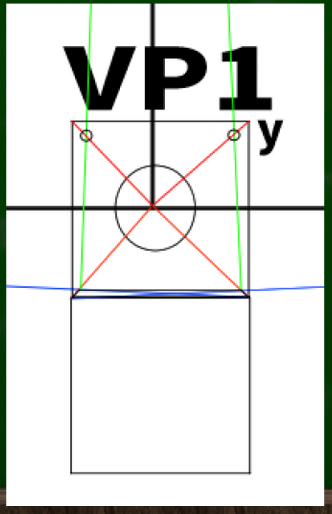
次に知りたいのは､蓋の高さである｡手前にもうひとつ正方形を作り､消失点へと伸ばしていくと､蓋の高さの指標点がわかる(?)｡

これで蓋が45度にかたむいた段ボールが完成する(?)｡

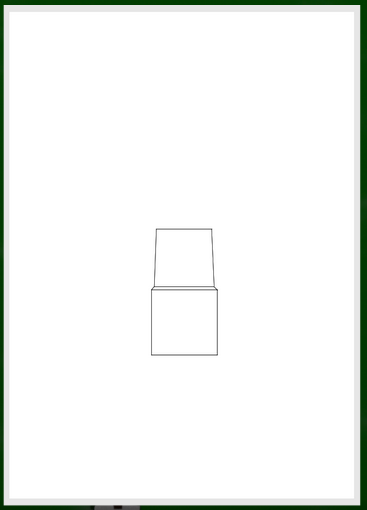
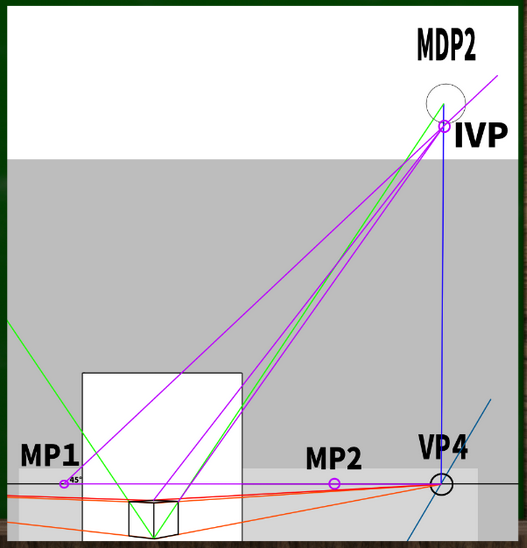
しかしblenderの画面と比べてみると､どこか蓋が大きすぎる気がする｡

発明家のエジソンが「失敗ではない､うまくいかない方法を1万通り見つけただけだ」と言っていたが､失敗に見えるものも貴重な財産となる｡

考えられる理由は､高さの基準となる手前の９０度の立方体がまず挙げられる｡つまり､手前も４５度の角度に変更し､そこからVP１へと線を伸ばすことで修正できるというわけだ｡

しかしそもそも４５度の角度の正方形ができないから困っているわけなのであり､根本的な解決にはならない｡

幾何学的･数学的な解決

やはり幾何学の問題となるのだろう｡９０度ではなく４５度になった場合､直線の高さはどのくらい低くなるのかという問題である｡

ただし､正面から見て４５度というわけではなく､側面からみて４５度であるという点がポイントである｡

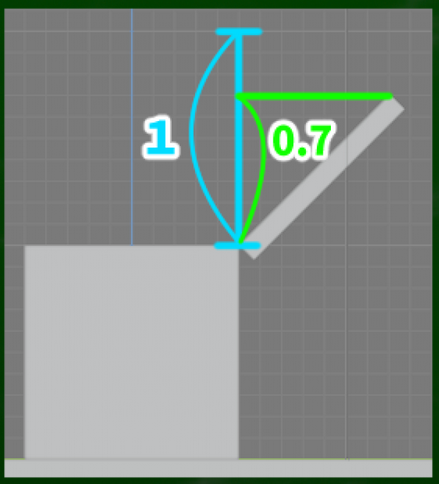
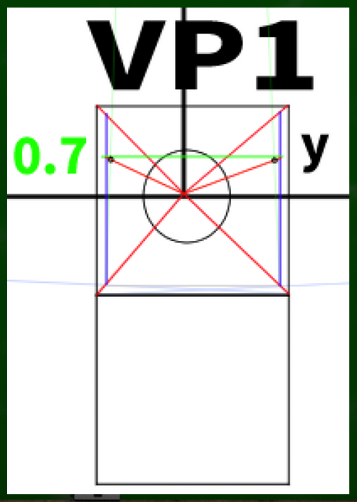
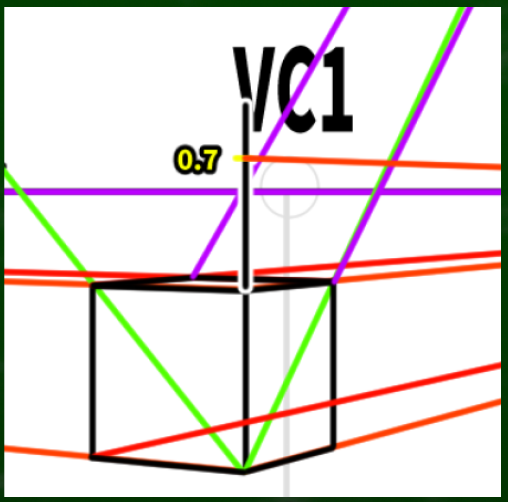
詳細は省くが､数学的には実測の長さ×sin(45°)となる｡ようするに､およそ0.707倍になるというわけである｡※理解できなくとも､Google電卓を使うなり､AIに聞くなりすればなんとかなる｡

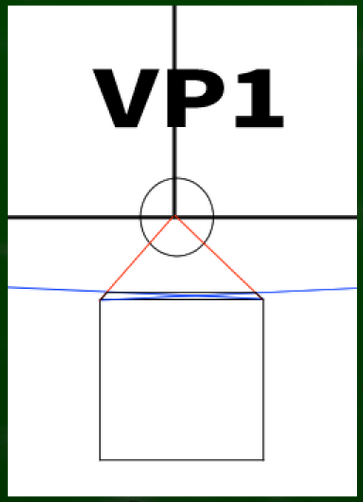
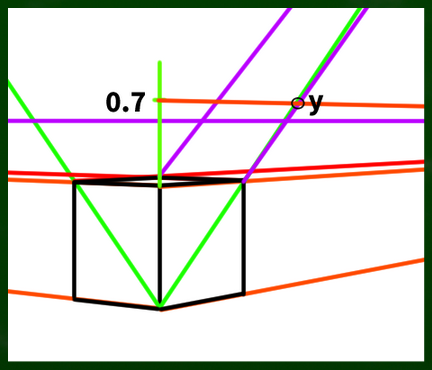
図で説明するとこのようなイメージとなる｡

およそ0.7の位置にチェックをつけ､そこから収束させていけば正しい奥行きの指標点が判明するはずである｡

一点透視図法なので､垂線を定規で測って0.7の位置を見つければいい｡10センチなら7センチ､5センチなら3.5センチの位置だ｡

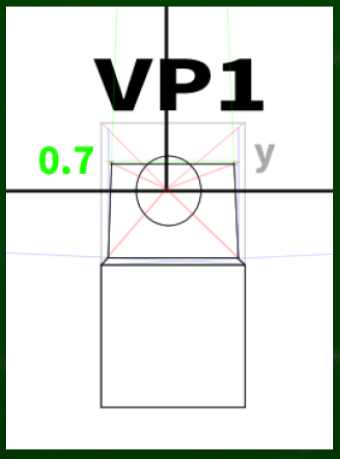
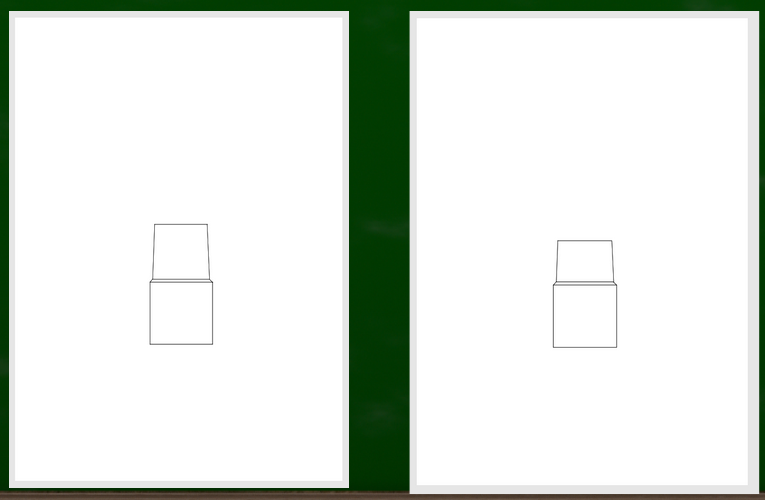
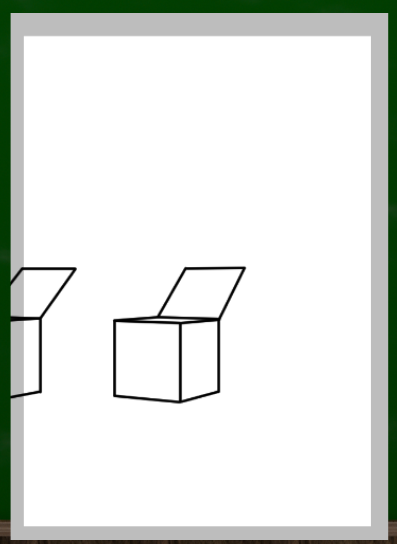
新しいyを基準に蓋を描くとこのようになる｡

修正したほう(右)がやはり自然に見える｡

【補論】二点透視図法において角度が変化した場合の画面と視心の遷移について

以前からよく理解していなかった基本事項がある｡たとえば二点透視図法のある状態から､視線を左にn度傾けた場合の視心(VC)と画面(PP)の変化はどのように把握できるのか｡非常に重要な要素だが､曖昧にしか私は理解できず､やり過ごしていた｡

※この項目はやや複雑で､かつ実験的な考察なので興味がない人は飛ばしてしまってもかまわない｡しかしここを曖昧に理解していると､曖昧なパースしか使えない気がする｡

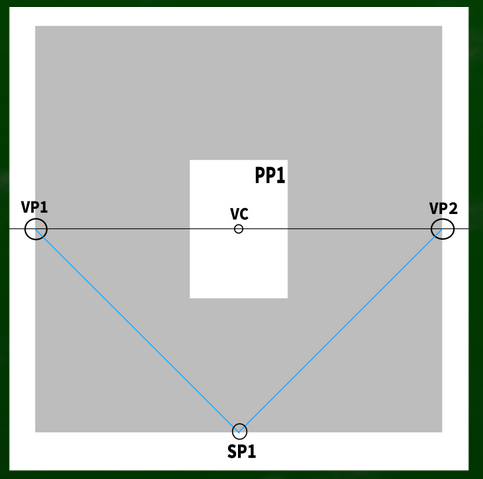
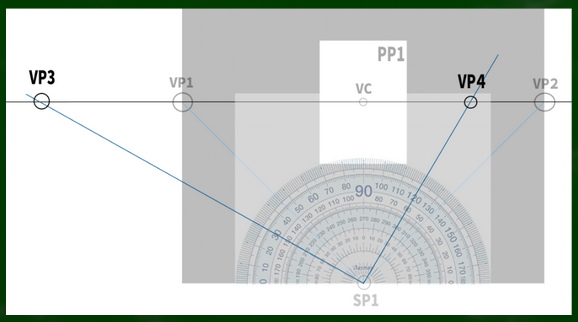
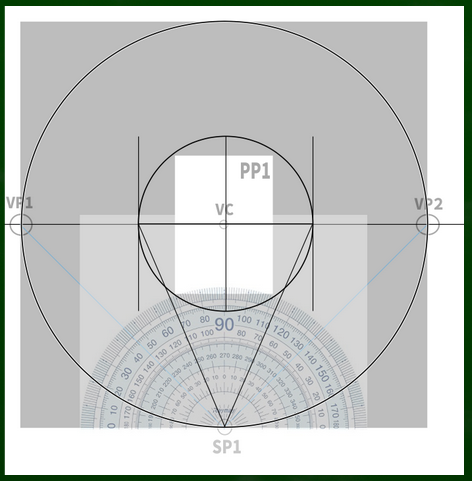
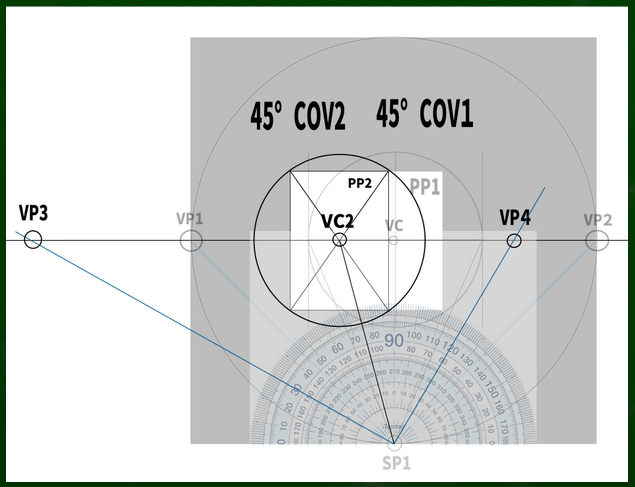
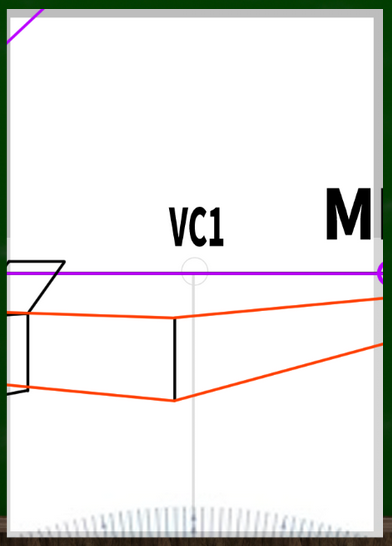
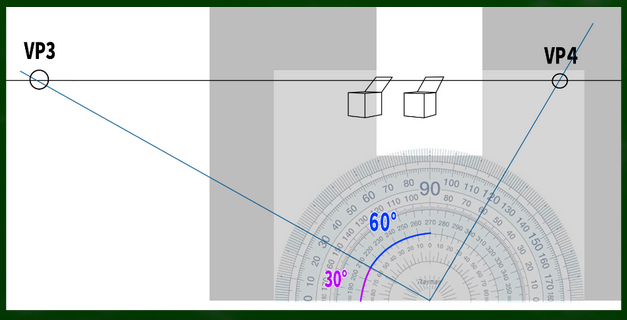
たとえば､左右に45度のケースではこのような画面構成となっており､画面(PP)が視円錐(COV)45度に収まるようになっている｡そして視心(VC)も画面の中心にある｡

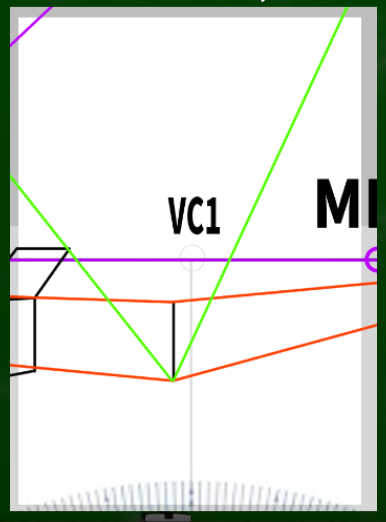
さて､ここから､左に60度､右に30度になるように変化させるとこのようになる｡つまり､15度左に頭を傾けたというわけである(45+15,45-15)｡頭を傾けただけなので､SPの位置自体は変わっていない｡

もし視線が15度傾いたなら､視心も15度傾いた位置にあるのではないだろうか｡

つまり､75度の方向に線を伸ばし､HL(水平線)と交わる点が新たなVCとなるのではないかという仮定である｡

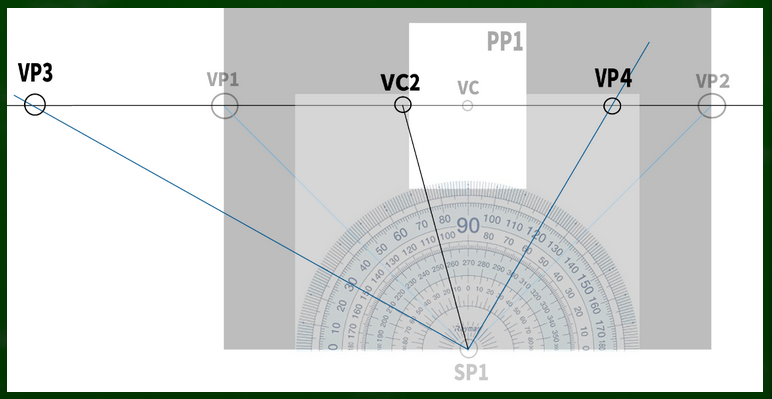
45:45の場合の視円錐はこのように構成されていた(画面をぴったり収めるケース)｡

もし視心が変化するならば､それに合わせて視円錐の位置も変化すると仮定する｡

それぞれの角度を調整すると､このようになる｡

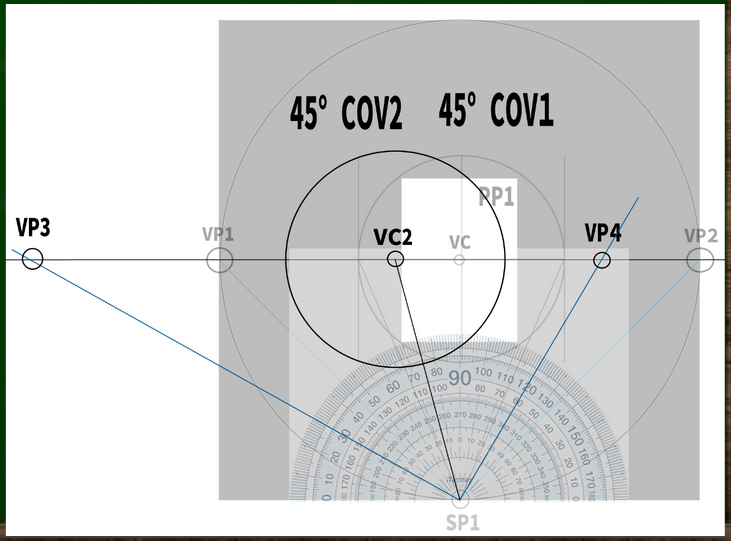
最初の45:45の画面のままでは視円錐45度におさまっていないため､画面を新たな視円錐に収まる位置まで調整してみる｡

もしblenderで表現するなら､このような変移となると仮定できる｡

しかしVC(視心)の位置がそこまで重要なのだろうか｡二点透視図法で立方体を作図する場合､VCを使う機会はあまりない｡消失点が同じ位置なのだから､立方体の作図に直接的には影響してこない｡

重要なのは｢どの辺りに画面を構成するかという初期設定｣であり､｢VCを基準にして視円錐が構成されるという前提｣である｡

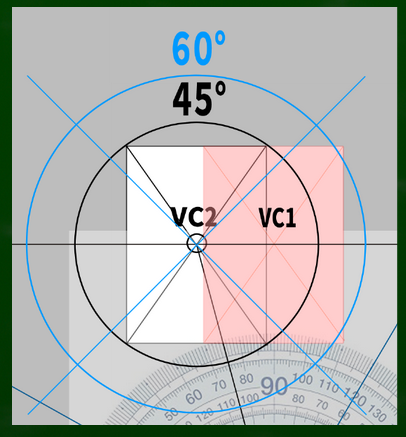
たとえばVC2を視心とした場合､VC1を視心としていた画面は45度視円錐の範囲に収まらない｡

60度視円錐の範囲にギリギリ収まるかどうかというところだ(視円錐はVC1を基準に作って移動させたが､もしかしたら違う方法でつくるのかもしれない)｡60度でも二点透視図法は問題ないので､もし右側の画面を構成したとしても絵を描く際に大きな問題はないといえる(前提が誤りでなければ)｡

前提の中で重要な問題は以下の２つである｡

頭を左右に傾けた場合､視線が変化し､視心も変化するかどうか｡
もし視心が変化した場合の視円錐はどうなるのか｡そもそも画面を一定の位置まで動かしてしまうと､実質的に動かす前と同じような見え方になるのではないか｡※もちろん､画面を動かすことによって､動かさなければ見えない範囲の対象が見えたりするという違いは生じるが､その点は除く｡

今回は視心が変化すると仮定して進めた｡今までは視心が変化しないと仮定して進めていた｡

｢特にこだわりがないのであれば､水平線上かつ画面の中央付近に視心を置くのが無難｣だと説明しているサイトもある(パースフリークスさん｡ただし､なにかを描き始めると視心の位置は任意ではなくなるようだ)｡

そもそもの重要事項は｢対象をどのように見せたいか｣である｡

第一に､45:45では見えない範囲に対象があるなら､カメラを移動させずにカメラを左に傾けたり(回転)､カメラごと移動させる(もしくは対象を移動させる)ことで､対象を捉えることができる｡

その場合､｢新しい画面｣を構成する必要があり､その新たな画面に視心をとっていくほうが整合的に把握できる気がする(対象を動かすなら同じ画面でもいい)｡視線が変化したのに視心が変化しないというのは､直感的に違和感がある(パースが歪まないとしても)｡

第二に､45:45では見える範囲に対象があるが､｢違った角度で見せたい｣というケースが考えられる｡

たとえばサイコロを真正面ではなく､角をメインに見せたい場合である｡この場合､カメラを移動させずに回転するだけではよく見せられない場合が多い(見せたかったサイコロは画面の右か左端に寄ってしまったりする)｡したがって､カメラを移動させる(左右に回り込むように)か､対象を物理的に回転させる必要があるかもしれない｡

もちろんこうした移動の思考は３次元の話や３Dソフトだからできる話だが､二次元の場合もこういった｢どう見せたいか｣という思考過程が重要になる｡その思考過程次第では画面の構成が変化するのであり､その変化のために消失点の位置や立点の位置を変化させる必要がある｡

ようするにこれは｢センス｣の問題でもあり､｢構図｣の問題であると言える｡｢対象の角を見せるべきか､見せないべきか｣といった項目にパースの技術はなにも答えてくれない｡パースは｢もし見せたいなら､こう設定するべき｣という答えをくれるだけである(理解するのに苦労するが､客観的な正解が数学のようにパースにはある)｡

【補論】２点透視図法で段ボールを描く(COV2のケース)

※COV2とは､45:45の視円錐をCOV1ではない､60:30で新たにできたCOV2のことである｡さらに､視心や画面もそれに伴いズラしたケース｡

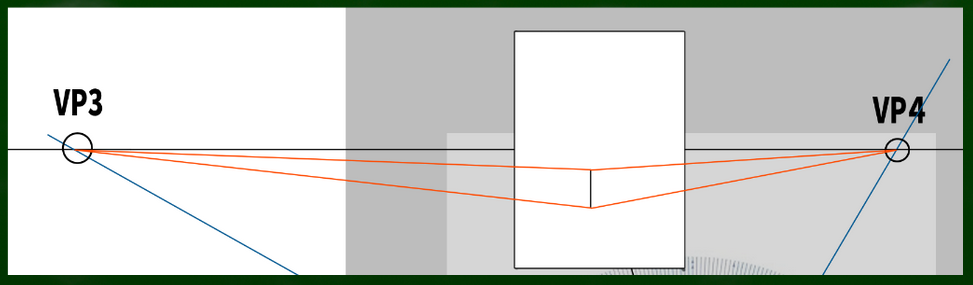
まずは適当に垂線を引く｡

次に､各VPへと線を伸ばす｡

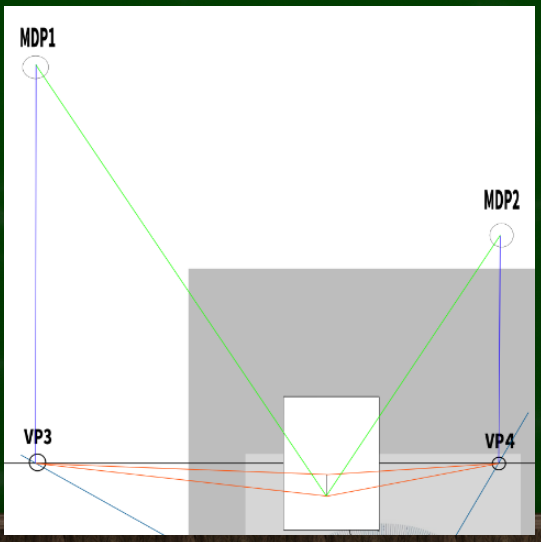
MDP(介線点)へと線を伸ばす(詳細は第六回の記事を参照)｡

【第六回】パース基礎:｢二点透視図法で立方体を作成する方法｣を解説

MDPから得られた奥行きの指標点を参考に､立方体を構成する｡

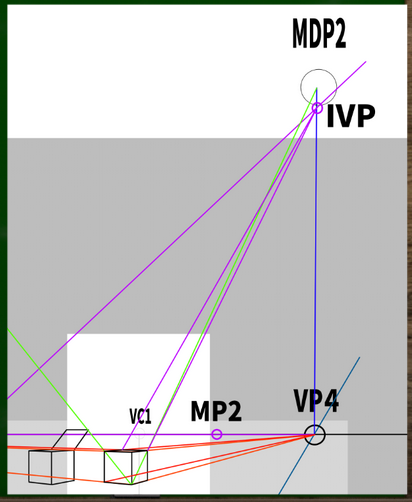
MP(測点)を利用して傾斜消失点(IVP)を探していく｡IVPはMPから45度の斜線をVPの真上に来るまで伸ばしていけば見つかる｡

なぜ45度なのかというと､今回は段ボールの蓋の斜線の角度が45度だからである｡※MPについては第六回の動画参照｡VPからSPへの線をHLへと移行させた位置にある点である｡

次に､蓋がつく箇所から､IVPへと線を伸ばしていく｡

問題はどのくらいの高さにしたらいいかである｡さきほどの一点透視図法でやった同じ方法を今回はとる｡もしかしたら階段で作成した方法のほうが簡単にできるかもしれない｡

今回は45度の線がおよそ0.707倍になるという数学の知識を用いる｡※1×sin(45°)

二点透視図法において､縦の線(垂線)は基本的に収束しないので､定規で測って構わない｡もし10センチならおよそ7センチの位置を､もし5センチならおよそ3.5センチの位置をマークすればいい｡

そこから消失点へと線を伸ばしたときの交点が､段ボールの蓋の高さとなると仮定する｡

きれいにしたものがこちら｡

【補論】２点透視図法で段ボールを描く(COV1のケース)

COV1のケースとは､画面を左にずらさないで､60:30の二点透視図法で構成したケースである｡

同じように､まずは適当な垂線を引いていく｡

各消失点へと線を伸ばしていく｡

先ほど作った同じMDPへと線を伸ばしていき､奥行きの指標点を見つけていく｡

奥行きの指標点を基準にして立方体を構成する｡

蓋の付け根からIDPへ向かって線を伸ばしていく｡

先ほどと同じように45度の線がおよそ0.707倍になるという数学の知識を用いて指標点を探し､蓋を完成させる｡

綺麗にするとこのようになる｡

【補論】３次元ソフトと２次元ソフトの一致について

COV１とCOV２の２つの段ボールを描画して分かったことがある｡

まず､｢そもそも画面を(同じような角度になるように)動かしてしまうと､実質的に動かす前と同じような見え方になるのではないか｡｣という第２の疑問の答えの一端が分かった気がする｡

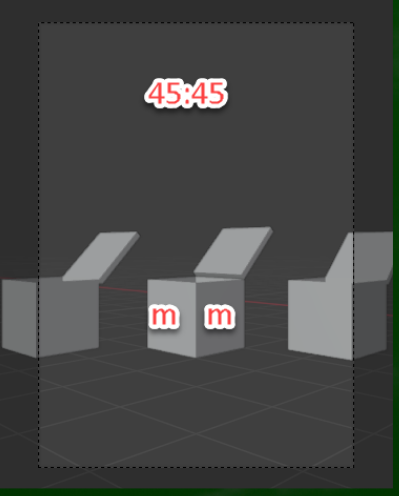
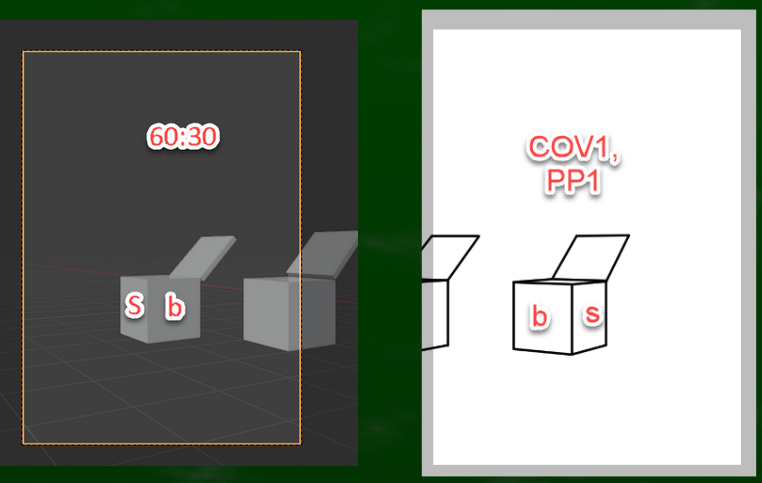
45:45(左に45度､右に45度の二点透視図法)から見えるblenderでの景色がこのようになる｡

画面の中央近くに立方体があれば､左右に綺麗に見える側面が均等に分かれる｡言語化すれば､中(middle,m):中(middle,m)である｡

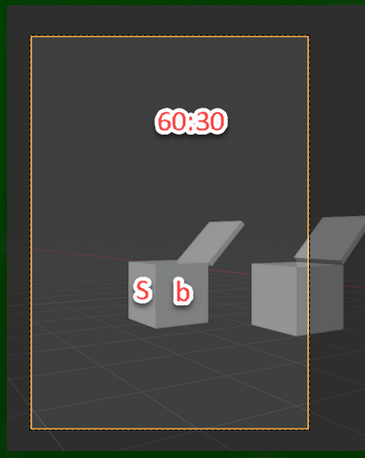
15度左にカメラを回転させると､画面の中央近くに映る立方体は小:大(small,s:big,b)であることがわかる｡つまり､右側の側面がより大きくみえるようになったということである｡

｢そもそも画面を動かしてしまうと､実質的に動かす前と同じような見え方になるのではないか｣という疑問はblender上においては｢NO｣ということになる｡

なぜなら､15度左にカメラを動かしても､動かす前の見え方である中:中には見えていないからである｡要するに､blenderでは画面を変動させても(カメラを回転させても)視心が変動していないという仮説を立てることができる(ただし､視心が変動しないなら視円錐はどうなっているのかという点は曖昧なままになる｡設定上は45度視野角､焦点距離43.46mmは維持される)｡

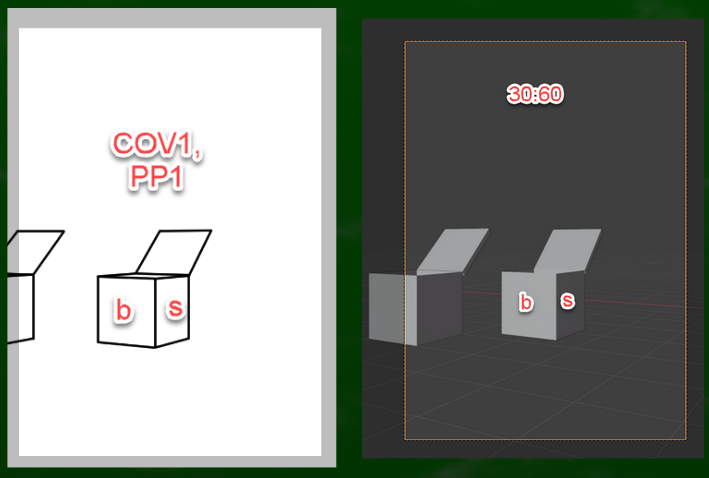
しかし２次元ペイントソフトの場合(３次元のアナログ描画も同様)､画面を左に移動させると､視心までもが変化してしまうようにみえる｡

なぜなら､60:30のケースにおいて､画面の中央付近に中:中の立方体が見えるからである｡

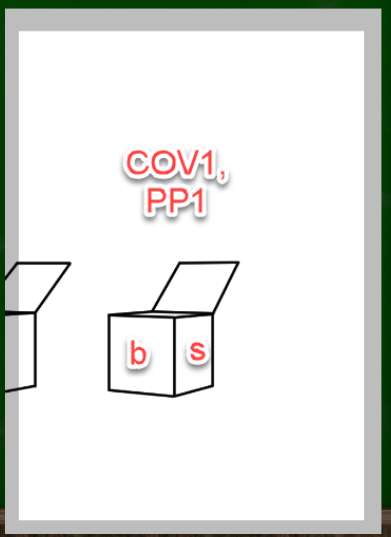
一方で､画面を新たな視心に合わせて移動させない場合の図がこちらである｡要するに､消失点を変更したが､視心の位置や画面の位置を変えなかったケースである｡

中:中の立方体が現れていないという点がポイントである｡

中:中ではなく､大:小が現れている｡視心は変わっていないが､消失点が変わったことによって､見え方に変化が生じていると仮定できる｡

しかし､blenderにおける左に15度カメラを回転させたケースと､側面の見える大きさの割合が逆である｡

カメラを45度から15度左に動かすのではなく､15度右に動かすことによって､２次元ソフトと同じような画面が現れた｡

blenderとペイントソフトで角度の考え方が違うのかもしれない｡なぜ違うのか､その原理はまずは保留しておく｡

ペイントソフトでは青色の部分の60度を私は使い､左右に60:30などと表現していた｡blenderの場合は紫の部分の30度を使うのかもしれない(あるいは右側の30度)｡

２次元ソフトでパースを描いていて度々感じることは､｢このパースは本当に正しいかという不安｣である｡

この不安を減らすためには､３次元ソフトで２次元ソフトと同じような画面を常に構成できる必要がある｡そのために今回はその実証を行ったというわけである｡｢どのような絵でもいいからパース的に正しい絵を描くこと｣に加え､｢見せたい絵に合わせたパースを自由に配置すること｣をマスターするとパースの幅がぐっと広がる気がする｡

３次元ソフトで画面を動かしているだけでは得られない３D感覚の知識(身体知)というものがきっとあると考えている(3Dのトレースだけでは学べない)｡

次回の予定

三点透視図法におけるダンボールのケースを扱う(おそらく)｡

※チャンネル登録をしていただけると更新頻度が上がるかもしれません！協力よろしくお願いします！

参考文献

初心者でもわかりやすい本

ロビー・リー「超入門マンガと図解でわかる! パース教室」

・パース全般の基礎において一冊目にこれを手に取るのに適している｡・私は「パース！マンガでわかる遠近法」よりも平易に､かつ丁寧に説明されていると感じた｡それゆえに､初心者は特に一冊目にこの本をおすすめする｡

デヴィッド・チェルシー「パース！マンガでわかる遠近法

デヴィッド・チェルシー「パース！2 マンガでわかる遠近法

・イラストが多く､わかりやすい｡パースの基礎用語の説明もされていて､かつ平易にパースの使い方が説明されている良本｡ただし､建築パースに特化しているわけではなく､「イラストレーション(漫画)」に特化している点を注意する必要がある｡・パース全般の基礎を学ぶという目的において一冊目にこれを手に取るのに適している｡

上級者向け

「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」

絵を描く､特に線画に特化した本｡小難しいが広く､深く説明されている良本｡

山城義彦「現代パースの基本と実際」

・パースの歴史や細かい用語が説明されていて便利｡ただしメインはイラストレーションではなく「建築パース」に特化している点を注意する必要がある｡・かなり小難しく説明されている(建築パースゆえにそうならざるをえないのだろう)｡例えるなら文系が理系の数学を見たときのあの感覚に近い｡建築家ならば通らなければならない道ではある｡ただし､この本はだいぶ古く､現代ではコンピューターグラフィックスをもっと多用して楽をするのだと感じた｡ただし､楽をするにもその原理を知っておいて損はない｡