はじめに

他の前提記事について

記事が長くなってしまい複数に分けることにしました。解剖学・構造・グリッド理論の3つに分けて多角的に鼻の描画を捉えていきたいと思います。今回は2つ目の「構造」です。

構造は比率ではなく、傾向のほうが近いです。グリッド理論で比率は検討していきます。なぜ陰影がつくのか？なぜそういう線になるのか？という「根拠」をすこしでもつかむ作業です。

この記事は手探りで問いを立て、仮説を立て、検証しています。わかっているものを記事にしているわけではないので正確性は保証できません。つまり、単なる思考過程のログです。

※この動画は3dcgで鼻を作るというものではありません。しいていえば鼻のアタリを分析する作業です。

絵を描くための鼻の解剖学知識

鼻の解剖学についてはこちらで説明しています。

第５回：グリッドで人間の横顔を描く方法について考える-鼻の描き方

側面の鼻についての考察はこちらです。

【blender備忘録】眼をモデリングする方法のテスト①

鼻の3dcg制作についてはこちらで説明しています。

鼻の構造の最小構成要素を考える

仮に錐体がシンプルな構造だと想定してみます。錐体の中でも、三角錐の場合と四角錐の場合があると思います。

三角錐的に考えてみます。三角錐とはすべての面が三角形だということです。

 

次に四角錐的に考えてみます。

©福本 伸行 「賭博堕天録 カイジ 24億脱出編」より

どこかでこういう鼻見たことあるなあ、と思ったらカイジの鼻でした。

同じ三角錐でも、どの面を前にするか、後にするかとった違いがあるかと思います。

 

両方を見れば分かると思うのですが、要するにとがったほうが前にくるか、面が前に来るかといった違いです。カイジの鼻はとがったほうが前にきた形に近いです。

花の構造としてどちらが適してるか？という問題なれば、やはり前にとがっている方が来るケースですね。

つまりこのケースです。実際にここまで鼻(つまり鼻梁)がとがっているわけではなく、一定の幅をもちます。それが後で登場する「上面」なわけで、それが四角形を構成するというわけです。

構造的に言えば、三角錐に四角形を加えた、つまり四角錐に近いわけです。さらに進めれば、鼻尖と二つの鼻翼、つまり３つの球体を加えることになるかと思います。

しかしもっともシンプルなモデルは三角錐であると仮定していいと思います。

三角錐とは

・三角錐(さんかくすい,triangular pyramid):垂直断面に三角形をもつ錐体のこと。錐体とは、空間内の一点から底面に伸びる線分によって形作られる錐状の立体図形の総称。

出典

錐とは？と不学な私はよくイメージできませんでした。錐(きり)とも読み、板状に穴をあける工具だそうです。たしかに先端が三角形みたいなものがありますね。三角錐、四角錐といういろいろな錐体がありますが、どれも三角形を含んでいます。

出典

これがいわゆる三角錐というやつらしいです。ようするに錐とはとがっているということです。全て三角形でできていたら三角形、四角形もまざっていたら四角錐というわけですね。

鼻で重要なのは底面が三角形かそれとも四角形かという話です。

三角＋四角モデル

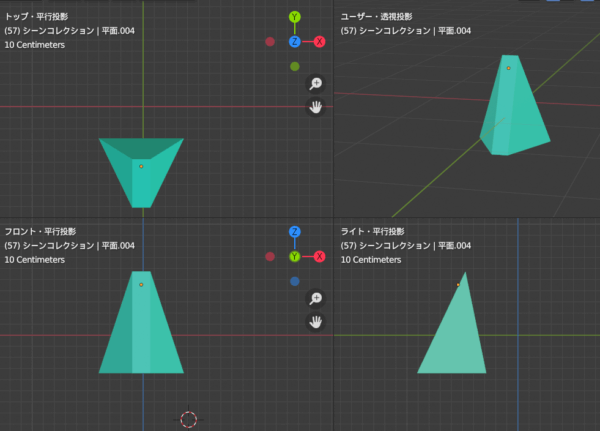たとえば鼻橋を四角形的に考えて構成しすると、底面は台形になります。側面は三角形、後面は台形となります。

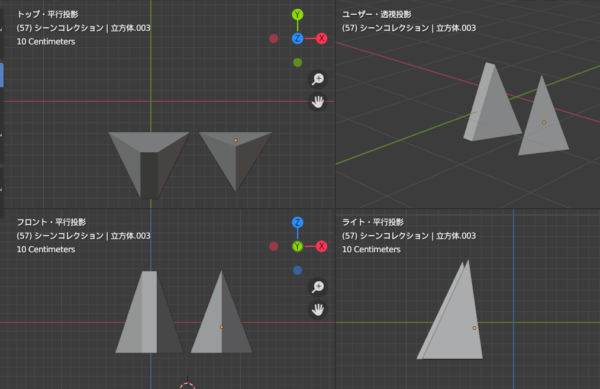さきほどの三角形のシンプルモデルと簡易的に比較するとこうなります。ここで得られる気付きはたとえばやはり上面が一番明るく、底面が暗くなるということです。光源が左にあった場合は、右側の側面のほうが暗くなります。

視覚できるということは、光があたっているということです。暗いけど見えるということは、光が弱くあたっているということになります。懐中電灯を照らしてみても、すべてのものが明るく見えるわけはありません。近くのものが一番明るく見え、遠くにいけばいくほど暗く見えます。

これらのモデルでは「底面」をよくつかめていません。

ちなみにですが、遠近法の効果が加わると、このようになります。遠近法は右上です。左下がただの平行投影です。物体としては”同じ”高さにありますが、人間の見え方としては”違う”高さに見えます。遠くにあるものほど「低く」見えるというわけです。手のひらに富士山がおさまるようにです。この奥行きの違いで、立体というものは表現されるわけです。遠くのものは低く、小さく、あるいは色が薄く見えたりします。

したがって、立体感というものは「陰影」と「遠近法」が関係してくる項目と言えます。他にも色だったり、他にも心理的なものだったりと様々な「立体感を生じさせる要素」はあると思います。しかし「陰影」と「遠近法」はとりわけ重要なものです。

三角＋四角＋丸モデル

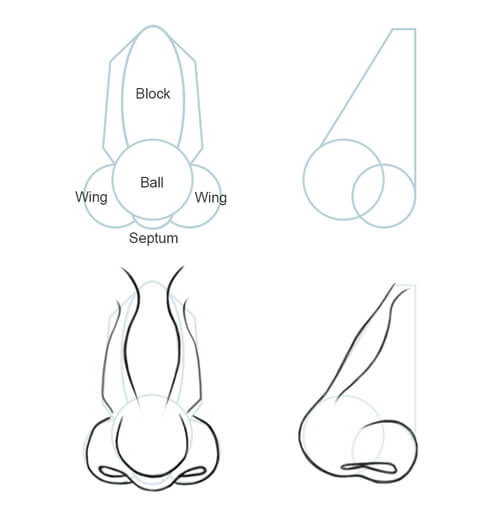
鼻には３つの球体がある、とよくいわれることがある。実際に球体を３つ描いて鼻を描く方法もある。

出典

たとえばこのサイトも同じような考えをしている。

まず当然なのに自覚できない問題が二次元にはある。ボールを３つ並べられても、どれが前だか後だか「意識」できない。無意識にはわかってるはずなのに、描いているとどっちがどっちだかわからなくなってくる。それは当たり前の話で、二次元だと全て奥行きだからだ。絵というものはこの同じ奥行きを違う奥行きであるかのように見せる方法であるといってもいい(もちろん表現の一つにすぎないが)。それは大きさで表現したり、陰影で表現したり、薄さで表現したり、色で表現したりする。

鼻の３つの球体が仮に同じ大きさであったと仮定しても、鼻翼の球体のほうが「後ろ」にある。つまり三次元としては奥にある。したがって、遠近法的には前の球体よりは小さく見える。しかし経験的に言えば、ある物体とある物体の距離の差が小さければ小さいほど、その大きさの差の「見え方」も小さくなる。

鼻の3つの球体の位置はとても近い。したがって差もわかりにくい。であるのにも関わらず、やはり鼻翼のほうが明らかに小さく見える。

ということは、3つの球体が「同じ大きさ」であるという仮定のほうが間違っているのかもしれない。つまり、3つの球体の中で、中央の球体のほうが物理的に大きいということである。

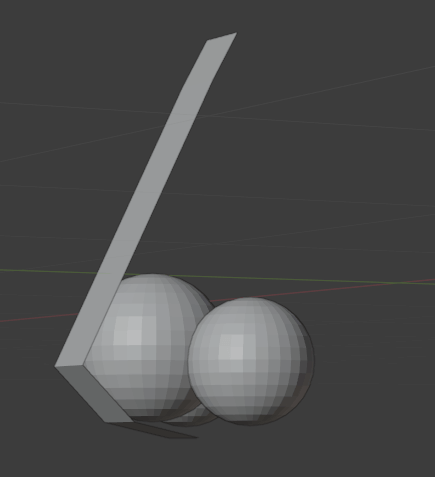
実際に球体を仮設してみたが、やはり中央の球体が左右の球体よりも物理的に大きいといっていいと思う。

さらにそれぞれの球体は前から見ると重なる部分が多い。

直線では捉えきれない、鼻中隔へ向けての奥行きの移動が球体だと様々な段階を含んだ移動として表現可能になる。

直線で簡易的に作ると3段階の変化しか表現できないが、球体だと考えると段階の数が何倍にも増える。

あとの作業は、比率を確定して、どのくらいの幅で、どのくらいの大きさの球体や錐体、台形等を設置すればいいのか？という「比率」の問題になる。

構造としてはすでに、鼻は「三角＋四角＋丸」であるという一定の回答ができていると思う。三角だけ、四角だけ、丸だけでも表現可能であるが、合わさることによってさらに鼻としての立体感が出る。

出典

線画の構造としてはこちらも参考になる。

出典

こちらは３つの球体ではなく、直線と小さな球体として考えている。これはこれで面白い。

 

メモ

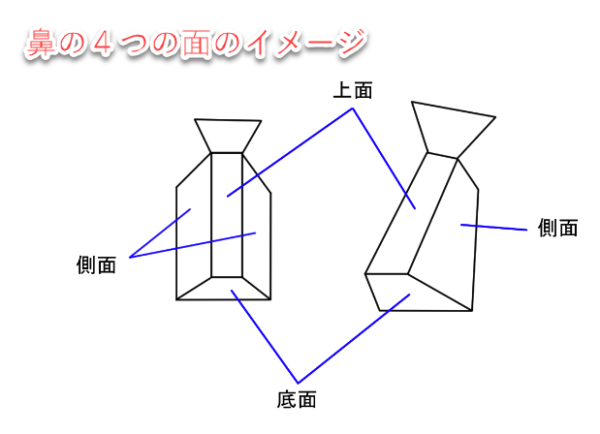
面の構造

いわゆる上面・側面・底面の3つの要素にわける考え方です。側面は左右に２つあるので、合計4つの面から鼻が構成されます。オッカムの剃刀のように、複雑なものも本当に必要なものだけに分解するべきなのかもしれません。

実際の鼻はもっと複雑です。しかし理解するには情報が多すぎます。シンプルな理解はやはりシンプルな要素が必要になります。もっとシンプルにすれば三角錐に近づくのでしょうが、実際はもうすこし四角に近いのかもしれません。

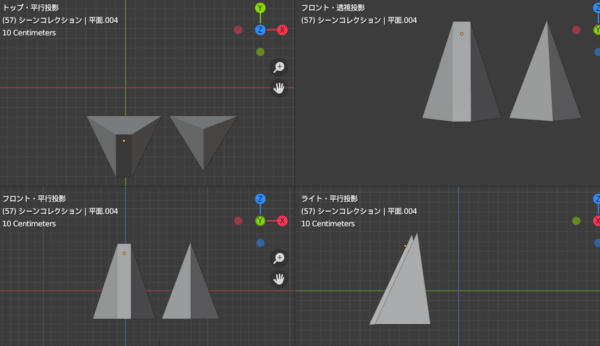
モデリングしてみると、おおよそこのような外観になります。

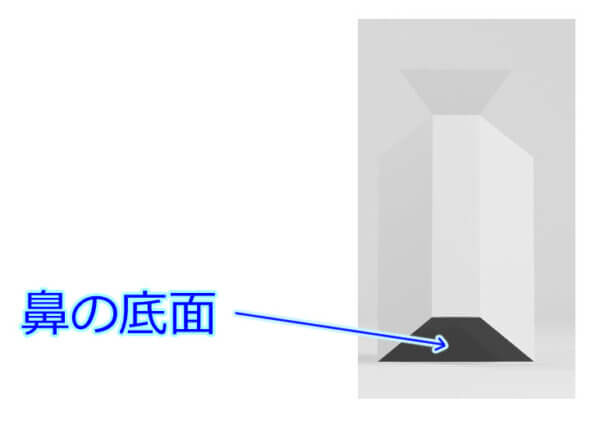
鼻の底面の分析

なぜ鼻の底面は陰が濃いのか

これが鼻の底面です。陰が濃くなっていることがわかります。

構造的な理解で重要なのは「なぜ陰が濃くなっているのか」です。新規

晴天の日に外にでかけて、日傘をさすとその下には濃い影ができます。日傘が遮光物(しゃこうぶつ)となっているのです。鼻の底面で陰ができているのは、なにかが遮光物、つまり光をさえぎっているためだと考えられます。

なにが遮光物なのか。よくみると、鼻の上面や側面が光を遮っています。

例えば傘を鼻の上に置いてみます。底面にできていた陰と同じような濃い影が傘の影によって鼻の前面や側面にできます。

このことからも、遮光物によって底面に影ができていることがわかります。

なぜ底面が側面で見えないのか：頂点思考と軸思考について

単純な構造まで分解すると、鼻を側面から見ると底面が見えません。実際の鼻はもう少し複雑なので底面が見えますが、そのことは今は置いておきます。

なぜ見えないのか。自分で問いを立てて、考えていく作業はとてもおもしろいです。

3dソフトでは頂点、面、辺という３つの基本的な要素で考えます。この考え方を、2dの絵でも活用します。

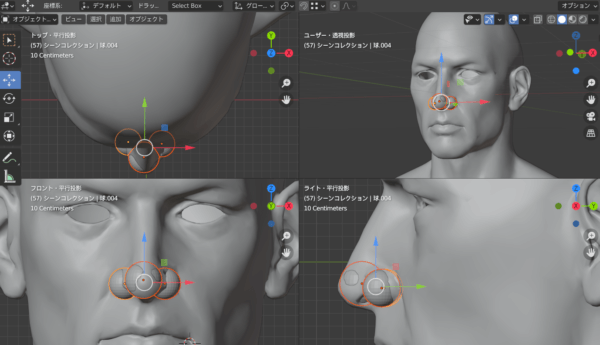
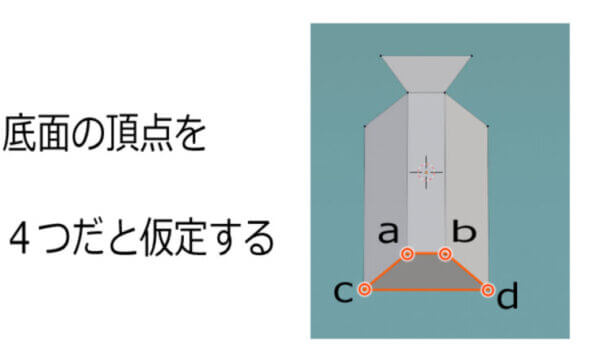
今回は「頂点」を利用します。シンプルな鼻の構造の底面には４つの頂点があります。

頂点理解で重要なのはX,Y,Zという3つの軸です。それぞれ幅、奥行き、高さを意味しています。

二次元的な理解では、奥行き(Y軸)が同じかどうかがわかりにくいです。たとえば上の画像でいうところのaとcの奥行きが同じかどうかぱっとみではわかりにくいです。aとcが同じ高さかどうかもわかりにくいです。aとcが違う幅にあるということはなんとなくわかります。

二次元的な理解で奥行きを示すポイントは、パース(奥に行けばいくほど小さく見える)と陰影です。これは基本的ですが、超重要だと思います。失念しがちです。

たとえばaとcの奥行きが違うということは、二次元的な絵でも「陰」によってわかります。底面は他の色より色が暗いですよね。

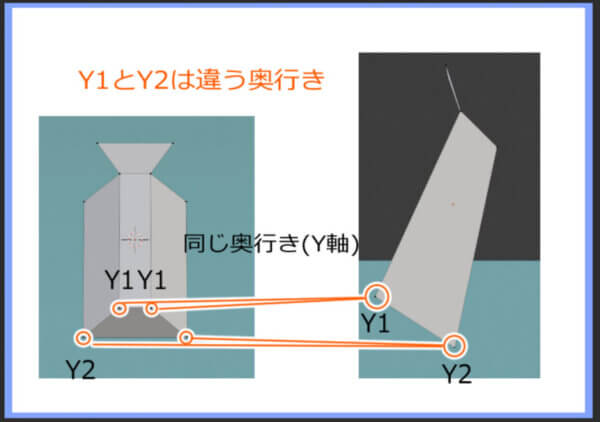
奥行きが違うことは、側面で見ると二次元的な理解でもよくわかります。

Y１のほうがY２より手前にあります。aとbは同じ奥行き(Y1)であり、cとdは同じ奥行き(Y2)であるということがわかります。同じ奥行きなので、ちょうど側面から見た場合に重なり、頂点が合計２つしか見えません(acかbdのみ)。

また、Z1とZ2でもZ軸(高さ)が違います。

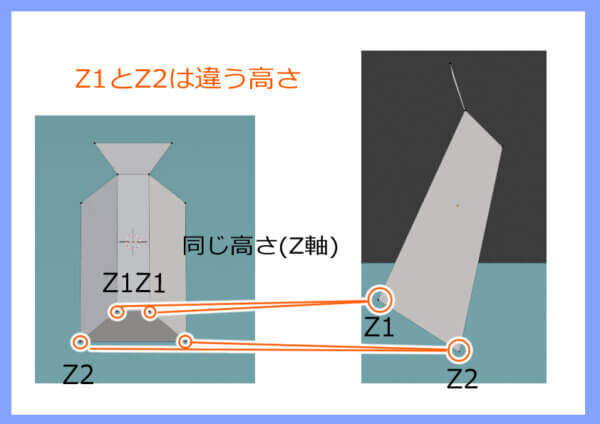
もし仮に高さがZ１＝Z2出会った場合、側面及び正面の図はこうなります。

Z軸が同じでも、パースがかかるので同じ高さには見えません。これは実際の物の座標ではなく、我々人間の視点によって起きる現象です。

近くにあるものは大きく、高く見えます。遠くにあるものは小さく、低く見えます。先程の図で言えば、Z1のほうが手前にあるので高く見え、Z２のほうが奥にあるので低く見えているということです。

この記事はパースの記事ではないので、パースの説明はこの辺にしておきます。

構造理解において重要なのは、なぜ正面において底面が見えるかを言語化することです。

４つの頂点が仮に全て同じZ軸にあると仮定した場合、正面で鼻の底面は見えませんでした。したがって、正面で底面が見えるかどうかは、Z軸が関係していると推測できます。つまり、手前の頂点と、奥の頂点の高さが違うことが関係しているといえます。手前のほうが高く、奥のほうが低い場合に段差が生じ、底面が見えるということです。

鼻の底面が台形に見えるのはなぜか

台形とはなにか

・台形(だいけい,trapezium):四角形の一部で、少なくとも一組の対辺が互いに平行であるような図形である。平行な2本の対辺を台形の底辺といい、そのうち一方を上底（じょうてい）、他方を下底（かてい）とよぶ。また、もう一組の対辺を台形の脚（きゃく）とよぶ(WIKIより)。1本の底辺の両端の内角が互いに等しい図形を「等脚台形」という。

今回使った鼻の底面は、台形です。さらに脚も左右対称で等しいので、「等脚台形」です。

パースによって台形に見えている、というような話ではないです。

軸思考で考えると、四角形と台形の違いは何か？という観点から考えてみたいと思います。厳密に言えば台形も四角形なのですが、ここでは細かいことはおいておいきます。

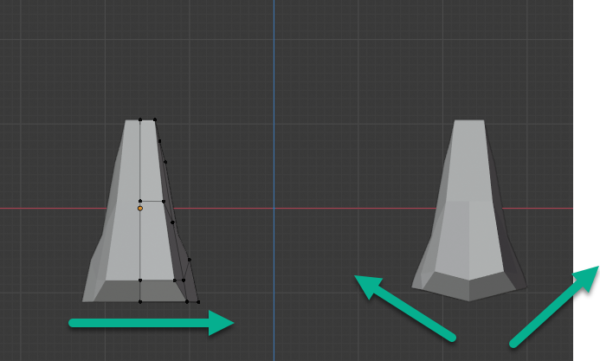
こういった仮定で重要なのは、一度作ってみることですね。底面が台形ではなく、長方形だった場合を想定してみます。

変わった軸は、X軸です。つまり幅です。台形の用語でいうと、上底の幅の長さが短くなっています。

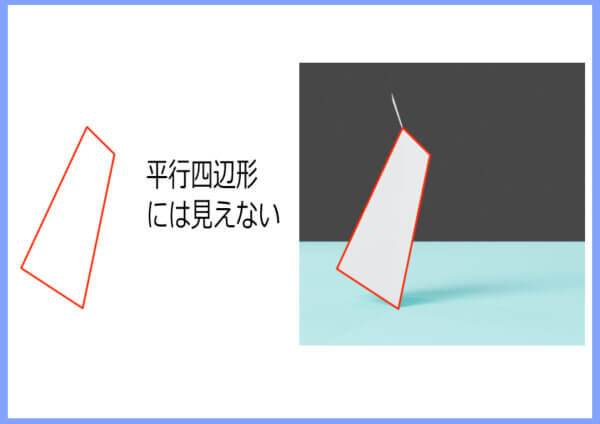
側面は平行四辺形の形をしているか？

簡易モデルの場合は正面から見ると平行四辺形の形をしているように見えます。

しかし側面から見ると、平行四辺形には見えません。

正面からは平行四辺形に見えるのに、側面では見えないのはなぜでしょうか。

そもそも鼻の解剖学的には、鼻翼が一番幅をもっているはずです。

こういうときは側面でも平行四辺形のオブジェクトを作って比較するほうが手っ取り早いです。

正面ではなぜ違いがわかりにくいのか？と問いをたてて考えてみます。答えは「奥行き(Y軸)」の変化だからです。たとえば鉛筆を自分の目の前にもってきて、自分の方に向けてみてください。鉛筆の先が奥に向かってどんどん伸びたとしても違いには気づきにくいはずです。鉛筆を横にして初めて、長いな、と目視できるはずです。

鼻は三角形か？

側面が平行四辺形的ではないということは、なにか意味があるはずです。それはなにか。鼻というものが、上にいくにつれて幅が短くなっていくからです。これは仮定です。

 

たとえばこのように形を想定してみます。イメージで言うと三角形です。先程より上部のX軸が狭くなっており、Y軸も狭くなっています。

リアルな鼻を重ねてみると、やはり構造としては三角形に近いはずです。

出典

こちらの簡略化画像を見ても、やはり三角形に近いです。左と右にふたつの簡略化(SIMPLFIED)がありますが、右側のほうがX幅が上に行くほど短くなっているようにみえます。

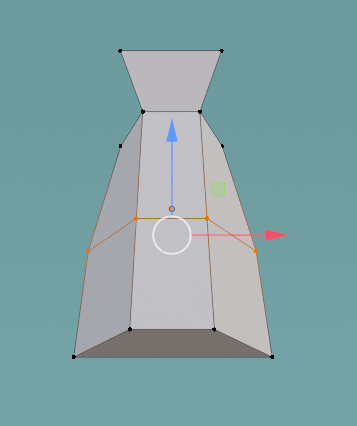この画像だと右側の鼻は、中間で少し幅があります。つまり、三角形というよりひし形に近い感じになります。もし仮に側面を三角形として構成すれば、より錐体に近づきます。

切断された鼻

簡易的なモデルをリアルな鼻に当てはめてみると、「重ならない部分」が出てきます。

とりあえずそれはおいておいて、単純モデルをもうひとつ考えてみます。

あ、ちょっとホラーっぽくなってしまいました。

直線上だけとりだすとこうなります。グレースケールが３段階のものだとすれば、薄い、中くらい、濃いの三段階です。あるいは上面、側面、底面といったかんじでしょうか。

二次元的な画像の中で何が立体を立体足らしめているか？そのひとつの要因が「陰影」です。この境目が３段階しかない、というのがポイントです。あくまでも簡略化するとですが、いちおう考察に値するかもしれません。

さてこうした陰影はなぜ発生するのでしょうか。上のものが「遮蔽物(しゃへいぶつ)」になっているからでです。光を遮っているわけです。要するに傘理論です。

しかし実際はもっと「丸み」を帯びているので、平面の連続として単純化するのは限界があります。三段階の境界がもっと曖昧で、ぼんやりと移行していく感じです。もちろんこれは光源の設定によります。

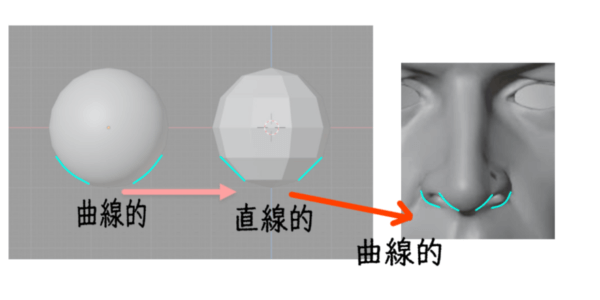
鼻の斜線性について

前回も考察しましたが、鼻は斜線的です。

しかしよくよく振り返ると、この斜線性は球体の簡易化なのかもしれません。

球体を四角形に近づけると、こうなります。

つまり鼻の本来の性質としては曲線的なのですが、簡略化させると直線的になるということです。

曲線であろうが、直線であろうが、斜線的であることに変わりはありませんね。

なぜ斜線的であることが重要かというと、斜線的であるからこそ、正面で鼻の穴が見えるからです。

実際の鼻で線を探してみると、こうなりますね。

この斜線的な線で平行四辺形あるいは楕円を作ると、中に鼻の穴を構築することができます。囲まれた中のさらに、上部が鼻の穴になるわけです。

鼻の穴も実質的には正面から見ると斜線的です。

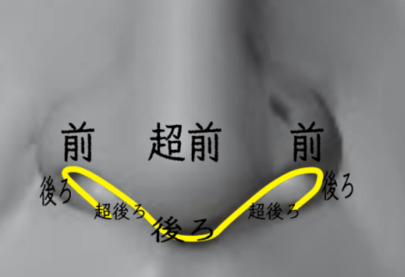
こうしてみると、鼻の穴、というより底面はある側面から見れば、M字的であるとも表現することができそうです。画像としてみればすべて同じ奥行きですが、表現としてみればこのように前後関係を想定できます。

鼻の穴はもはや肌と同じ奥行きの位置にあるので超後ろです。鼻先は顔でもっとも前にあるので、超前です。このように前後関係を概略的に把握することが、陰影付けや根拠付に力をかしてくれるかもしれません。

重要なのは、「そんなのあたりまえじゃん」といった当たり前の事実をまずは「言葉」にしてみることだと思います。その集積がひとつの経験であり、絵の上手さにつながっていくのだと思います。

参考文献

人体の描き方関連

やさしい人物画

ルーミスさんの本です。はじめて手にした参考書なので、バイブル的な感じがあります。

人体のデッサン技法 ジャック・ハムも同時期に手に入れましたが、比率で考えるという手法にルーミス同様に感動した覚えがあります。ルーミスとは違う切り口で顔の描き方を学べます。

解剖学関連

スカルプターのための美術解剖学: Anatomy For Sculptors日本語版 スカルプターのための美術解剖学 2 表情編

一番オススメの文献です。３Dのオブジェクトを元に作られているのでかなり正確です。顔に特化しているので、顔の筋肉や脂肪の構造がよくわかります。文章よりイラストの割合のほうが圧倒的に多いです。驚いたときはどのような筋肉構造になるか、笑ったときはどのような筋肉構造になるかなどを専門的に学べることができ、イラスト作成においても重要な資料になります。

アーティストのための美術解剖学

こちらはほとんどアナログでイラストがつくられています。どれも素晴らしいイラストで、わかりやすいです。文章が少し専門的で、難しい印象があります。先程紹介したスカルプターのための美術解剖学よりも説明のための文章量が圧倒的に多く、得られる知識も多いです。併用したほうがいいのかもしれません。

遠近法関連

パース!

これが一番おすすめです。難易度は中です。

超入門 マンガと図解でわかる! パース教室

これは難易度は小ですが、とてもわかりやすく説明されています。

スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く方法-

難易度は大ですが、応用知識がたくさんあります。

色関連

カラー&ライト ~リアリズムのための色彩と光の描き方~

やはりこれですかね。