楕円とは何か
楕円の定義
楕円とは:楕円(だえん、橢円とも。英: ellipse)とは、平面上のある2定点からの距離の和が一定となるような点の集合から作られる曲線である。基準となる2定点を焦点という。円錐曲線の一種である(wiki)。
(wiki)
文系の私には頭が痛くなりそうな定義です。とりあえず次へ進みましょう。
楕円の性質について
楕円は完璧な「左右対称」
楕円は左右対称で、きれいに四分割できる
たしかに先程wikiにあった楕円の図もきれいに四分割できてますね。ここがおそらくポイントです。きれいに四分割できないような楕円は楕円じゃないと。
それならきれいに4分割できる円も楕円のひとつなんじゃないかと思います。
円とは:平面(2次元ユークリッド空間)上の、定点 O からの距離が等しい点の集合でできる曲線のことをいう(wiki)。
らしいですからね。
(wiki)
楕円の楕って惰性の惰だと思ってましたがぜんぜん違うんですね。PCが低スペだと同じように見えます。
楕(だ)とは:長円形(デジタル大辞泉)。「楕」の訓読みは「こばんがた」らしいです。
とりあえず長い円の形が楕円なのだと思います。
クリスタのツールでも楕円ツールがあります。円のイメージは正方形の中に収まるようなきれいな円のイメージでした。このようなきれいな円は楕円というよりも「正円」といったほうがいいかもしれません。正円とは完全な円を意味します。もちろん正円も楕円の一種です。現実世界でこんなきれいな正円少ないですよね。あったとしてもパースで楕円に見えてしまうことが多いと思います。
そして楕円は長い形をしているイメージで、かつきれいに四分割できないといけません。
さてこれは楕円でしょうか。
楕円だと思います。四分割できそうです。四人兄妹でも不平不満が起きないでしょう。横に長いので円というよりは楕円です。
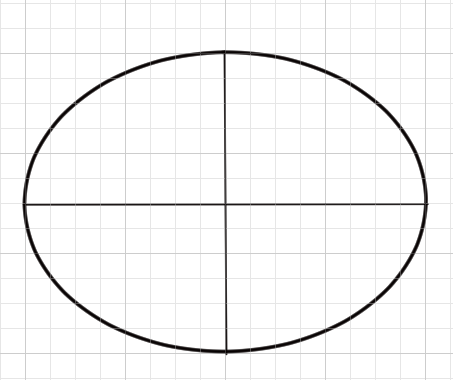
ではこれは楕円ですかね?
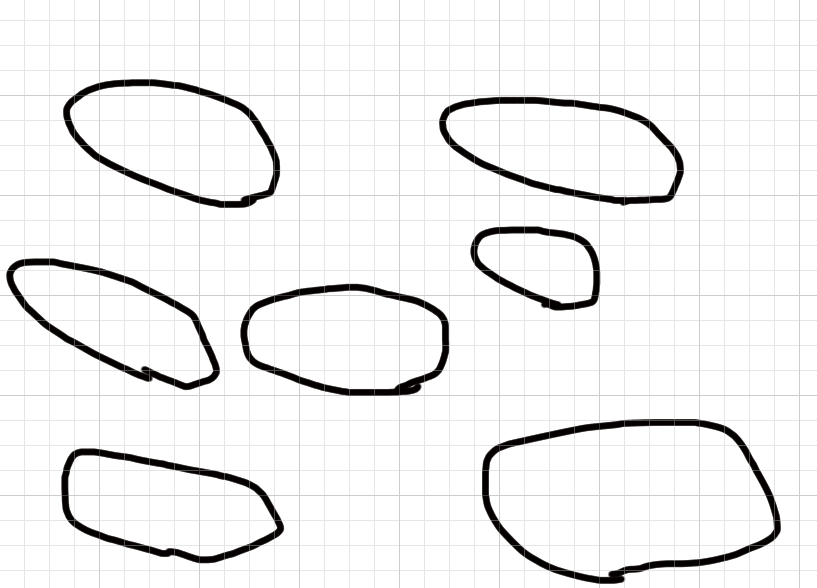
これはおそらく楕円ではないですね(笑)。4分割が難しそうです。
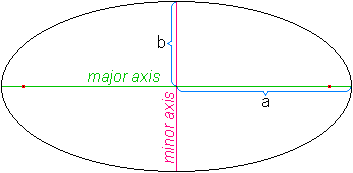
楕円の長軸と横軸を使った楕円の描き方
楕円には長軸と短軸というものがあります。また、楕円は2本の軸によって左右対称に分割されます。
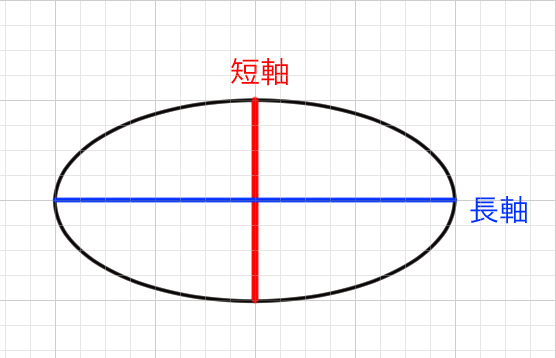
2本の軸のどちらが短軸か、長軸かという分類は線の長さによって決まります。そのままですが長いほうが長軸です。上の図のとおりです。
楕円が2つの軸から形成されるということがわかれば、2つの軸さえ設定できれば楕円はかけそうな気がします。
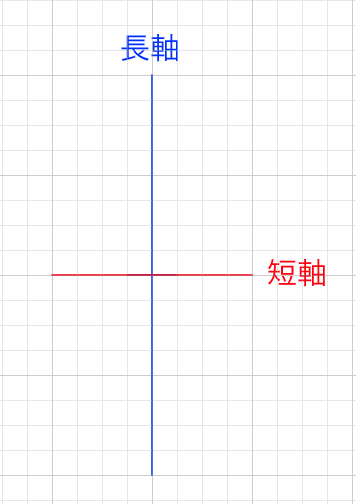
長軸と短軸を設定するときは、お互いの軸の半分の位置で交わるようにしましょう。そうしなければきれいに4分割できません。
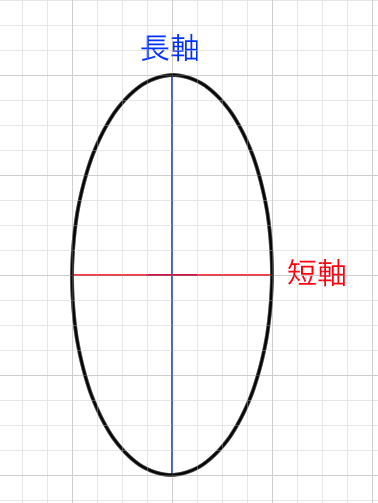
今は手元にマウスしかないので線が揺れてしまいますが、ましな楕円がこの法則によって描けるようになります。アナログできれいな楕円を書こうとするときもこの法則は便利です。
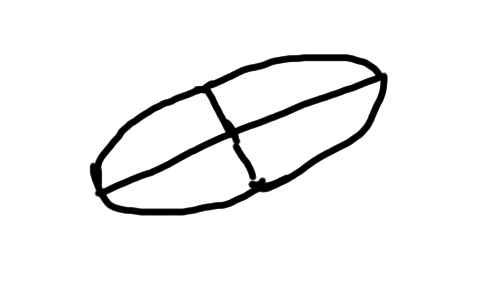
楕円は尖った部分や直線部分がありません。それを念頭に置いて楕円を描きましょう。
楕円とパースの関係
楕円の中心と正方形の中心はぴったり合わない
【前提知識】一点透視図法で正方形や立方体を作る方法
まずは正方形を一点透視図法を使って描いてみます。
視円錐についての説明やパースで正方形や立方体を構成する記事は以下にありますので参考にしてください。
今回は対角線の消失点を画面外に置きます。画面内では45度の視円錐になるように設定します。画面外の視円錐90度の位置に対角線の消失点を置きます。
また、キャンパスサイズA4の場合は最初から横幅を842の2倍、つまり1684ピクセルで設定します。これはクリップスタジオペイントのパース定規がデフォルトで画面の端に設定されることを利用したものです。1684ピクセルで設定すると、A4画面内がちょうど45度の視円錐になるように設定できます。
これが初期位置の一点透視図法と二点透視図法の消失点です。

画面の端に消失点が来ています。
幅が842ピクセルです。対角線の消失点を中央から数えて842ピクセルが好ましいです。つまり、842/2で421ピクセル先に対角線の消失点があればいいのです。
ということは最初から横幅を842の2倍、つまり1684ピクセルで設定したらいいのではと思います。
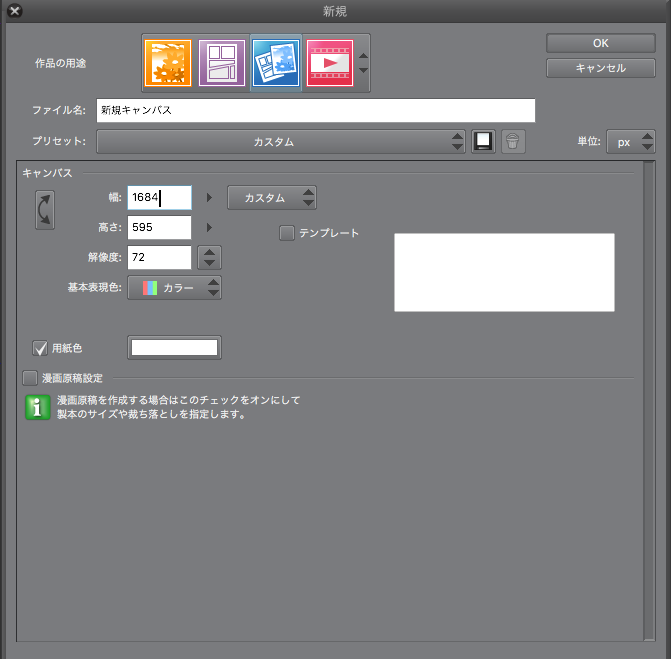
これで設定すると以下のようになります。
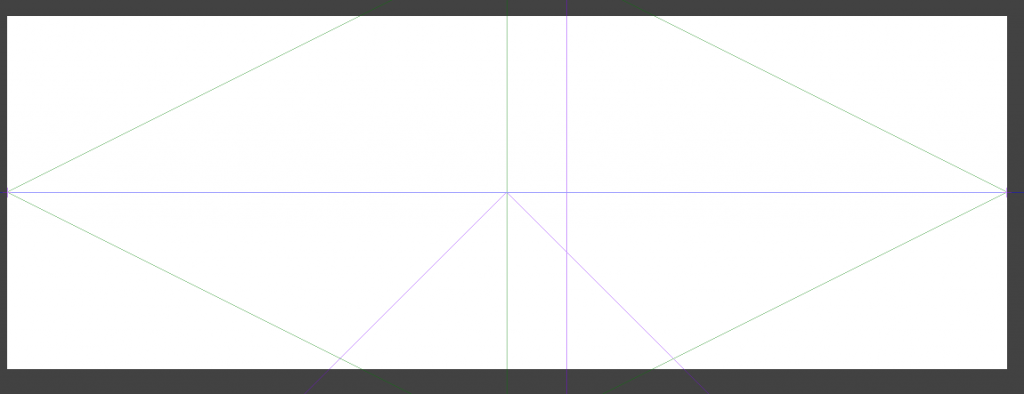
そしてキャンパスサイズの幅を842に戻せばいいのです。そうすると画面外に消失点を設定できます。
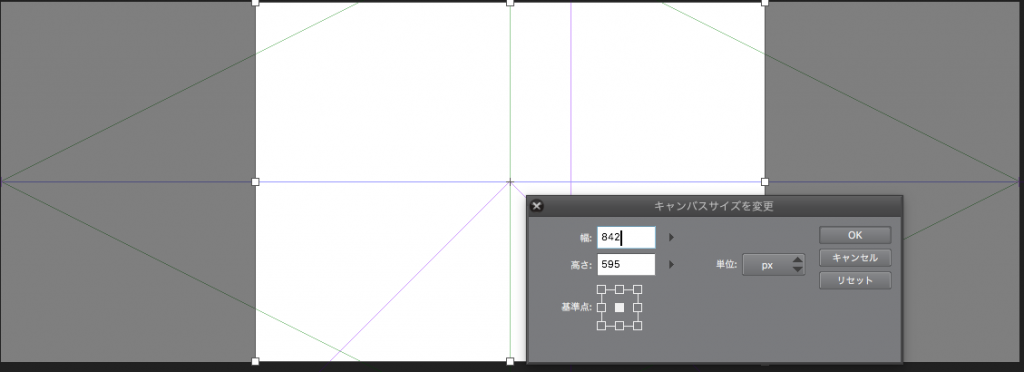
グリッドが一致して便利ですね。

このパース定規を利用して今回は正方形を作ります。
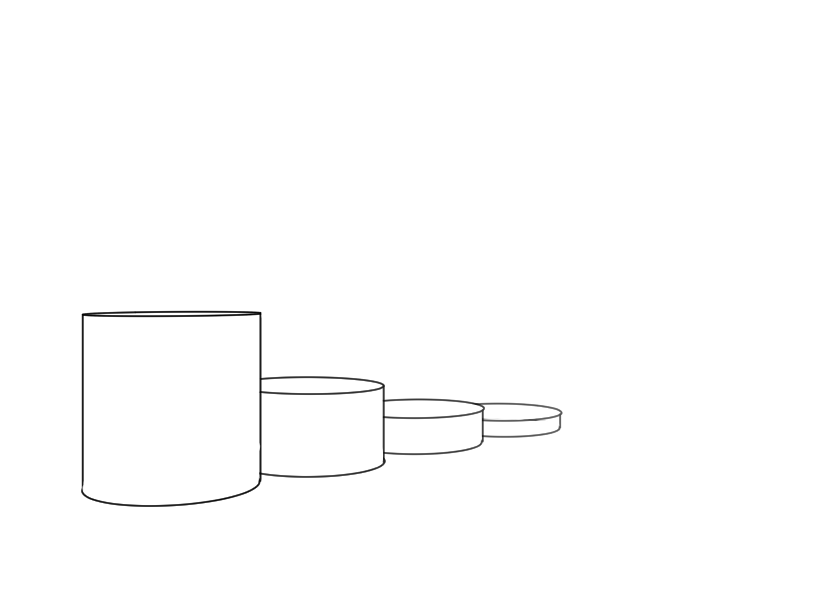
正方形を利用して円柱を作る
先程作ったパース定規のグリッドに従って正方形をつくります。グリッドサイズは50にしました。グリッドの正方形サイズの上に楕円ツールで楕円を重ねます。

円柱の高さを今回は立方体の高さとします。一点透視図法では高さは簡単にわかります。幅と高さは等しいからです。

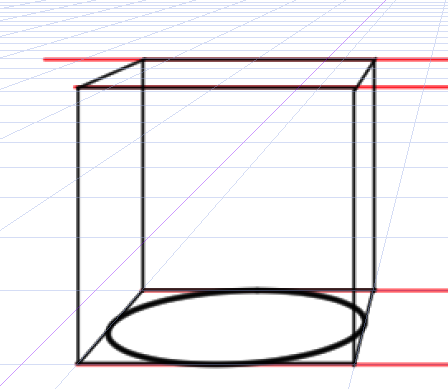
立方体の上にも円を描きます。
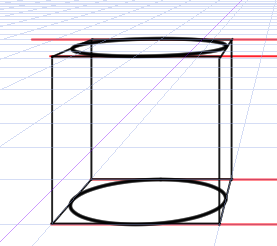
ここで問題はどのようにして2つの楕円をつなげて円柱を作成するかということです。
2つの楕円のつなげ方(なぜ正方形の中心では駄目なのか)
ためしに正方形の中心の位置で2つの楕円をつなげてみます。
この緑の線が交差している箇所がちょうど正方形の中心です。
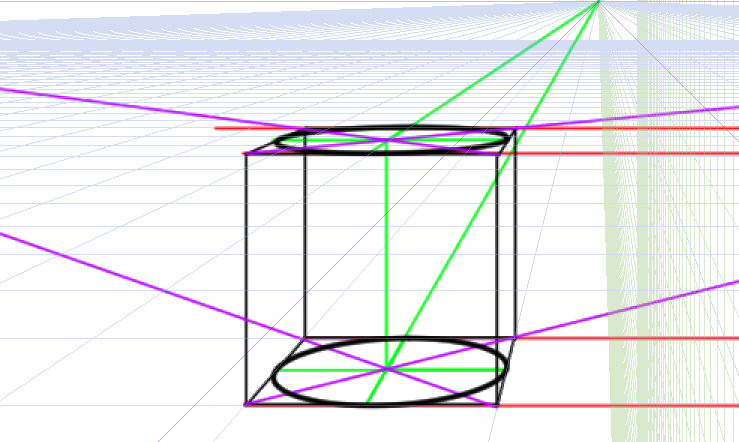
この位置に垂直な線を降ろしてみます。
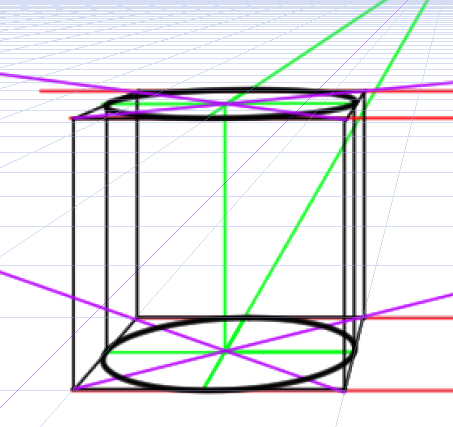
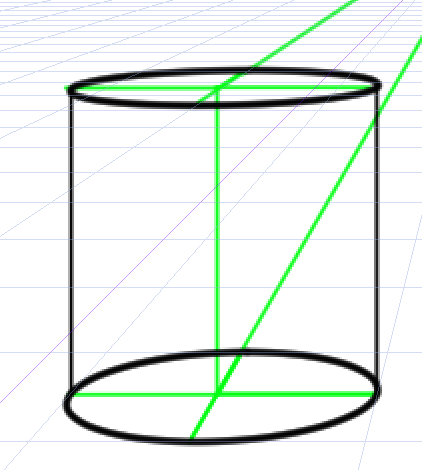
微妙に歪んだ円柱に見えてしまうことがわかります。これをもっと自然に見える円柱にするにはどうしたらいいのでしょうか。
『パース教室』(ロビー・リー)によれば、「短縮された円の実際の中心は、もとにした楕円の中心よりも、常に少し奥になる」そうです。
つまえり実際の中心は緑の線ですが、見かけ上はこの緑の線より少し前に垂直な線があるのです。同じ線の太さで比較してみます。
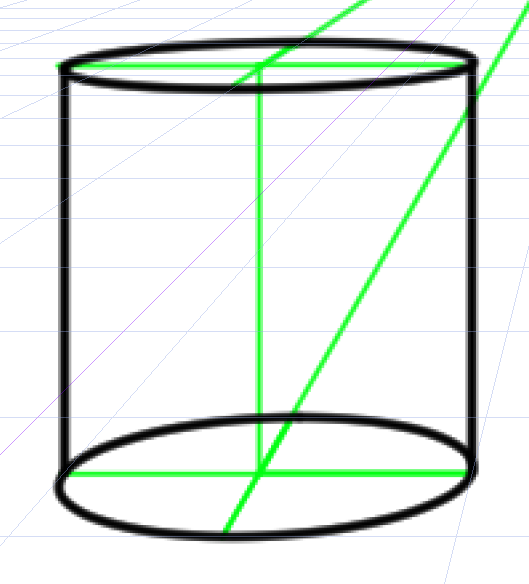
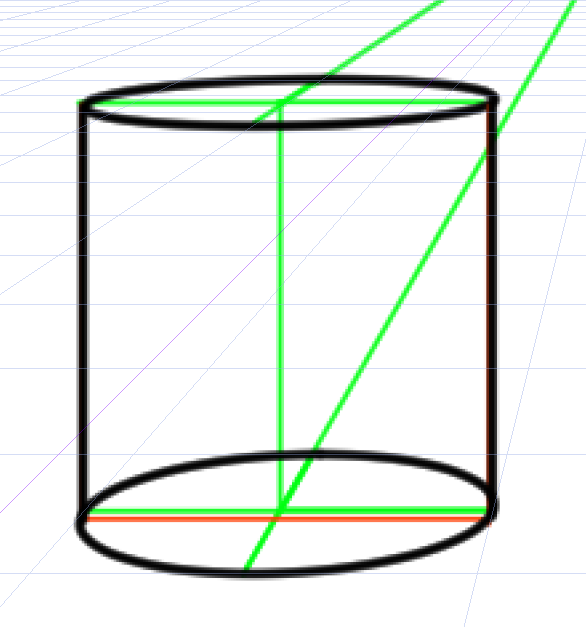
正方形の中心位置よりも少し手前のほうが自然に見える気がします。
これでいろんな大きさの円柱や楕円が描けるようになります。
すこし手前ということに厳密に拘る必要はないと思います。どれくらい手前にすればいいのかという数学的な話になってしまいます。自分が自然に見えると思う位置に線を引ければOKです。
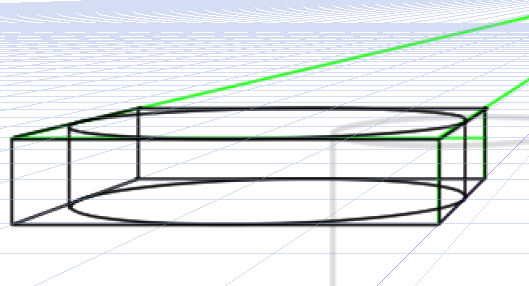

立方体で円柱を二点透視図法で作る方法について
これはかなりやっかいです。一点透視図法では幅と高さが等しいので簡単に高さがわかりました。二点透視図法では同じようにできません。

正方形を作ることはできますが、立方体を作るのは難しいです。高さがわからないからです。
この二点透視図法でつくった正方形に一点透視図法で作った正方形を加えるとうまくいくそうです。
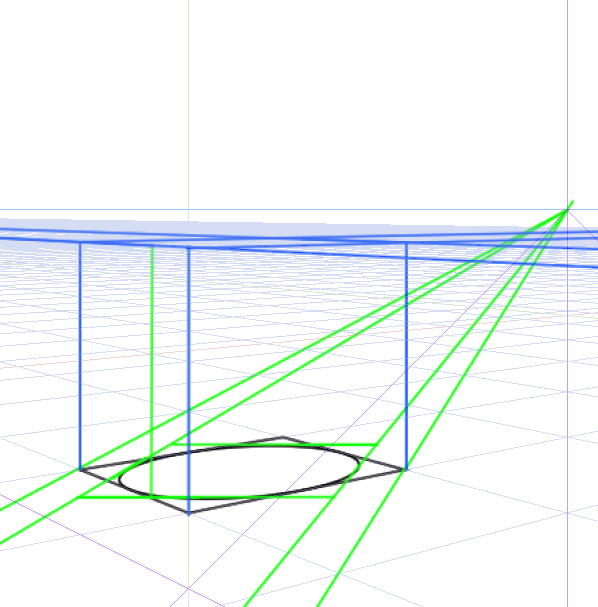
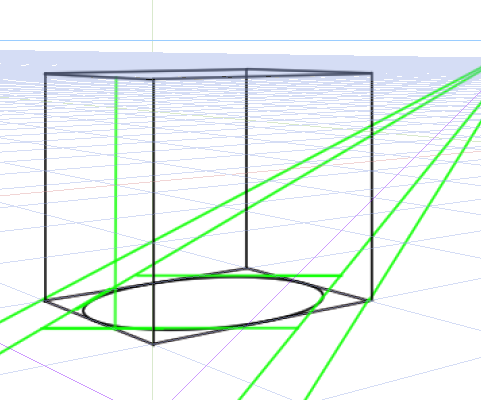
立方体ができたら同じように円柱を制作できます。
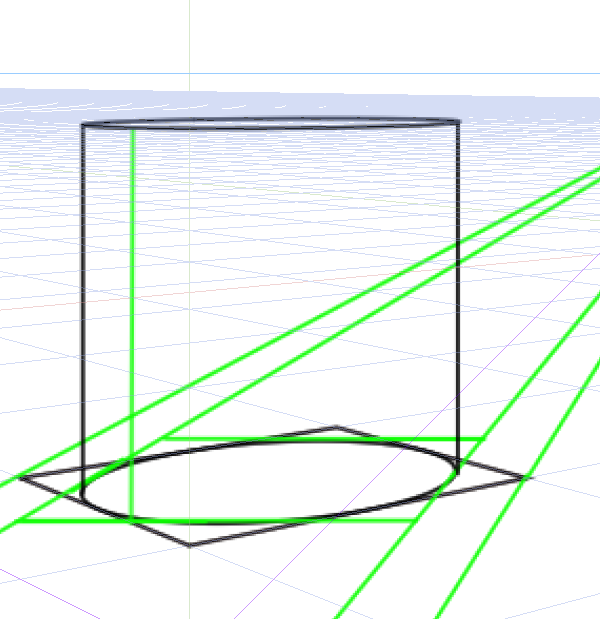
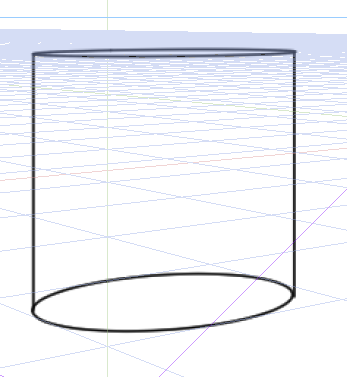
二点透視図法の円柱制作はかなりめんどくさいです。
デジタルなんですからもっと簡単にできてもいいはずです。グリッドとか上手く使えればいいのですが、どう使えばいいのか不明です。
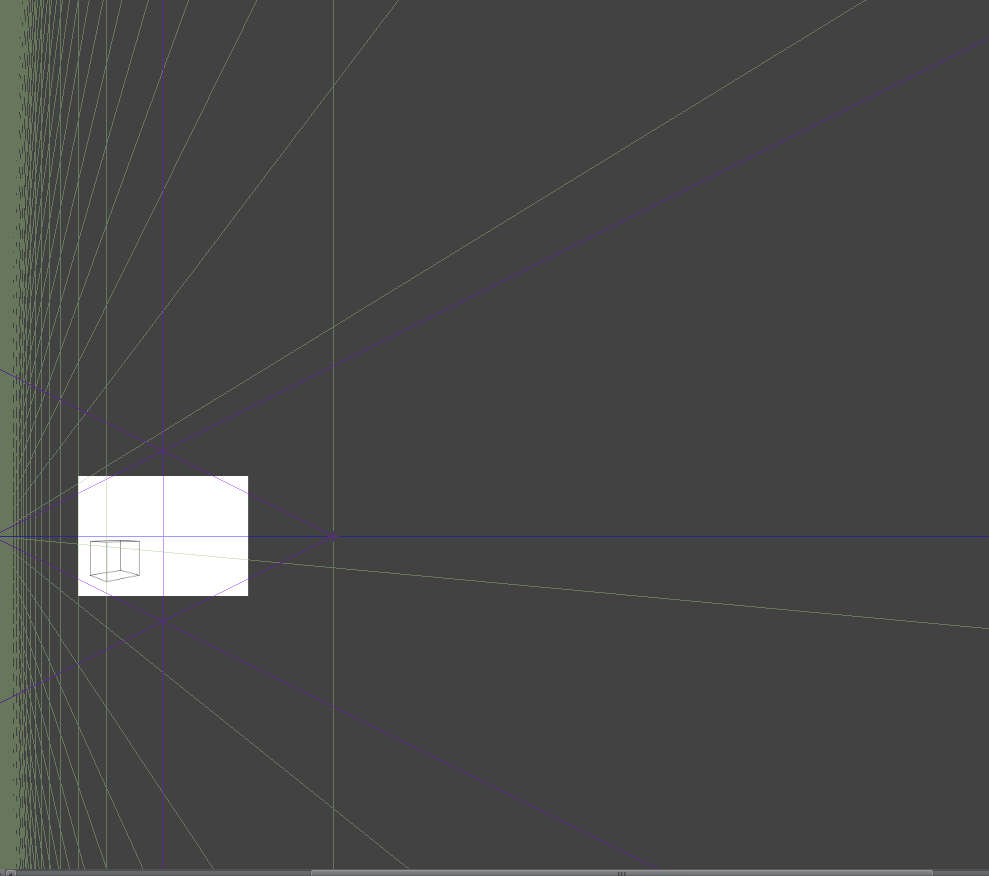
すこし解法を見つけた気がします。

グリッド線をなぞってみました。どういうことか最初から説明します。
まずは最初の正方形です。

これに二点透視図法のグリッドを表示します。
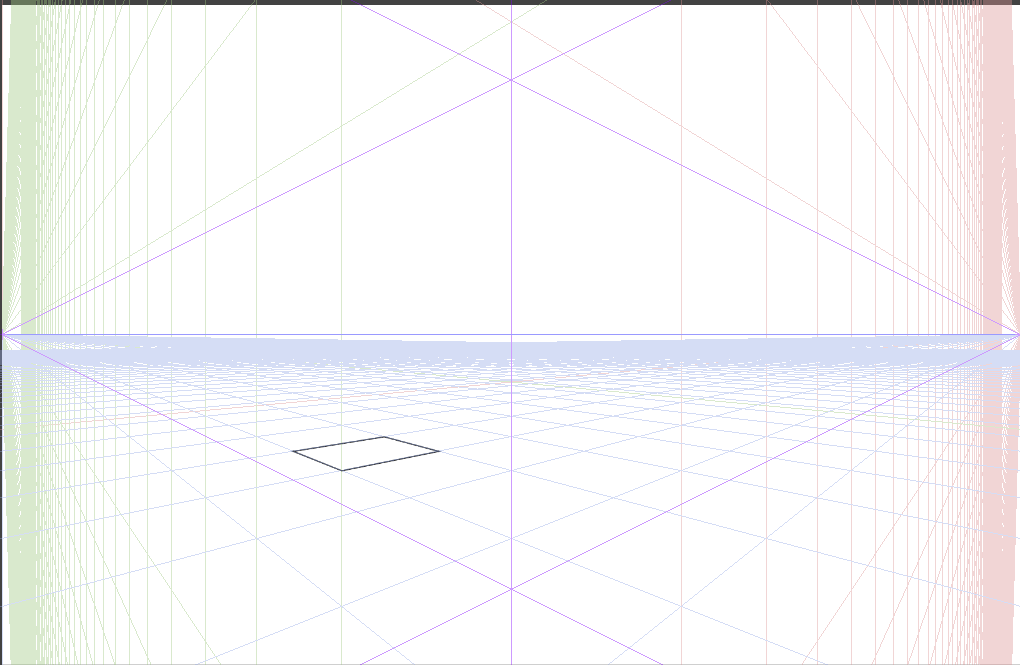
正方形の線を緑のグリッドまで伸ばします。交差している点に丸をつけました。
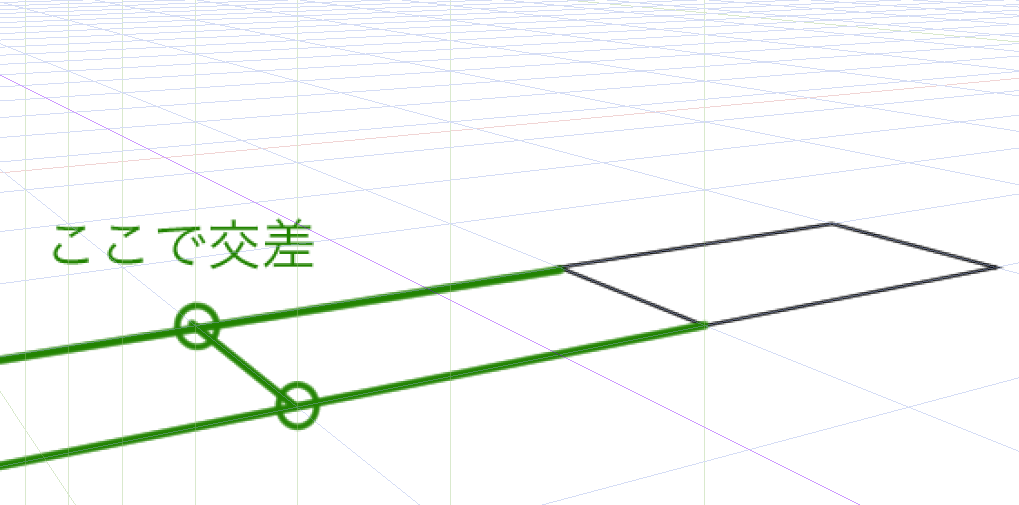
この線を基準に高さを決めます。
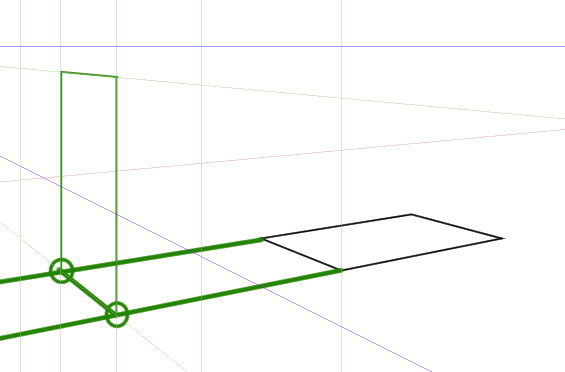
この基準線を最初に作った正方形へ伸ばしていきます。

基準線に従って作った高さを元にして立方体を形成します。

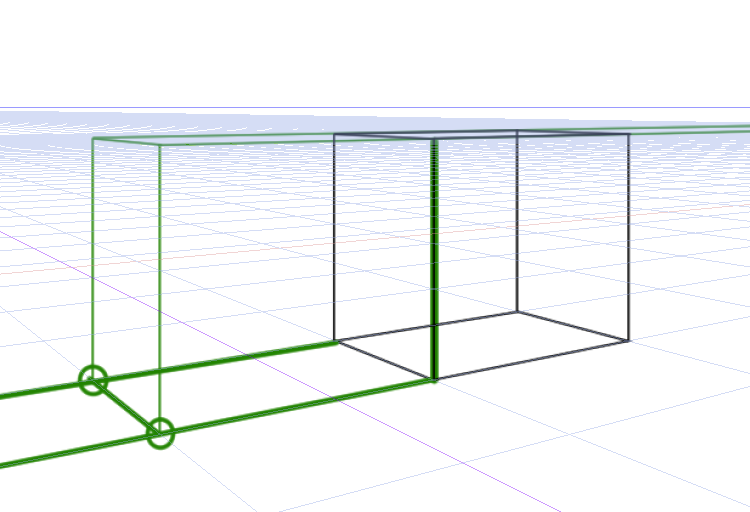
これできれいに立方体ができました。
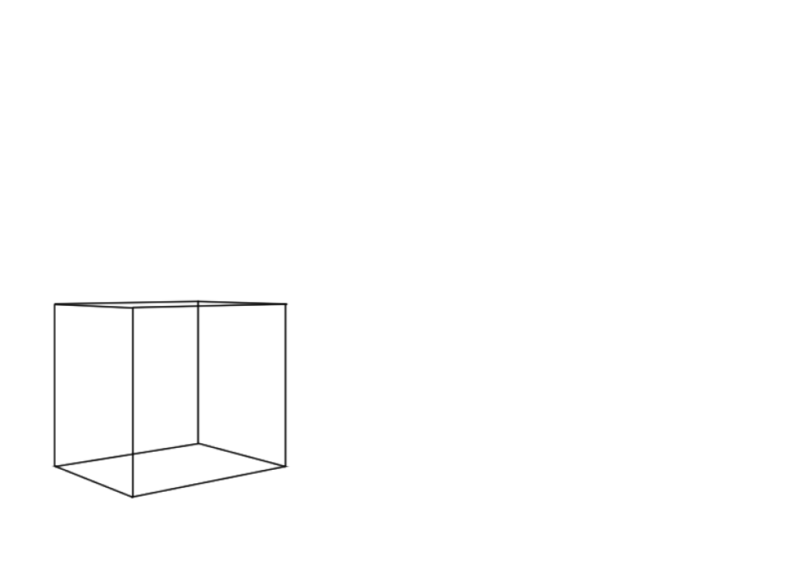
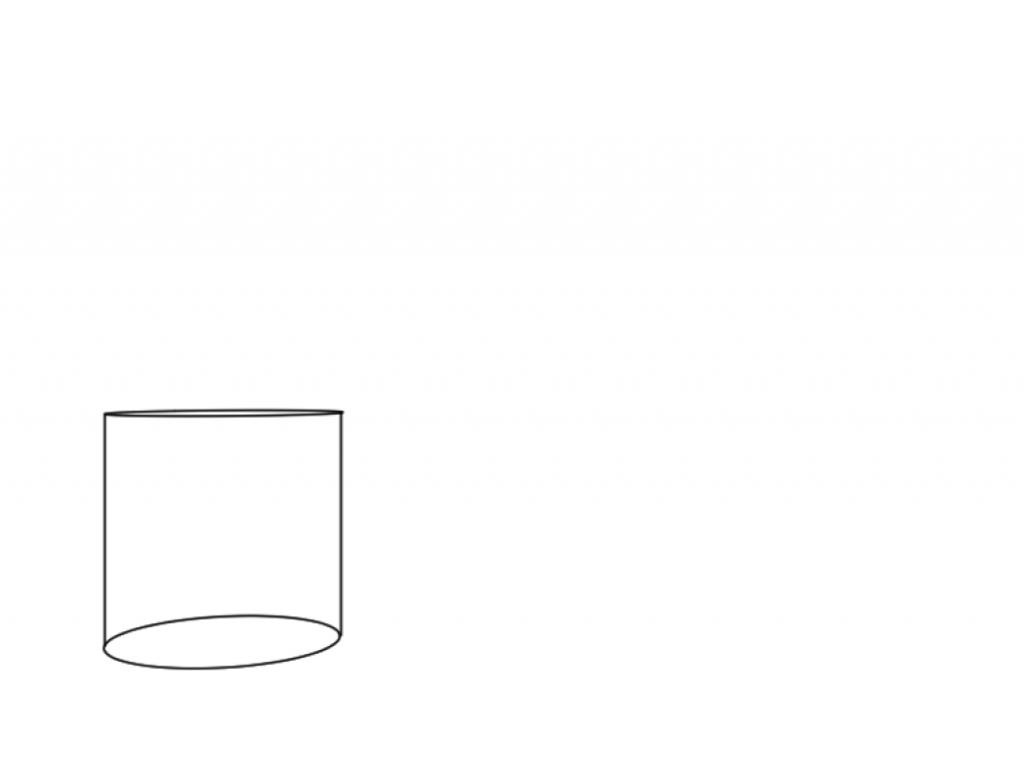
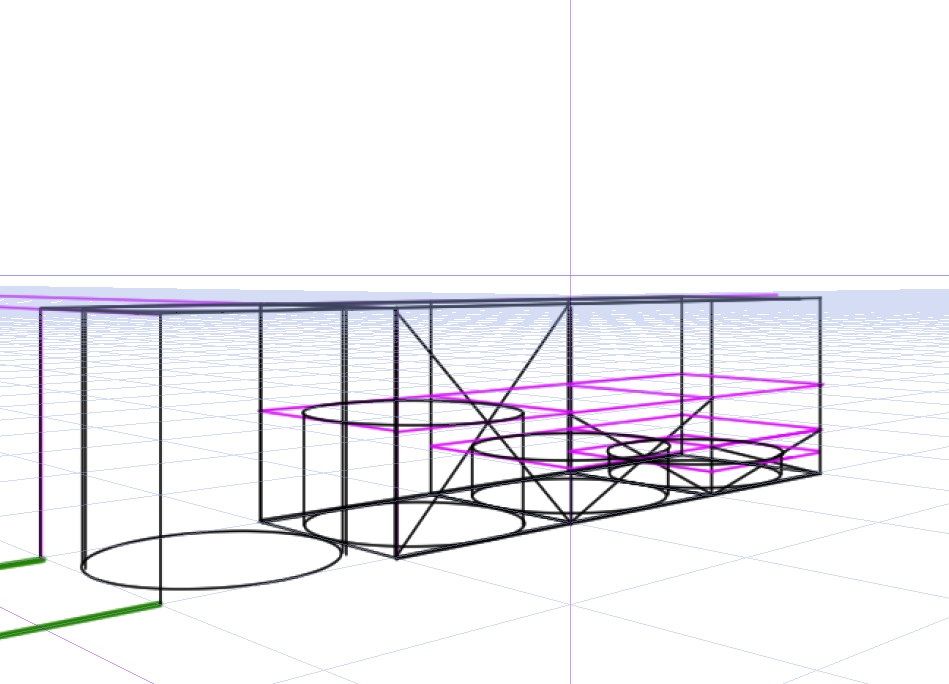
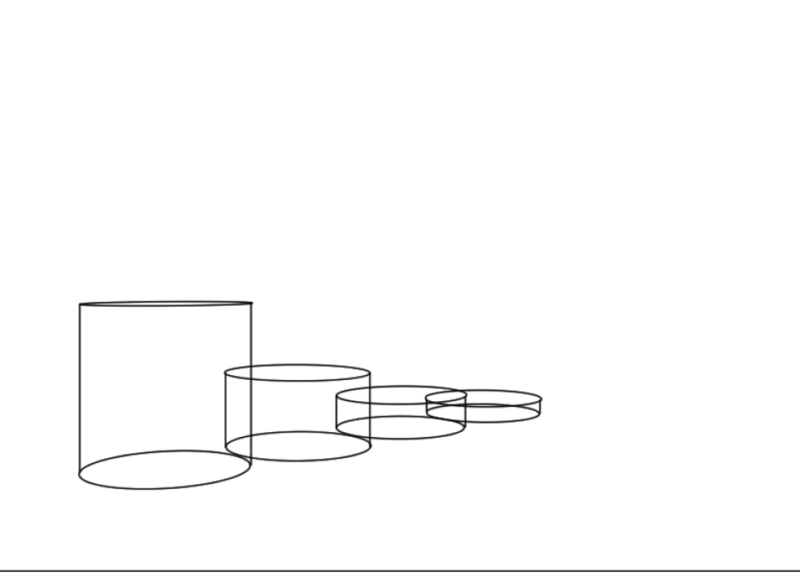
円柱も簡単にできます。もちろん分割もできます。
コメント
この記事へのトラックバックはありません。

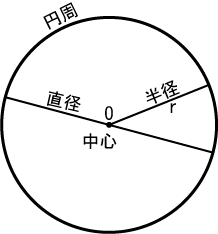 (wiki)
(wiki)









この記事へのコメントはありません。