視円錐とは何か
2024/10/17追記
この記事について、改善、修正したものを投稿しました。
【第三回】パースの基礎を学ぶ:一点透視図法で立方体を作成する方法、対角線の消失点について
【第四回】パースの基礎を学ぶ:パースにおける視円錐とはなにか、その設定方法
視円錐の定義
視円錐(COV,Cone of Vision)とは:画角を視覚的に表現したもの。視野の一部で、絵の中に実際に描き込むものを含む範囲(p,r,40,124P)。視心を中心とした一定範囲の視野を図形的に表現したもの(p,f)。線画によって示される視覚領域。周辺視野を除いた人間の標準的な視覚に関連する(h,s,202P)。
円錐(えんすい)とは一般にこのような形のものを指します(下図)。
画角を視覚的に、円錐で表したものが視円錐となります。
画角とは
画角とは:画角とは、写真や絵画で画として収まる範囲を角度で表現したもの(p,f)。画角(がかく、英: Angle of view)は、カメラで撮影される写真に写される光景の範囲を角度で表したものである。視野角とも(wiki)。
絵として収まる範囲を角度で表現したものが画角であり、それを目に見えるようにしたものが視円錐ということですね。
後ほど説明しますが、「画角とは立点と画面の両端を結んだときにできる角の角度(p,f)」のことです。
視円錐と人間の視野範囲について
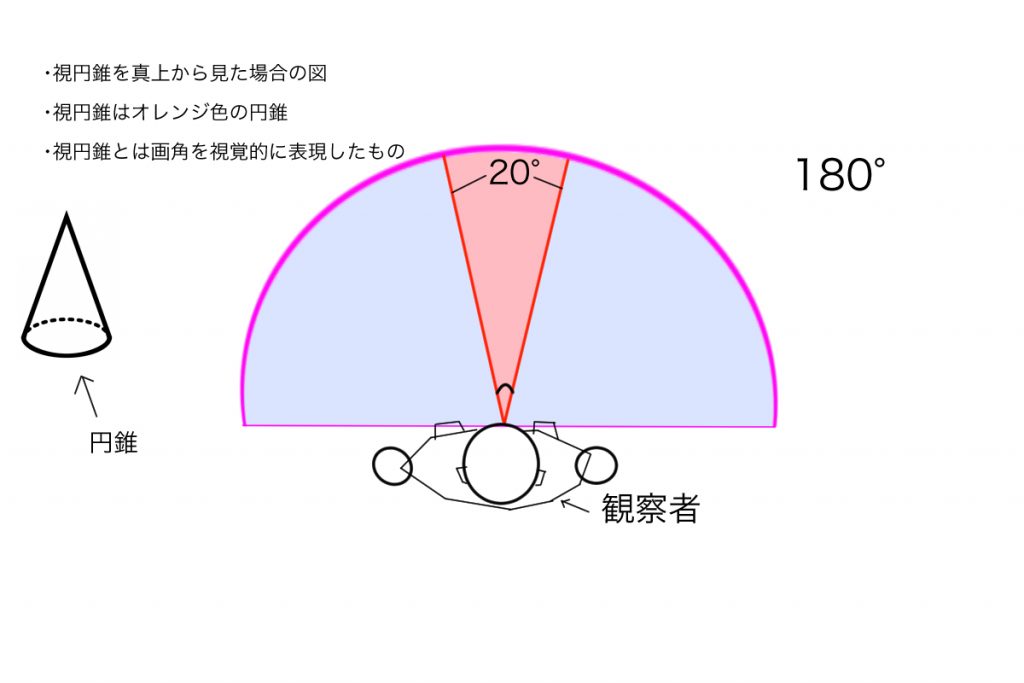
視円錐を目で見えるようにするとこのような円錐となります。人間の視野角は水平に200°、垂直に125°くらいらしいです。実際両目で見る場合は100°くらいです。100°でもかなり広いですよね。はっきりと物が見える範囲は45°~60°程度らしいです(p,f)。これは視円錐の角度が45°から60°が望ましい(あとで解説します)ことと密接に関係しています。
人間の視野範囲に合うような絵が望ましいということですね。もちろん芸術に決まりなどないので、時には斬新な視円錐を使うこともあるでしょう。しかし自然に見える角度というものはやはり人間の視野範囲に合うような角度だと思います。
あるオブジェクト(対象)をどのくらいの距離で見るかによって視円錐は変わります。対象に近づけば近づくほど視野は狭くなります。遠ざかると視野は広くなります。
このことはカメラをイメージするとわかりやすいです。たとえばカメラで目の前のパソコンを撮るとします。パソコンにカメラを近づけすぎると、パソコンのごく一部分しか撮ることができません。パソコンから距離を置けば、パソコン全体を撮ることができます。
すなわち対象との距離によって、画面に収まる範囲を調整できるということです。ちょうどいい距離はどこか、ちょうどいい画面はどのくらいの大きさかという問題は、ちょうどいい視野角は何度かという問題に密接につながっています。
視円錐、画面、ファインダーの関係
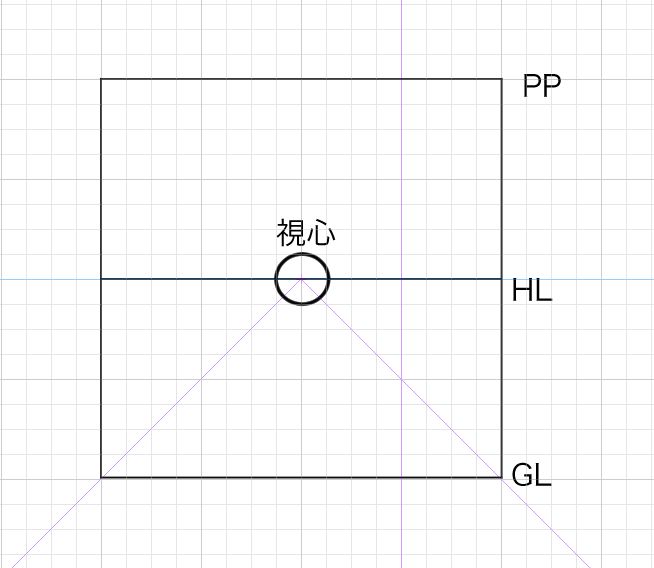
画面の定義
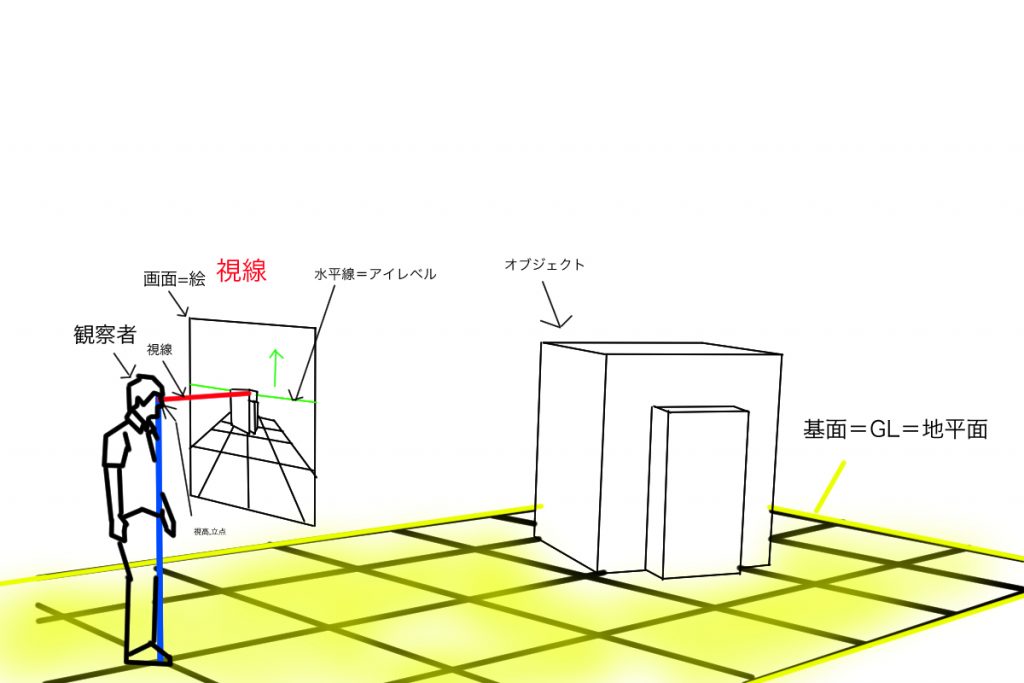
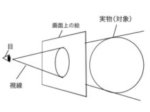
画面(PP,picture plane)とは:描いている視野を(たいていは)長方形に切り取ったもの。身の回り3次元の世界にカメラを向けた時、ファインダーに映る二次元の画像のようなもの(p,r,124P)。絵の一番手前に存在する平面で、そこに描線が描かれる。実際の画面と同一の広がりを持つが、空間に存在する別物。観察者と画像との視覚的な接触点(p,r,202P)。
画面とはこういいうやつです(下図)。PPと書いてあるのが画面です。よく「ガラス板」と言われたりします。
(g,y,21P)
ファインダーの定義
ファインダーとは:カメラにおいて目で構図を決めたりピントを合わせたりするのに使用する覗き窓及び液晶画面(wiki)
カメラのファインダーはこういうやつです
別にカメラじゃなくて手でもファインダーはつくれます。
画面と視野角の関係について
ファインダーとはいわば「視野を小さく切り取ったものを画面」なのです。絵を描く時も同じです。目に見えるものを全て、つまり視野全体を描いているわけじゃないです。見える視野の中で、ある一部分を絵にしているだけです。画面は視野の一部にすぎないのです。
また、視円錐は画面の幅と高さを決める役割を持っています。
このファインダーで視野を切り取るというのは大変面白いです。カメラって取る部分が丸いですよね。以下の画像をみればよくわかると思います(写真AC)。

しかし実際に撮れた写真は長方形ですよね。円形のレンズを、長方形の画面(ファインダー)で切り取るとはこういうことだと思います。
基線(GL)とはなにか、基面(GP)とはなにか
基線(GL,Ground Line)とは:基線=基面と画面が接する線。
基面(Groud Plane)とは対象物が置かれ、見る人が立っている面(g,y,20P)。基面=地平面。画面から水平線上へ向けて奥まっていく水平な理論上の平面(h,s,203P)。撮影者が立っていた、あるいは座っていた場所を地平面といいます(h,s,22P)。
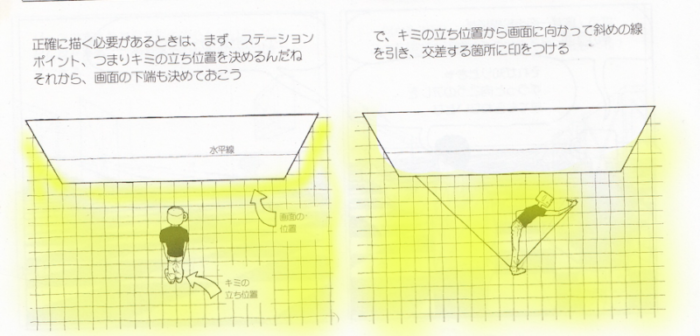
(p,s,21P)
画面(PP)におけるGP(基面)と接する線がGL(基線)です。
なぜ基面(GL)を理解する必要があるのか
次の項で扱う「画角と画面の関係」を理解するためにはGLの理解が不可欠だからです。画角とは視円錐の角度をここでは意味します。そして画角はSP(立点)とPPの両端を結んだときにできる角度をさします。
また、GLの理解は「対角線の消失点」を理解するためにも重要です。なぜなら対角線の消失点は立点からPPのGLへ向かう線の延長上にあるからです。

(p,d,82-83P)
マグ本のページで言うとおそらくこのあたりがGLだと思います。

すこし傾いててすいません。このように、立点から、GLへ、GLからHLへという順に対角線の消失点は決まります。
画角と画面の関係
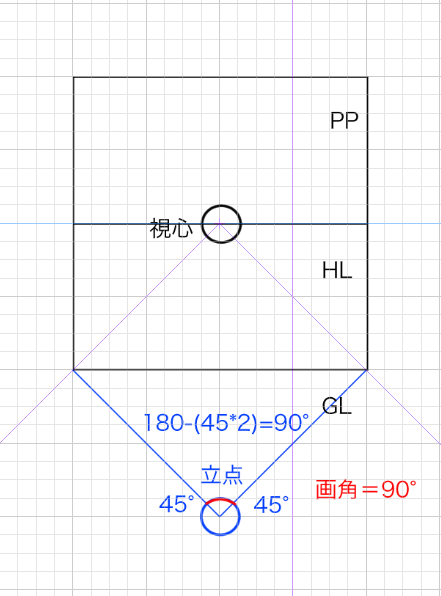
画角と画面の関係とは:画角とは立点(SP)とPPのの両端を結んだときにできる角の角度(p,f)
これを絵で理解してみたいと思います。まずは45度の視円錐を想定します。45度の視円錐をつくるためにまずは画面を作ってみたいと思います。
画角とはSPとPPの両端を結んだときにできる角度でした。仮に90°の画角だとすれば、画面の両端からちょうど斜めに線を引いた位置に立点があるはずです。仮に100°視野が見渡せるとして、画面で90°に切り取るのです。
もし45度の画角にしたい場合はどうすればいいでしょうか。そうです。もっとSPをPPから離せばいいのです。
どのくらいかというと、90度のおけるPPからSPの距離を2倍にすればいいのです。画面の高さ分、距離を置きます。これも後で説明しますが、対角線の消失点は45度の位置にできます。立点を遠ざければ、その分対角線の消失点も遠ざかります。実際に描いてみます。
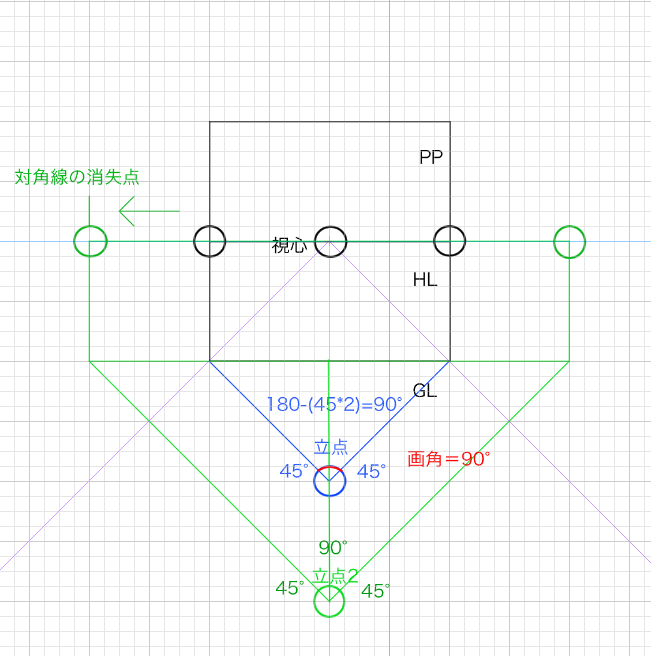
これじゃ視円錐の画角は90°のままじゃないかと思うかもしれません。しかし画角とは立点(SP)とPPのの両端を結んだときにできる角の角度でした。したがってPPから新たな立点2へと線を伸ばしてみれば画角は45°であることがわかります。念のため分度器でも測ってみましたが画角は45°でした。
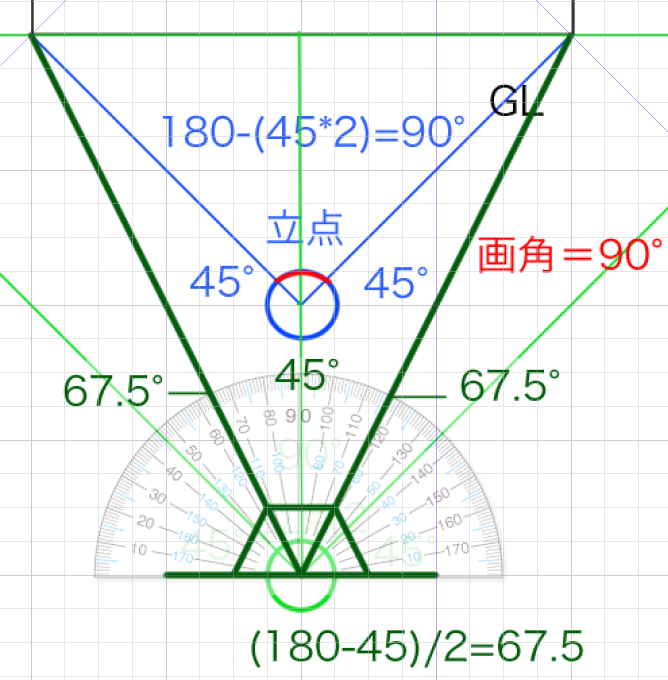
これを視円錐にしてみます。まずは”画面における”90度の視円錐からです。これは立点1から画面を見ていた場合の視円錐です。
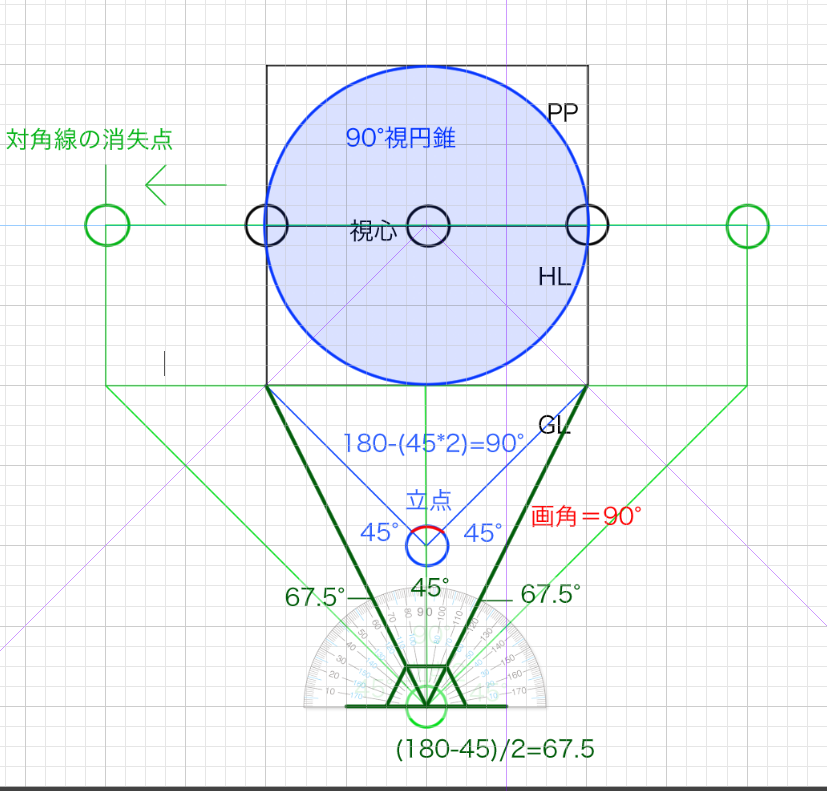
次に2つめの”画面外”における90°視円錐です。これは立点2から画面を見ていた場合の視円錐です。

そしてこれが”画面内”における45°視円錐です。これは立点2から画面を見ていた場合の視円錐です。
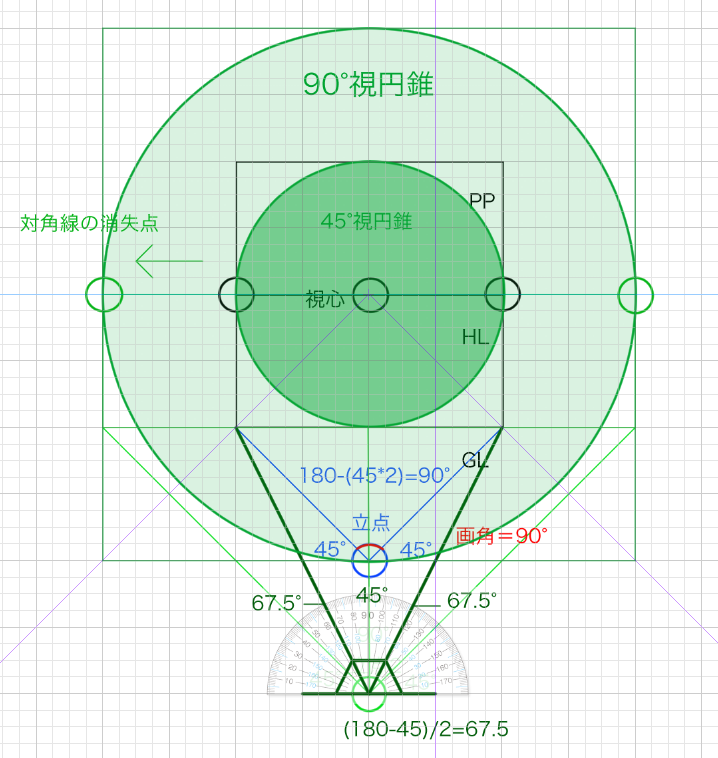
改めて見ると、立点1からの90°視円錐と立点2からの45°の視円錐のお起きは変わりません。ですが、立点1からの対角線の消失点位置と、立点2からの対角線の消失点位置は異なります。対角線の消失点は立点から45度の位置にあります。つまりちょうど視円錐90°ができる位置にあるということです。
視円錐の大きさは同じですが、対角線の消失点の位置が違うということはかなり重要です。実際に絵で対角線の消失点位置の違いを見てみます。
まずは立点1における視円錐90°の対角線の消失点位置からです。対角線の消失点は「画面内」にあることがわかります。
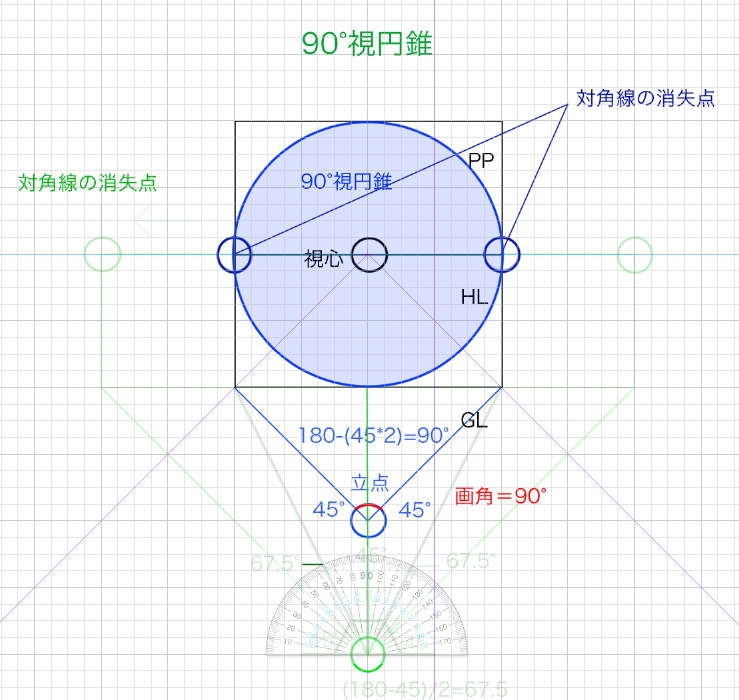
次は立点2から見た対角線の消失点です。「画面外」にあることがわかります。

そして立点2から画面内にある45度の視円錐はこちらです。すこし無駄なものを省いて整理しました。立点1からの視円錐90°と視円錐の見た目の大きさは同じですが、立点2からの視円錐45°の対角線の消失点は異なることがわかります。

ちなみに立点1から視円錐45°をつくるとおそらくこうなります。
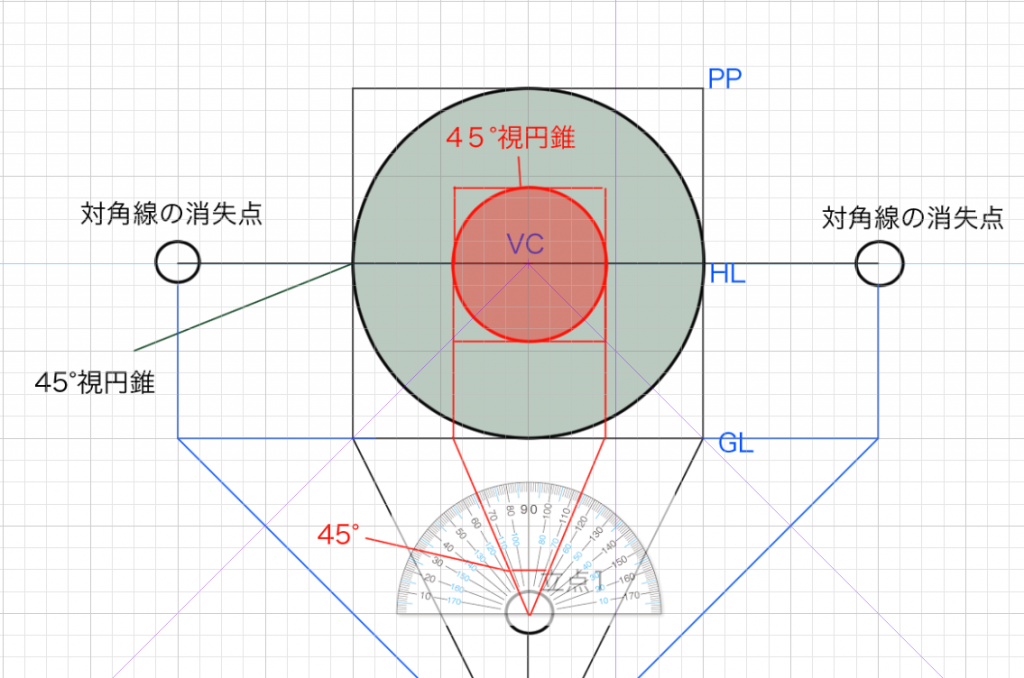
視円錐・対角線の消失点を通して立方体の作成を考える
立方体とはなにか
立方体とは:直方体のうちで、すべての面が正方形のもの。正六面体ともいう(日本大百科全書)
(wiki-正六面体)-立方体
対角線の消失点っていつ使うの?って思ってました。よくよく読んでみると「立方体」を描くときに便利みたいです。文系というのは言い訳にできないほど、立方体は常識的な基礎知識ですね(すっかり忘れてました)。立方体というのはすべての面が正方形のものらしいです。正六面体というそうです。
立方体と直方体の理解はした方がいいかもしれません。たとえば直方体は、立方体であるとは限りません。なぜならすべての面が正方形ではないものも直方体にあるからです。ちなみに直方体とはすべての面が長方形で構成される六面体です。正方形も長方形の一種だそうです(困惑)。
(wiki-直方体)
対角線の消失点とはなにか
対角線の定義:長方形や正方形の向かい合う2つの角を結んだ線。一般的には、2つの隣り合わない点を結んだ線も指す(p,r,124P)。
対角線の消失点(DVP)の定義:正方形を描くためにb使う消失点。短縮された長方形に、角を二等分する対角線を引くために設定する。この短縮された長方形は「正方形」になる(p,r,124P)。
そもそも透視図法における「対角線の消失点」ってなに?
マグ本における対角線の消失点の説明を紹介します。
マグ「でも、デウィッド、対角線がたどり着く消失点はどうやって決めればいいんだよ?」
デウィッド「それは、キミと画面の距離によるね(p,d,82P)」
マグが言っている「対角線がたどり着く消失点」とはここでいう「対角線の消失点」です。ポイントを少しまとめます。
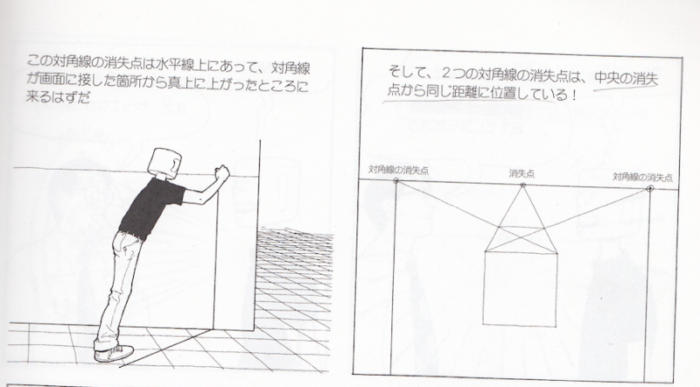
・対角線の消失点は観察者と画面の距離で決まります。
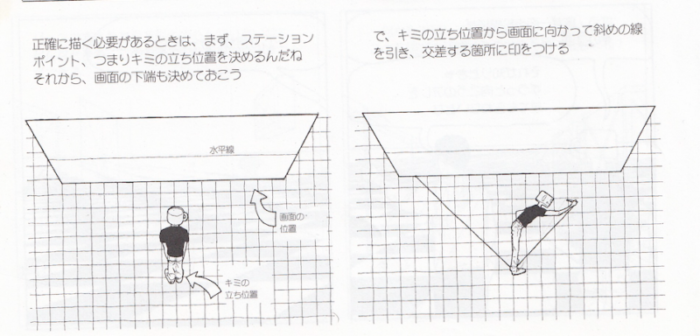
・正確に描く場合はステーションポイント(立点)を決める必要があります。
・対角線の消失点は水平線上にあります。
・2つの対角線の消失点は中央の消失点(視心)から同じ距離に位置しています。
・画面に近いところに立っていたら対角線の消失点は互いに近づきます。遠いところだと離れます。
立方体を描いてみる(一点透視図法+二点透視図法)
今回は先程学んだ視円錐45°を使って対角線の消失点を作り、立方体を作成してみます。詳細は前項の「画角と画面の関係」を参照してください。
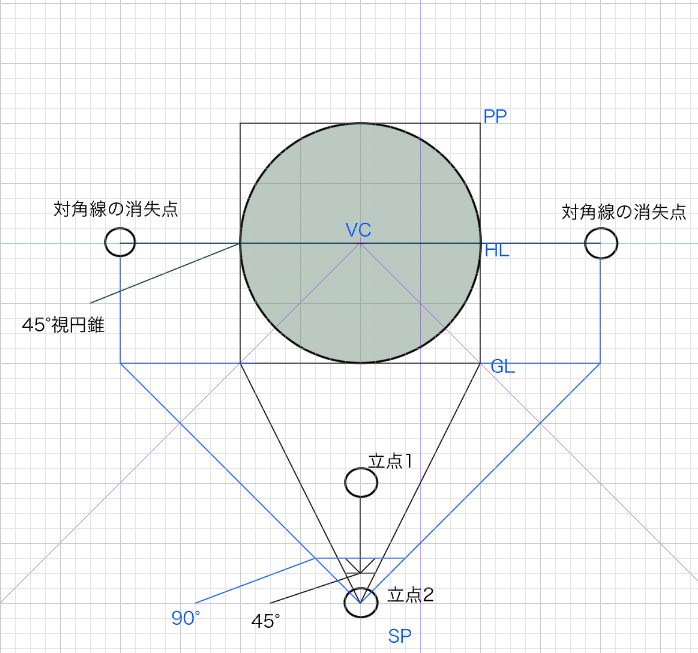
さてここから画面に立方体をたくさん作っていきます。試しに縦マス、横4マスの立方体を作ります。

次に一点透視図法なのでVCへ向かって線を引いていきます。VCとは視心です。

次に対角線の消失点へ向けて線を引きます。

VC(視心)へ向かう線と、対角線の消失点(DVP)へ向かう線を利用して立方体を作成します。
この方法では対角線に二点透視図法が使われているというのがポイントです。
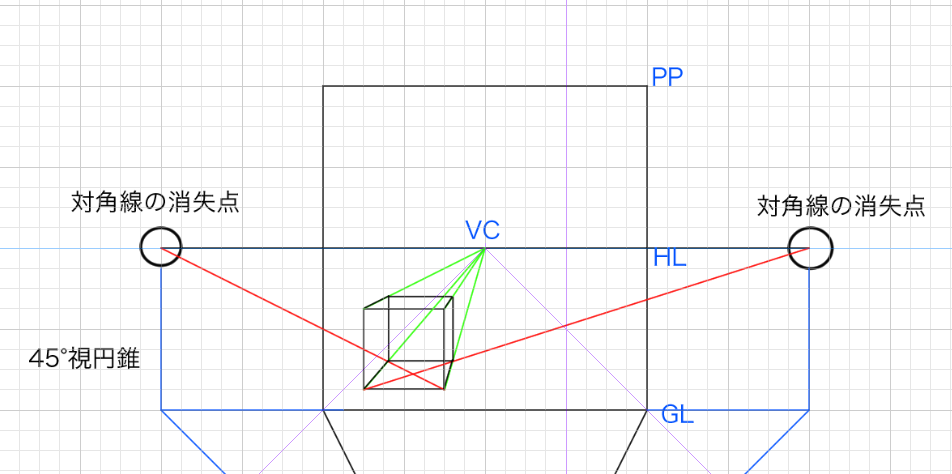
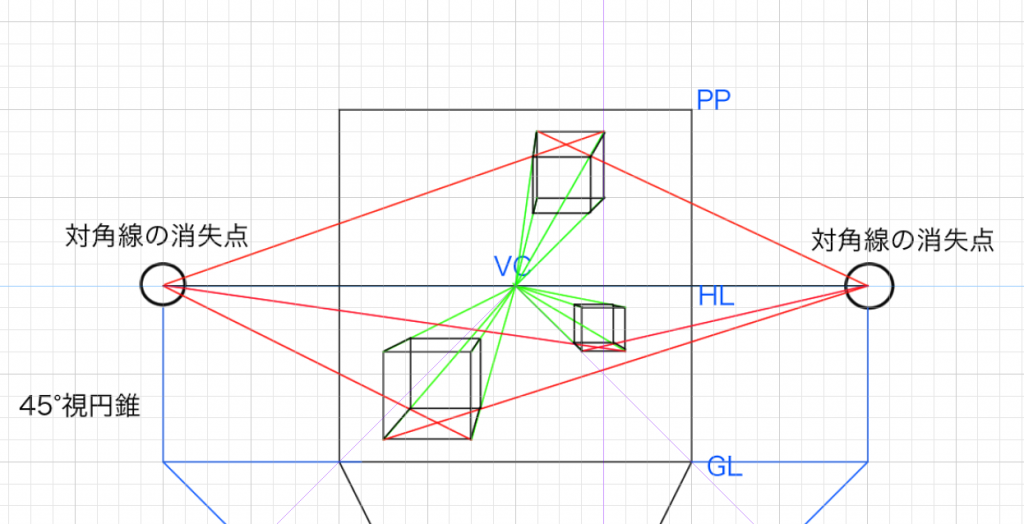
これで立方体の完成です。どの大きさでも好きな位置に置くことができます。
立方体を描いてみる(簡略版)
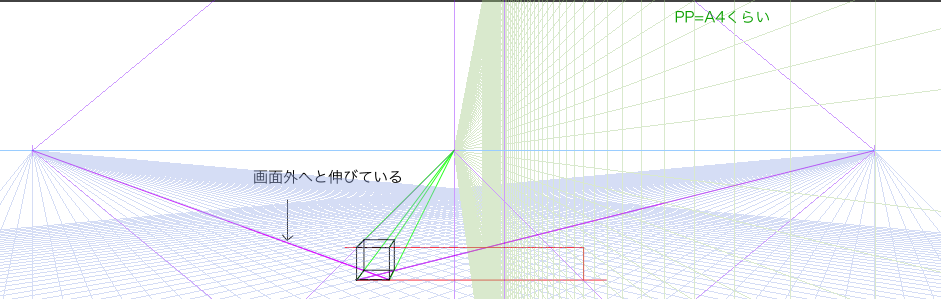
いちいち立点を決めたりするのがめんどくさいと思います。そこで、画面の横幅の1/2の長さに対角線の消失点を適当に設置し、画面外に90度の視円錐を作り、画面内では45度の視円錐を作ってみます。画面はA4とします。

デジタルの場合はキャンバスサイズを大きくして、画面外に対角線の消失点を設置します。アナログの場合は同じような大きさの紙を両端に用意してもいいかもしれません。
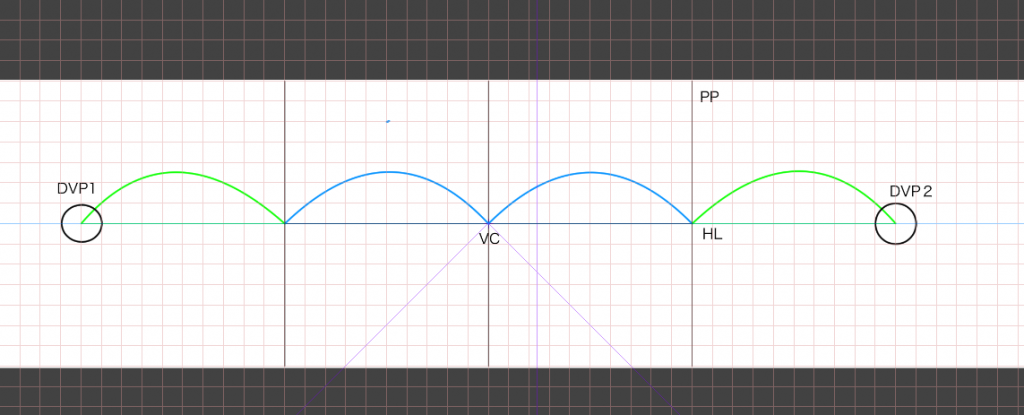
あとは先程と同じように立方体を作っていくだけです。
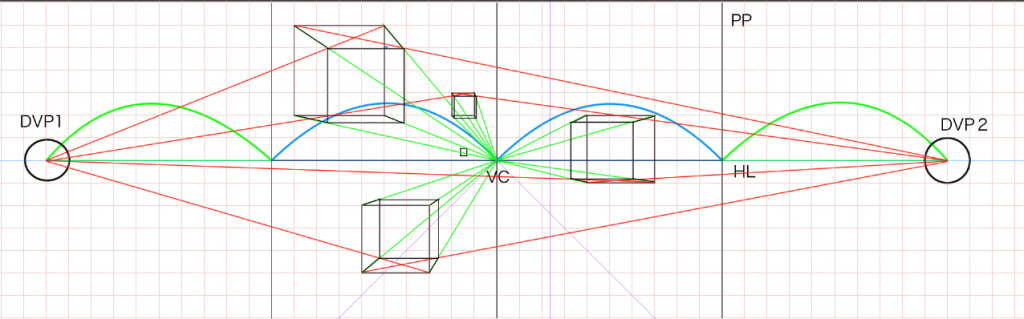
補助線レイヤーを作っておけばきれいに消せます。描き終わったらキャンバスサイズを戻してもいいですし、トリミングしてもOKです。

今思ったのですが、キャンパスサイズの端に対角線の消失点が来ることを利用して絵を描けばいいんじゃないかと思います。

これが初期位置の一点透視図法と二点透視図法の消失点です。
画面の端に来ています。
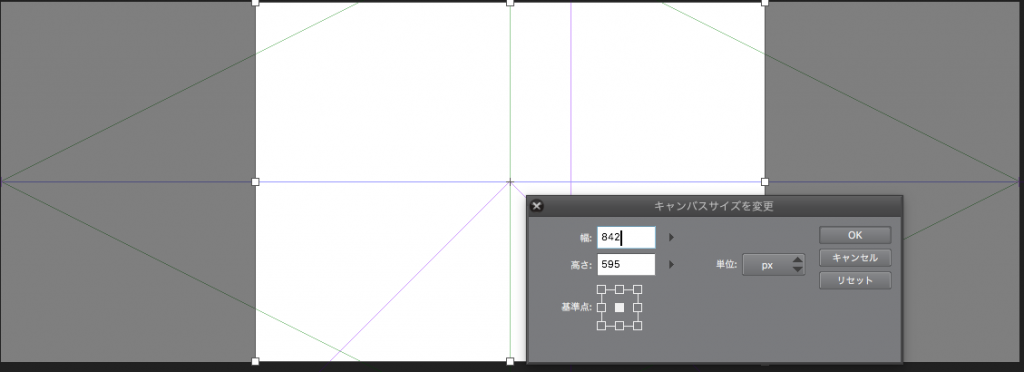
幅が842ピクセルです。対角線の消失点を中央から数えて842ピクセルが好ましいです。つまり、842/2で421ピクセル先に対角線の消失点があればいいのです。
ということは最初から横幅を842の2倍、つまり1684ピクセルで設定したらいいのではと思います。
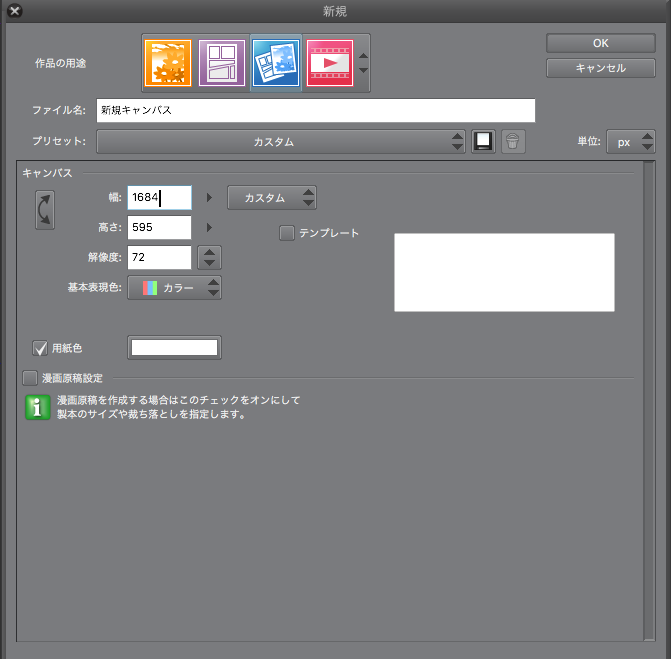
これで設定すると以下のようになります。
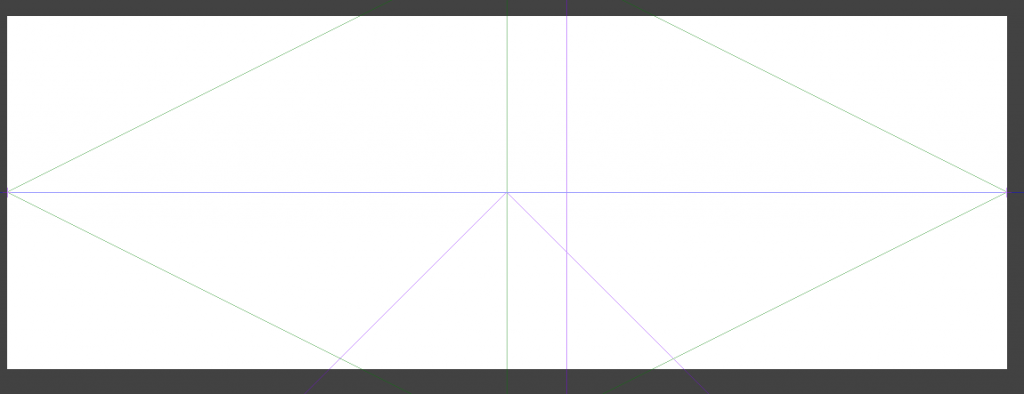
そしてキャンパスサイズの幅を842に戻せばいいのです。そうすると画面外に消失点を設定できます。
グリッドが一致して便利ですね。

視円錐は何度が最適か
一点透視図法における視円錐のベストな角度
一点透視図法におけるベストな視円錐の角度:視円錐は40°-50°(h,s,23P)
一点透視図法は歪みがきつくなる傾向があるみたいです。歪みのきつさを抑えるためには、視円錐は50°から40°にしたほうがいいですね。視円錐をせばめすぎると、望遠レンズで撮影したみたいに不自然になってしまうそうです(h,s,22P)。
二点透視図法における視円錐のベストな角度
二点透視図法におけるベストな視円錐の角度:視円錐は60°以内(h,s,23P)
大半の透視図は60°の視円錐で書かれているそうです(h,s,22P)。一点透視図法より広い視円錐を使えます。
三点透視図法における視円錐のベストな角度
三点透視図法におけるベストな視円錐の角度:視円錐は60°以内(h,s,23P)
二点透視図法と同じく60°以内に収めたほうがいいみたいです。
クリップスタジオペイントでパースレイヤーを使って立方体をつくる(主に一点透視図法)
クリップスタジオペイントの一点透視図法の使い方:パースレイヤーを使う
まずはクリップスタジオの上の方にある「レイヤー」から「定規・コマ枠」を選択し、「パース定規の作成」を選択します。
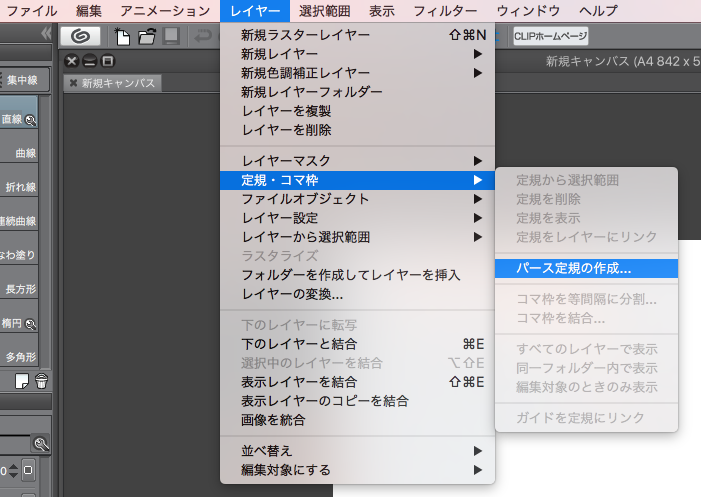
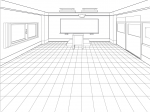
そうするとこのような画面が出るのでOKを押します。

このようパースな画面になります。

次にツールプロパティ[オブジェクト]を選択してグリッド線を加えてみます。
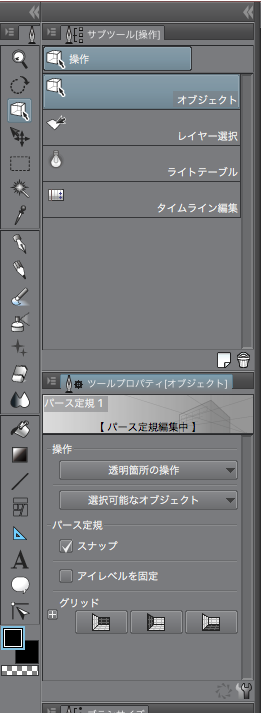
グリッドのところを全てクリックするとこのようになります。状況によって一部を表示したりして活用します。+を押せばグリッドサイズも調整できます。


さてこれでパース定規の準備は完成しました。
クリップスタジオペイントの一点透視図法の使い方:立方体を作成してみる
これまでの記事で学んだことをパース定規を使って実践するだけです。たとえばグリッドサイズ10の、40*40の立方体を設置してみます。まずは正方形をマス目にそって描きます。
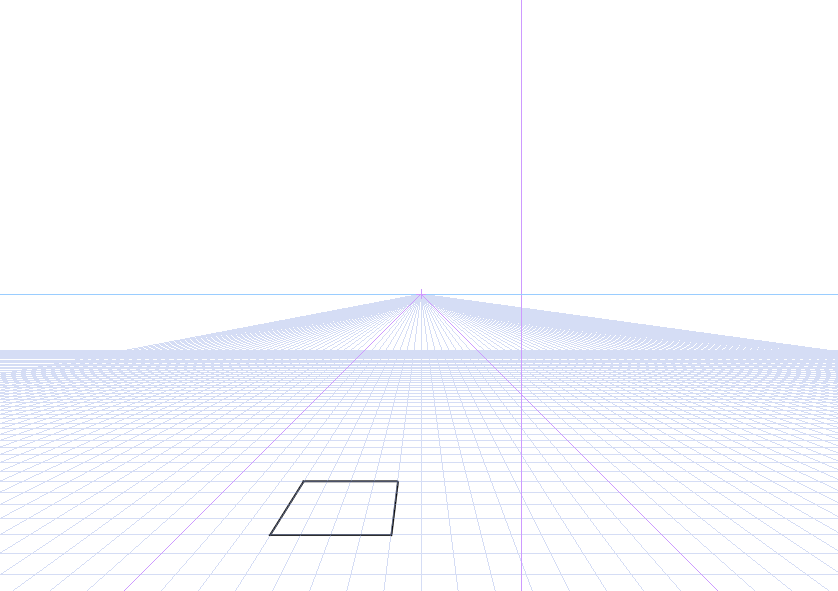
ここから縦の長さをグリッドで調べます。立方体なので縦のグリッドも4マス分とります。
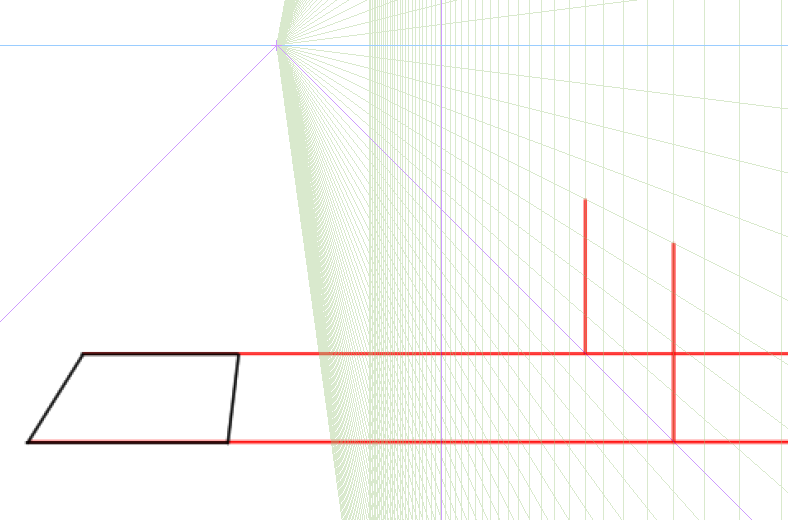
あとはそれにそって立方体をつくれば完成です。
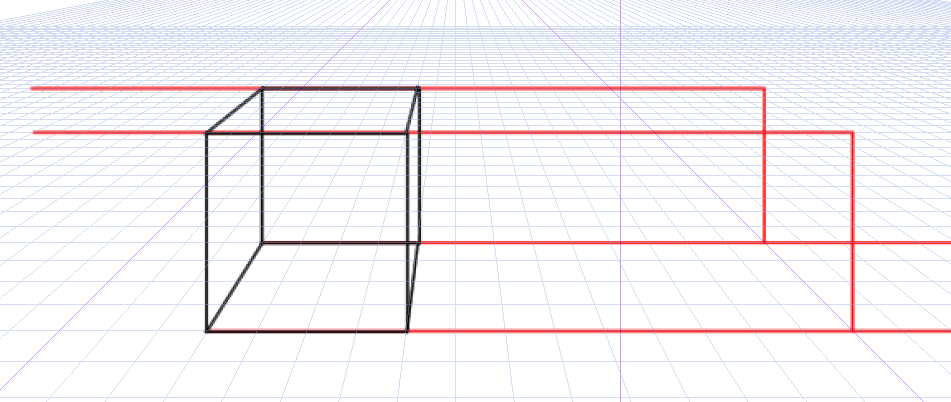
同じ方法で分割もできますし、複製も可能です。さざまな大きさの立方体を作ることができます。

クリップスタジオペイントの一点透視図法の使い方:視円錐何度なの?(ただの考察です)
パースを自動的に設定してくれるのはありがたいのですが、何度なのかよくわかりません。調べてみます。
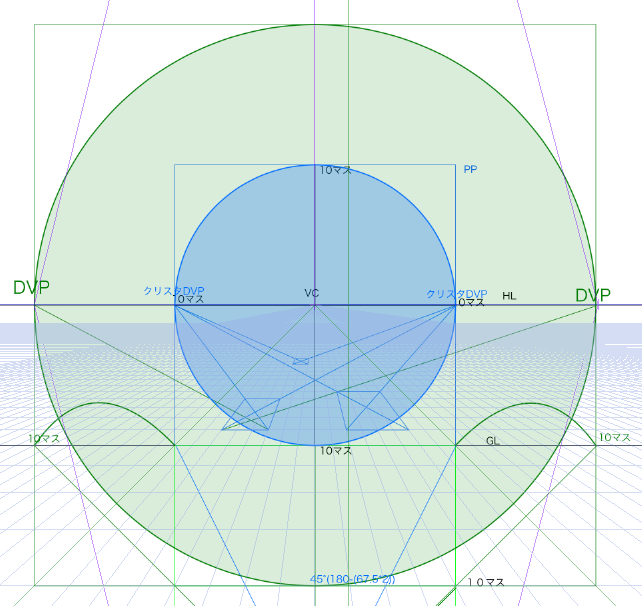
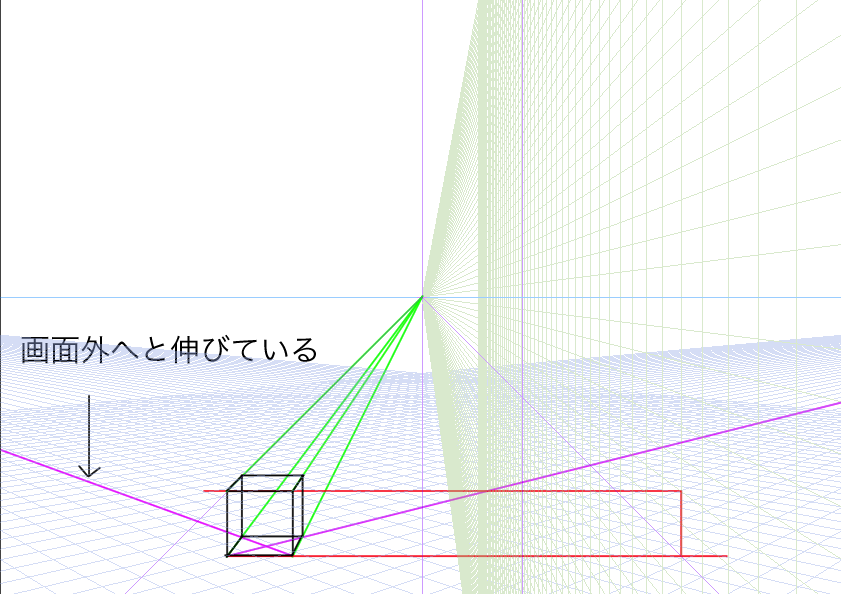
最初の画面サイズを正方形サイズにして、立点を設定し、90度の視円錐を画面外に作り、かつ45度の視円錐が画面内にくるようにしてみます。
正方形の画面を元にして作成するとおよそこのような形になります。説明すると青い線で囲まれたPPが画面です。縦20マス、横20マスとなります。そしてSPは立点です。詳しいことはすでに説明したので参照してください。視円錐の画角はSPとPPの両端を結んだときにできる角度でした。SPからPPの端(GL)に向かって線を45°引けば視円錐の画角は90°になります。なぜなら180°-(45*2)=90°になるからです。
この90度の位置でできる点は対角線の消失点(DVP)となります。もちろん立点の位置によってDVPの位置は変化します。一点透視図法においては画面外にDVPをおいたほうが自然に見えます。
そして画面内にはちょうど45°の視円錐ができます。
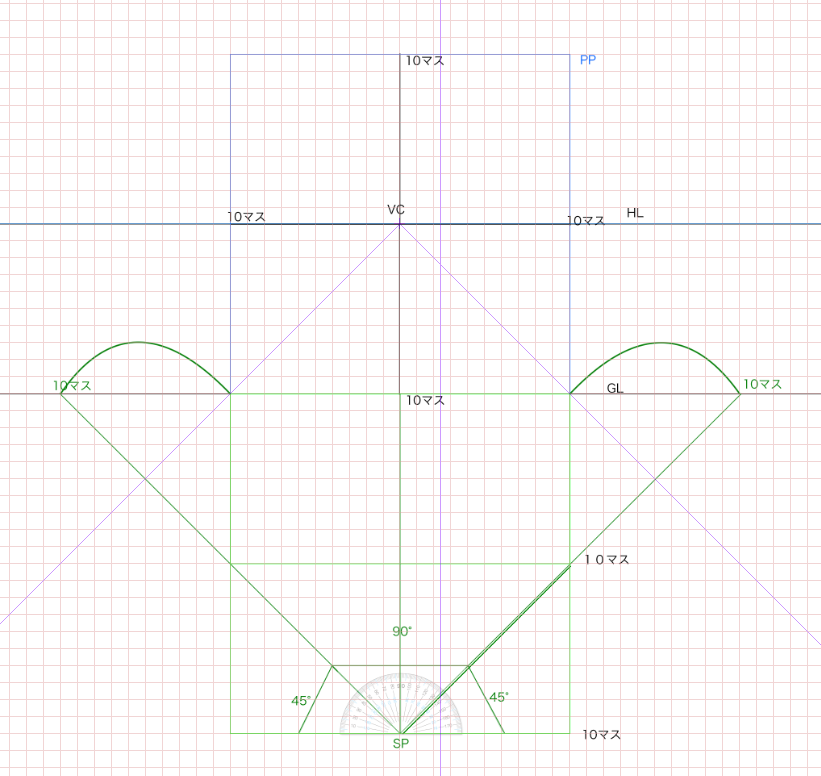
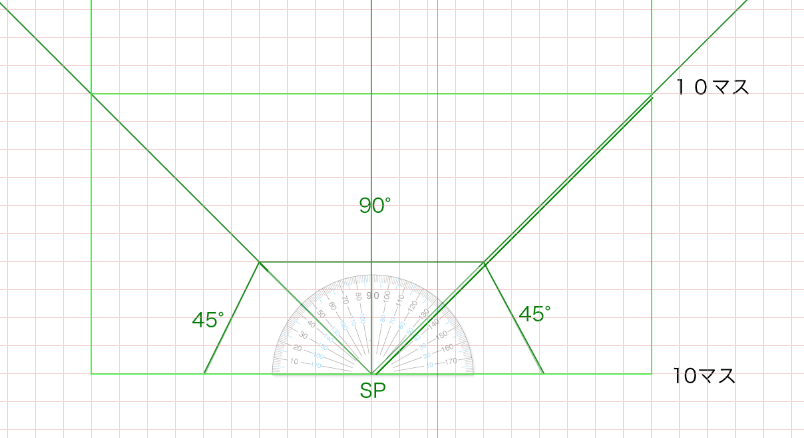
SPから45度の線をGLへ向けて、そのGLから垂直にHLへ線を伸ばした位置が対角線の消失点(DVP)です。90°視円錐を塗るとしたらおそらくこのような感じです。
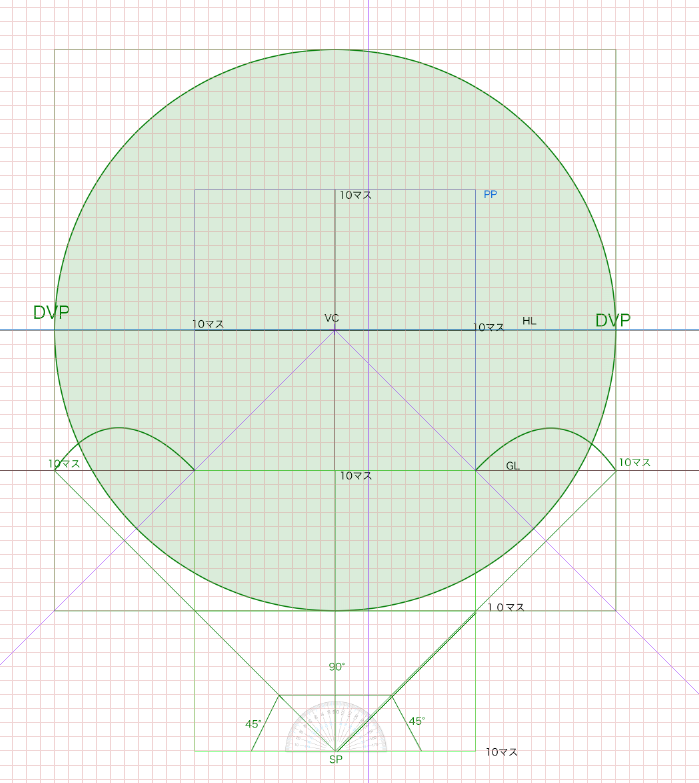
そしてSPから視円錐が45度になるようにさらに線を引きます。
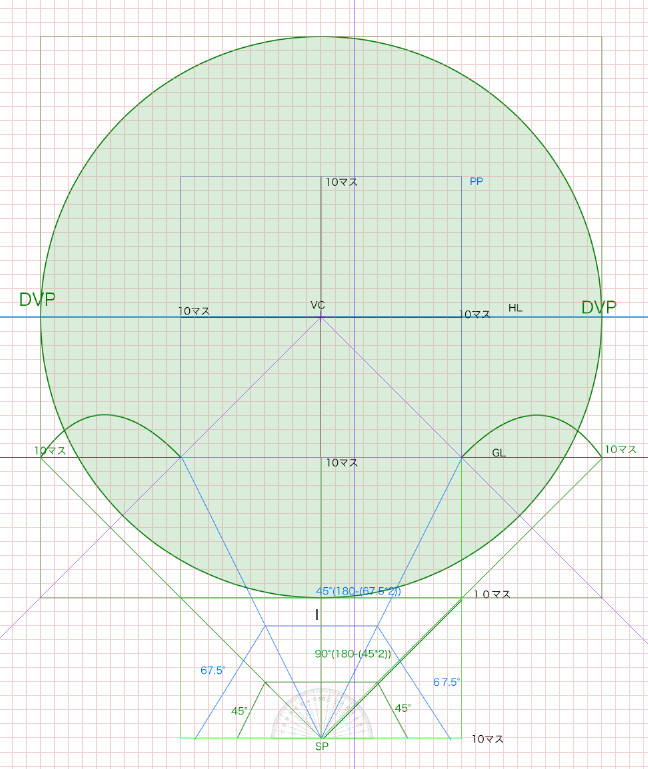
ついでに45度の視円錐も青で塗りつぶしてみます。ちょうど画面内にくることがわかります。
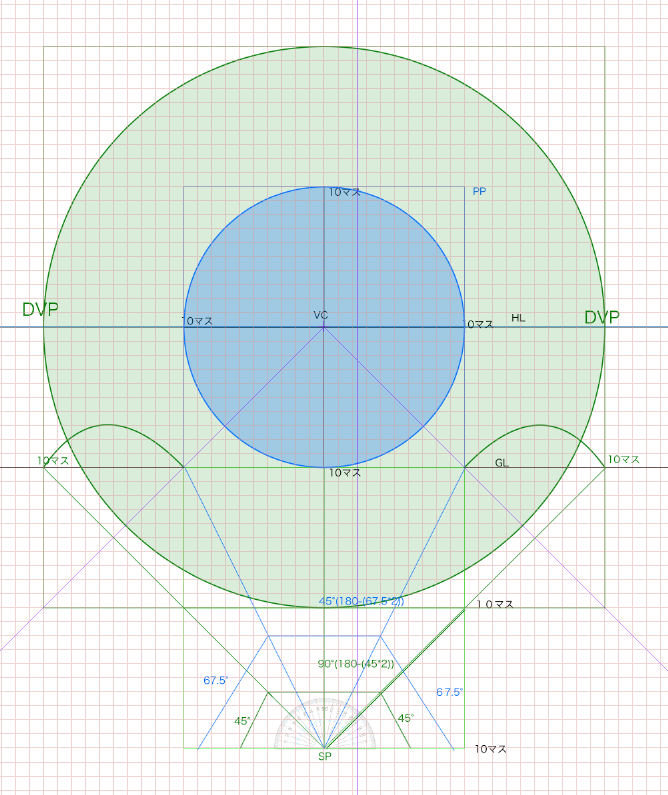
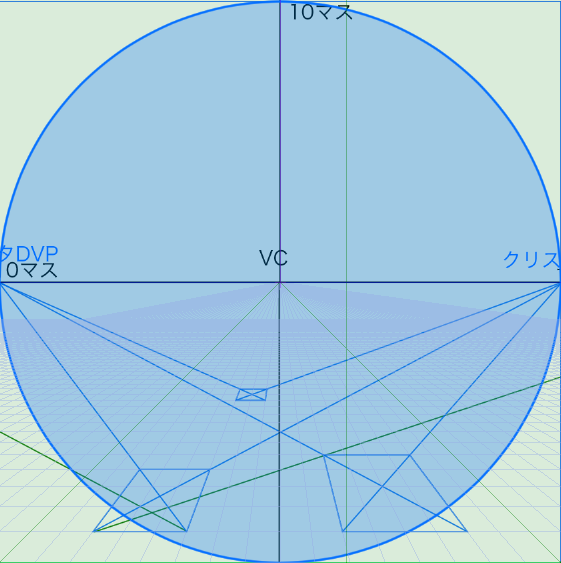
そしてクリップスタジオの対角線の消失点がどこへ向かっているのか再度見てみます。
対角線の消失点は視円錐45度の位置にあることがわかります。

つまり画面の両端にあるわけです。
今までは画面外にDVPをつくったほうが自然に見えると並んできました。どうしましょうか。
そこで二点透視図法をレイヤーにさらに加え、90°視円錐内のDVPへと線を伸ばしてみます。二点透視図法の消失点はクリックすれば簡単に移動でききます。初期位置はやはりキャンパスサイズの両端でした。なので90°視円錐内に移動します。
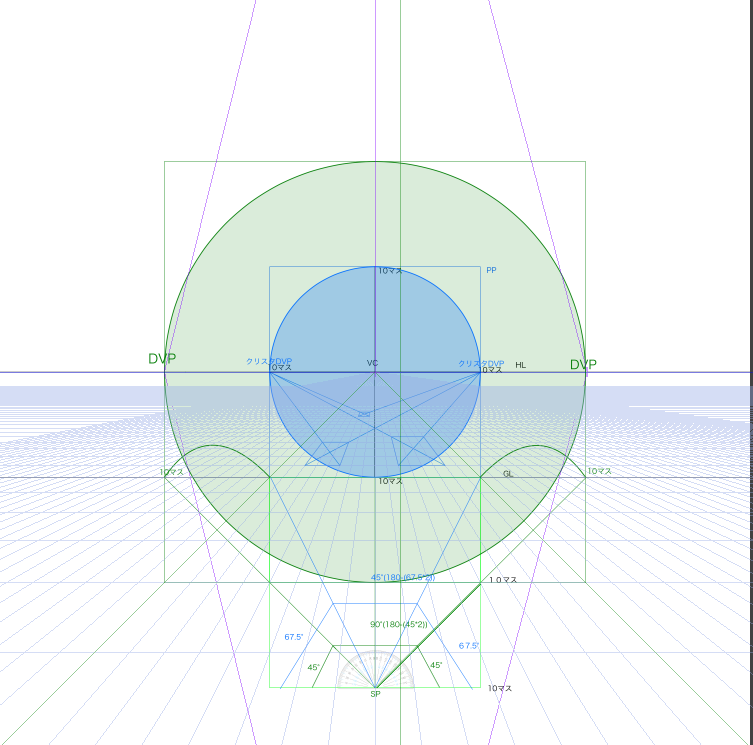
この線に従って立方体を画面内に作成してみます。
DVPが画面外にあるのでこうなります。
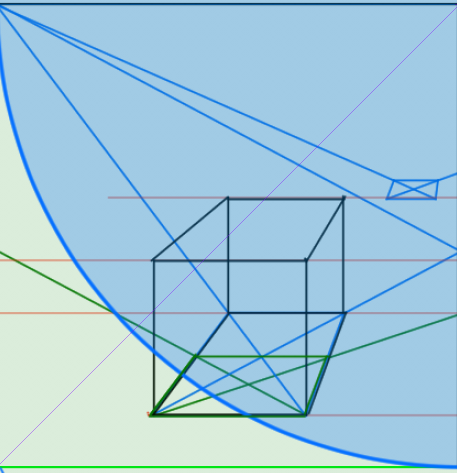
奥行きの見え方がかなり違うことがわかります。

これが対角線の消失点45°の立方体です。
これが対角線の消失点(視円錐90°)の位置の立方体です。
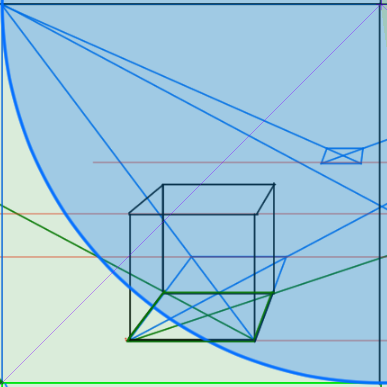
どちらが自然に見えるかという問題になってきます。参考書いわく、対角線の消失点は画面外にあったほうがいいくらいですね。なんとなくDVPが画面内にあると歪んで見える気がしなくもないです。
クリップスタジオペイントの一点透視図法の使い方:対角線の消失点45°(画面外視円錐90°)の設定方法
とりあえず一点透視図法の場合はデフォルトで対角線の消失点が90°の位置にあるみたいなので、二点透視図法のレイヤーを加えれば解決です。
A4の場合を想定してみます。例に従って適当に画面の半分くらいの位置に対角線の消失点を設置します。二点透視図法の消失点はデフォルトでキャンパスサイズの両端なので、画面外視円錐90°の位置にくるように設定します。
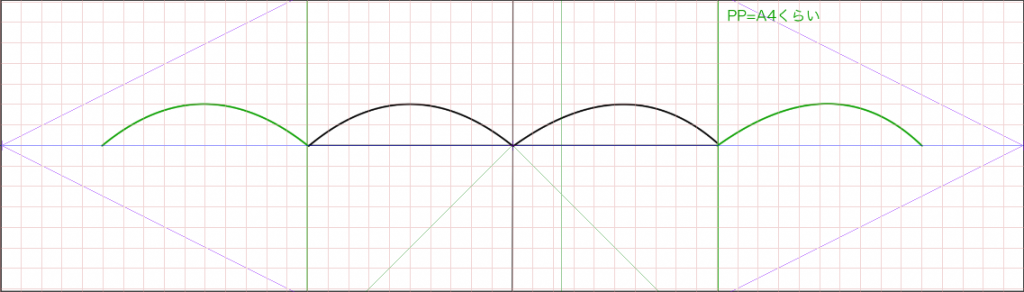
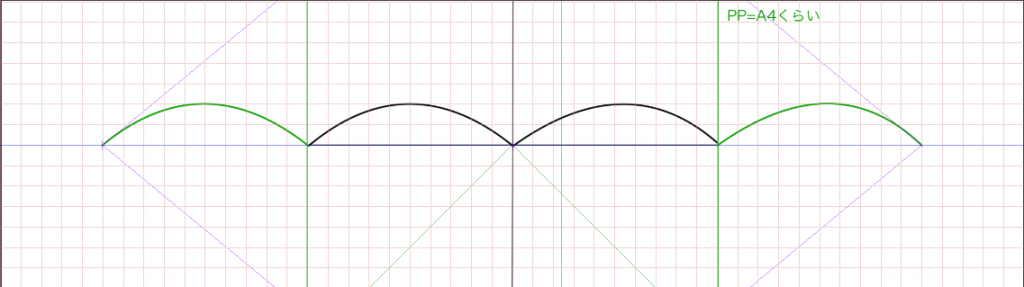
あとはもうキャンパスサイズを元のA4に戻して大丈夫です。
あとは勝手に二点透視図法のパース定規が対角線の消失点へ向かっていってくれます。
これを先程のキャンパスサイズに戻すとこうなります。
追記です。キャンパスサイズでもっと簡単な方法も載せておきます。
幅が842ピクセルです。対角線の消失点を中央から数えて842ピクセルが好ましいです。つまり、842/2で421ピクセル先に対角線の消失点があればいいのです。
ということは最初から横幅を842の2倍、つまり1684ピクセルで設定したらいいのではと思います。

これで設定すると以下のようになります。

そしてキャンパスサイズの幅を842に戻せばいいのです。そうすると画面外に消失点を設定できます。

グリッドが一致して便利ですね。

参考・引用文献
・『パース教室』ロビー・リー(ボーンインクデジタルインク)(p,rと文中では略します)
・『how to draw』スコット・ロバートソン(ボーンデジタルインク)(h,sと文中では略します)
・『パース!』デヴィッド・チェルシー(マール社)(p,dと文中では略します)
・『パースの技法: マンガでわかる遠近法・構図』染森健一(p,sと文中では略します)
・『現代パースの基本と実際』,山城,グラフィック社(g,yと文中では略します)
コメント
この記事へのトラックバックはありません。




 (wiki-正六面体)-立方体
(wiki-正六面体)-立方体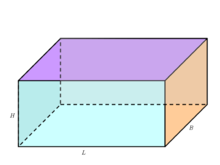 (wiki-直方体)
(wiki-直方体)







この記事へのコメントはありません。