目次
パースにおける立方体の球体は正面以外、すべて歪んで見える
まずパースの基本として中央から外れるほど物体は歪んで見えます。こうした基礎は立方体を描けば理解できます。ここでは一点透視図法を用いて考えてみます。
パースの基本的な作り方とクリスタのパースの使い方はここでは省略します。重要なのは中央から外れるほど物体は歪むということです。パースなんて作れなくてもこういったことを理解していれば絵の上達に役立てるはずです。
精密なパースよりも、自然に見える歪み方をうまく自分で編み出せるほうが絵のすごさは出ると思います。絵の正確さと絵の凄さは別物です。正確に描けるからすごいというわけではありません。
一点透視図法における立方体の歪み
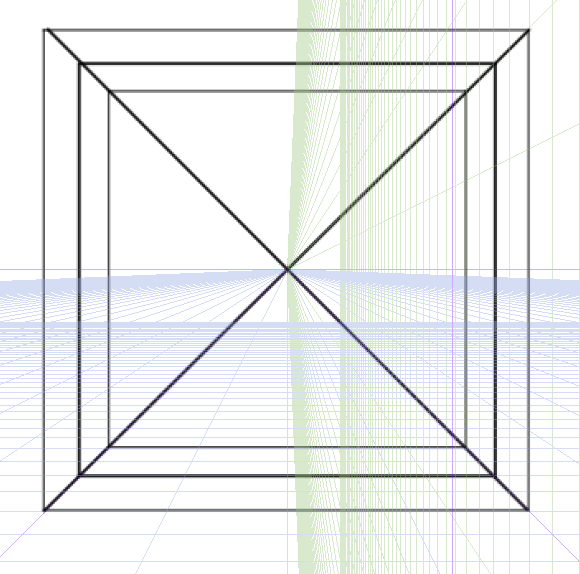
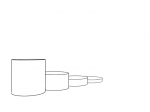
中央近くに立方体をつくってみました。一点透視図法ではこのような立方体になります。この立方体は真正面にあります。
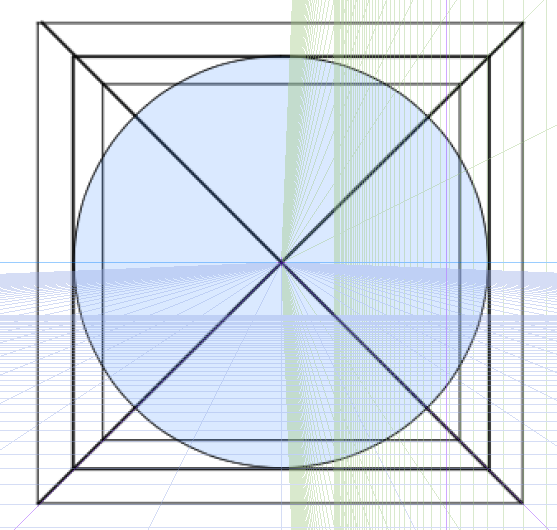
この立方体の中に球体を入れるとこうなります。
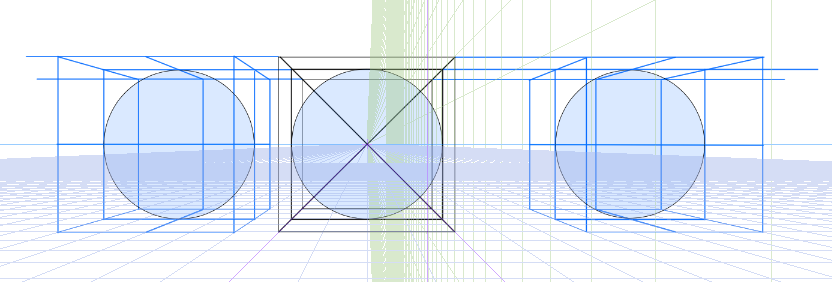
次に中央から外れた位置に立方体を作ってみます。これではい完成とはなりません。中央からズレた場合、このようにきれいな球体とはなりません。
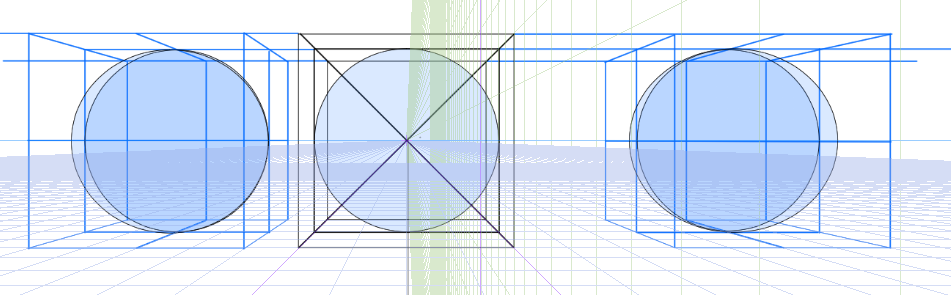
このように楕円の横幅が伸びて見えます。
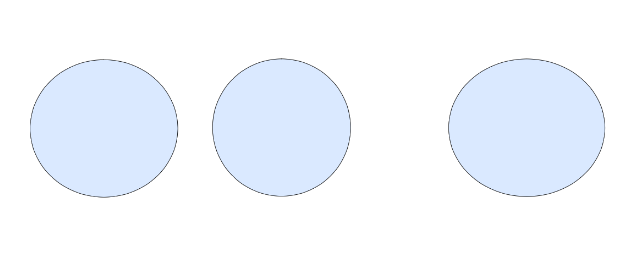
正面よりも歪んで見えることがわかります。球体だけ取り出してみるとはっきりします。
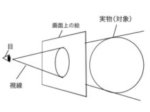
対象物を目の前に持ってきて定規で測ってみれば同じ長さですが、遠近法においては違う長さに見えるというところがポイントです。極端に中央から外れた球体をつくってしまうと歪みが出てしまうことが分かります。
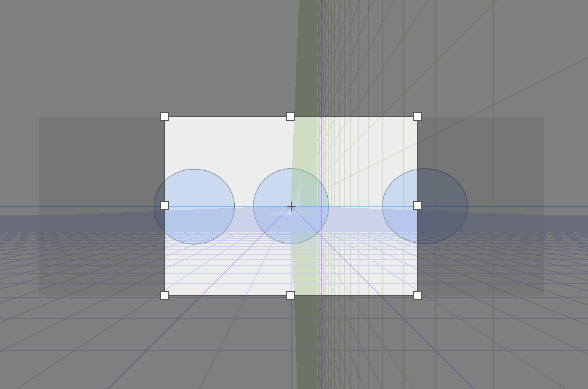
なるべくちょうどいい視円錐内に物体を置いたほうがいいですね。視円錐の説明はここでは省略します。[su_button url=”https://souzoulog.com/2017/05/20/%e3%83%91%e3%83%bc%e3%82%b9%e3%81%ab%e3%81%8a%e3%81%91%e3%82%8b%e8%a6%96%e5%86%86%e9%8c%90%e3%81%a8%e3%81%af%e4%bd%95%e3%81%8b%ef%bc%9f%e5%af%be%e8%a7%92%e7%b7%9a%e3%81%ae%e6%b6%88%e5%a4%b1%e7%82%b9/” style=”flat” background=”#0077B3″ color=”#ffffff” size=”1″ radius=”round” icon_color=”#000000″]別記事[/su_button]で視円錐について説明しています。
パースにおけ球体をできるだけ正確に描く方法
球体が中央から外れた位置にあればあるほど歪むということはわかりました。
それではどうやって歪んだ球体を描けばいいのかという問題になります。
足線法による球の作図
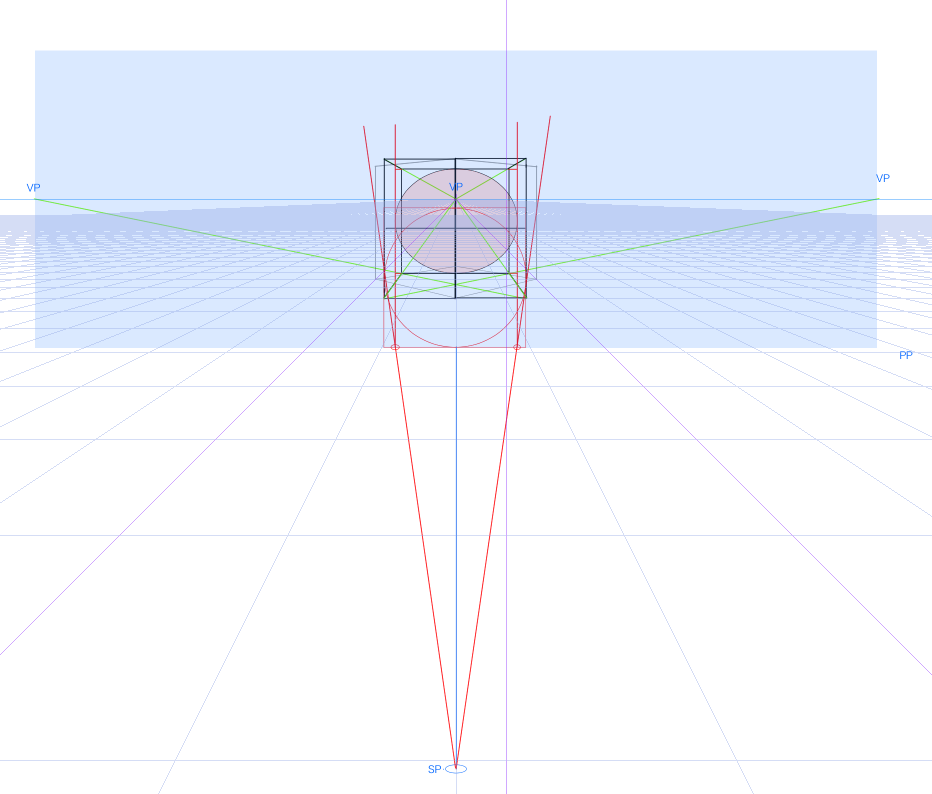
歪んだ球を描くためには足線法を使えばいいそうです。視心からPP(画面)の端までの横の長さと同じ長さを、PPの下端から伸ばせばSP(立点)がわかります。
ここでいうPPの端は、一点透視図法における対角線の消失点を意味します。二点透視図法の消失点と重なる点です。

ここで重要なことは、PPからSP(立点)までの長さと、VP(視心)から対角線の消失点までの長さが等しいということです。
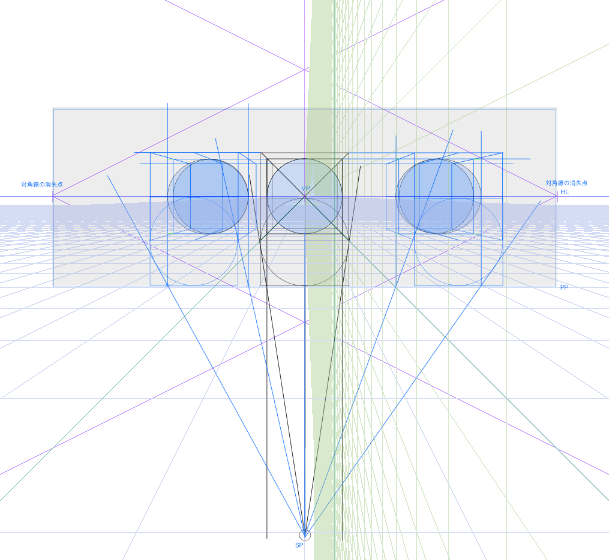

SPからの線がPPの線と重なる点にを付けて、縦に線を伸ばすと球体の横幅(長軸)がわかります。
今回参考にしているサイトは[su_button url=”https://www.persfreaks.jp/main/circle/sphere/” style=”flat” background=”#0077B3″ color=”#ffffff” size=”1″ radius=”round” icon_color=”#000000″]こちら[/su_button]です。パースについての詳しい説明がのっています。
二点透視図法における球体の扱い
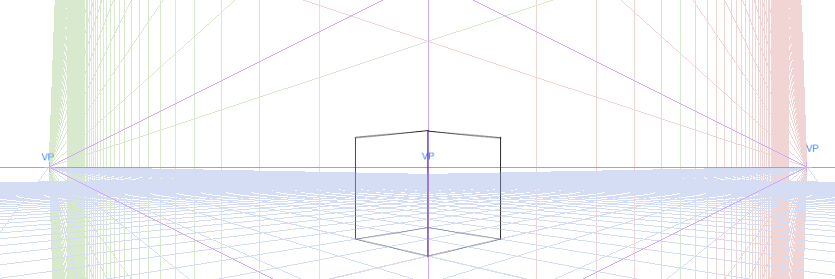
一点透視図法より複雑になります。さてどうやってつくればいいのでしょうか
立方体を回転させる
二点透視図法でつくった立方体を一点透視図法になる向きまで回転させて考えればいいそうです。
どうやって回転させればいいのでしょうか・・。
とりあえず手前の線を基準に一点透視図法に置き換えてみます。
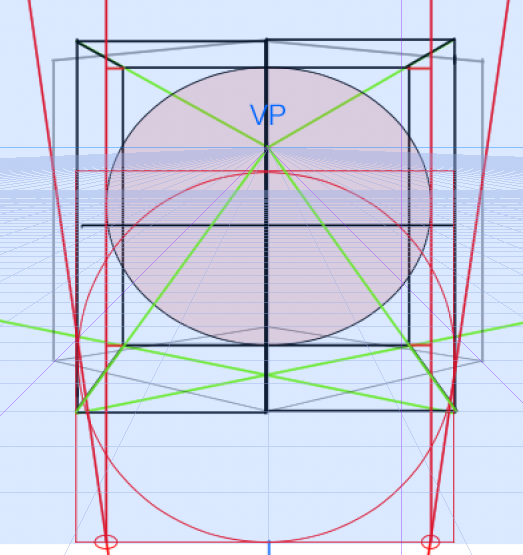
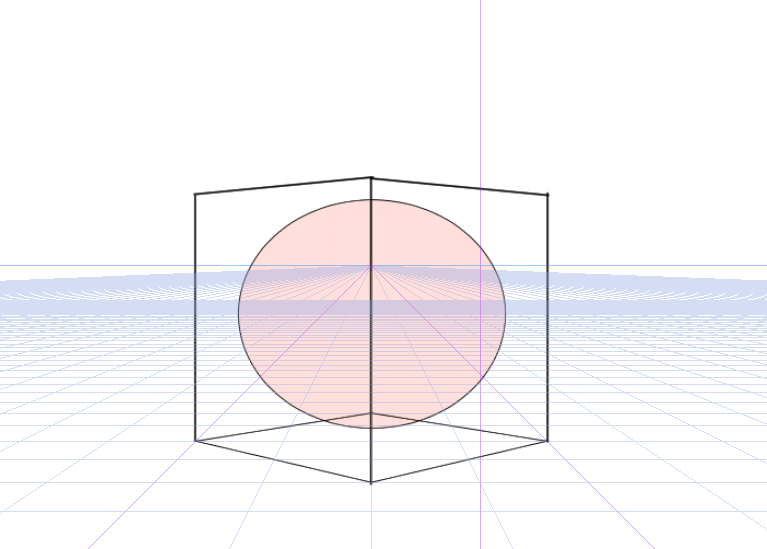
これで完成なんですかね。要研究です。
コメント
この記事へのトラックバックはありません。








この記事へのコメントはありません。