はじめに
動画での説明
・この記事の「概要・要約」はyoutubeの動画の冒頭にありますのでぜひ参照してください。
よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m
円とはなにか
円とはなにか、意味、定義、わかりやすく解説
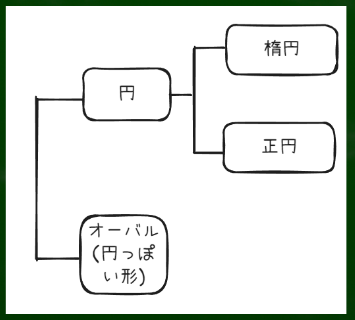
円(英:circle):日常的にいえば「まるい形」であり、幾何学的にいえば「平面上の1点から一定の距離にある点の集合」を意味する。
次の項目で扱うが、主に正円(せいえん)と楕円の二種類に区別することができる。
円の形をしている物はなにがあるか
サッカーボール、コイン、皿、ボタン、観覧車、水面の波紋、満月、水滴、年輪、車のタイヤ、ピザ、ホットケーキ・・・などたくさんある。
今までの動画ではビルやサイコロ、立方体などの「直線的」な物を扱ってきたが、自然のものは「曲線的」な丸みを帯びたものが多い。パースでは直線と曲線の2つをマスターすると、描くことのできる物が多くなるといえる。そして円は曲線の一つであると言える。
円の描き方を覚えて画力を上げる
もちろん円をマスターしただけで球体そのものが描ける訳ではないが、一歩近づいたと言える。今までの動画では直線や立方体をマスターしたが、その応用として円や球体を描くことを目指すこともひとつの選択肢となる。
もちろん、直線や立方体で妥協し、あくまでもパースでは「あたり(デッサン、下書き)」までとして、あとはデッサン力やリファレンス力(参照する力)で円を構成するという手もある(このほうが合理的だと私は考えている)。リファレンスの中にはネット、参考書籍、カメラ、実物、さらには3Dツールによる作成が含まれている。
正円と楕円の違いとはなにか
正円(真円)とはなにか、意味、定義、わかりやすく解説
正円(真円):中心からの距離が完全に一定の図形。どの方向にも同じ長さの半径を持つ円のこと。軸を2つにわけても、同じ長さの軸ができる円のこと。正方形にぴったり収まるイメージ。例:コイン
楕円とはなにか、意味、定義、わかりやすく解説
楕円(英:ellipse):2つの焦点からの距離の和が一定の図形。正円をある方向に引き伸ばしたり圧縮したりすることでできる円のこと。軸を2つにわけるとすれば、長軸と短軸がある円のこと。例:ラグビーボール
もちろん、完全な正円などないように、完全な楕円というものも現実にはほとんど存在しない。世の中のほとんどのものは厳密には綺麗な円っぽい形、楕円っぽい形というものがあるだけである。
もちろんこれは極論であり、百円玉もよくみればギザギザしていたり欠けていたりする、画像は拡大すればドット単位でずれがあるといった人間にはほとんど日常生活においては視認できない、あるいはしないほどの近似のものがある。
そこまで気にする問題ではない。逆に言えば、そこまで神経質に完璧に線を構成する必要がないということでもある。神経質になるあまりに絵を描くのが嫌いになったり、遅くなったりすることのデメリットは大きい。常に完璧なほど美しいというわけでもない。
オーバルとはなにか、オーバルと楕円の違い、円との違いとは
オーバル(oval):楕円や円に近い形のこと。ラテン語で卵を意味している。我々が見えている殆どの形は厳密にはオーバルである(正円に見えるものも、ほとんど左右対称に近いオーバルにすぎない)。
ここでは「楕円や円に近い形」の総称として扱う。
たとえば卵は楕円っぽい形ではあるが、楕円のように綺麗な左右対称ではない(対称軸を一つしかもたないなど)。
長軸線と短軸線
長軸線と短軸線の違いとはなにか、意味、定義、わかりやすく解説
軸線:楕円を分割する線であり、つねにもう一本の線に対して直角の線。長軸線と短軸線の2種類がある。
長軸線:楕円の最も長い部分を通る線分のこと。
短軸線:楕円の最も短い部分を通る線分のこと。
軸線と正円の関係
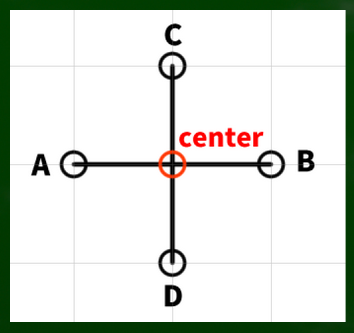
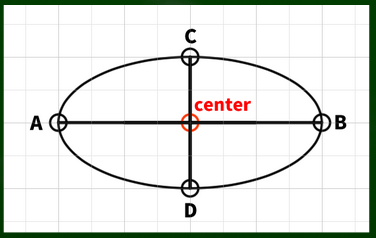
たとえばこのような十字があるとする。それぞれ90度の線、つまり直角の線である。もちろん十字自体が斜めになったりしても同じである。お互いの線にとって相対的に90度であればいい。
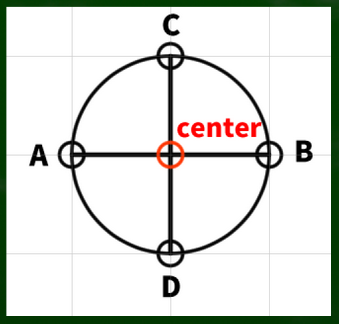
ポイントは中心(center)から同じ距離にそれぞれの点があるということである(中心からの距離が同じ)。
AB線も、CD線も中心から同じ長さのため、長軸と短軸という区別がない。
したがって、この軸線から構成される円は基本的に正円となる。
軸線と楕円の関係
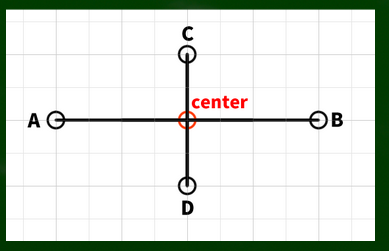
AB線をCD線よりも長くすると、AB線が長軸線となり、CD線が短軸線となる。
このケースであっても、それぞれの軸線は左右対称であるという点がポイントである(中心からそれぞれ同じ長さで構成される)。
長軸線と短軸線という区別が可能であり、さらにそれらの軸線が中心から同じ長さだけ伸びた線である場合、楕円を構成することができる。
要するに、短軸線と長軸線の長さの比によって、楕円の形状が決まるというわけである。
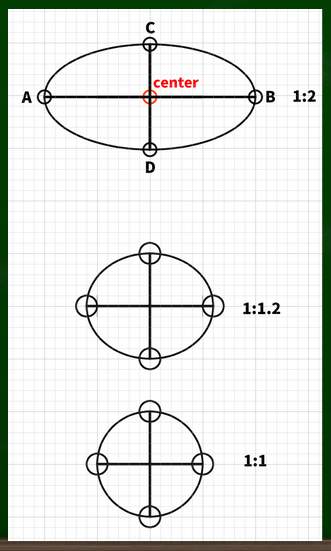
それぞれの軸線の比率が1:1(1/1)の場合、つまり1に近づくほど、正円に近い円だといえる。
正円と楕円とオーバルの違い、境界について
先程の楕円の場合は1:2なので、½=0.5となり、1とは離れてしまっていることが分かる。
仮に1:1.2にすると、すこし正円に近づく。
もし左右対称ではない線の場合、それを楕円の軸線とは表現しない。
ただし、自然には完全に比率が1の円は存在せず、0.09や0.94など、不完全な円としてしか存在しない。
楕円も同じであり、完全に左右対称の二軸ではなく、中心から左に1、右に0.9といったものも我々はきれいな楕円とみなしてしまうかもしれない。
ここが大事なのだが、我々は完全な円や楕円よりも、すこし不完全な円や楕円を美しいと感じる場合もある。デジタルの綺麗で無機質な線よりもフリーハンドで描いた線を美しいと感じた経験があるはずである。
絵は1に近づけば近づくほどいいというわけではなく、必ずしもパースに正確であればあるほどいいというわけではないことを抑えておこう。ただし、建築や製品開発では正確さが重要になることがあるので注意しておく必要がある(美しさよりも製品が機能するかどうかのほうが重要になりがちだから)。
たとえば左に3で右に1のような軸線から構成される円は楕円ではない。楕円っぽい円であり、オーバルだといえる。※もっとも、このようなかたちになるかどうかも正直よくわからない(ここでは重要ではない)。
正円は透視図法でほとんど楕円に見える
平面図で正円を見たケース
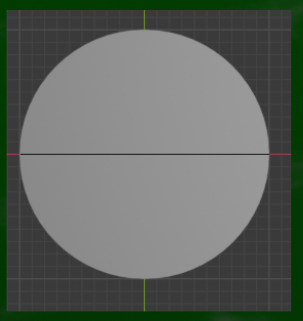
たとえば平面図で正円を見ると、このようにきれいな円に見える。楕円には見えない。
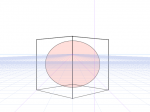
一点透視図法で正円を見たケース
一点透視図法の画面で見てみよう。たとえばこのような角度で正円を見ると、楕円にしか見えない。
正円をいくら増やしても、楕円にしか見えない。
床にある正円を人間が通常の角度で見る場合は、正円に見えないことが多い(真下の床を見るケースなどは除く)。しかし正確に言えば楕円にも見えないのではないだろうか。なぜなら左右対称に、同じ幅に中心から線が伸びてない(ように見える)からである。
もちろん自然な感覚として楕円には見えるのだが、楕円の定義としては誤りであるということになる。なぜならこの一点透視図法の画面においては、奥へ行けば行くほど線が短くなって見えるからである。そのため、軸線が中心から同じ長さで伸びているとはもはやいえなくなる。
たとえば簡単な立方体を一点透視図法で描くだけでもそのことがわかる。奥へ行けば行くほど、実寸では(平面図では)同じ長さの面が短くなっていくように見える。
これは立方体における面でも当然生じていることであり、そのために左右対称の軸線ではなくなってしまう。
ようするに、実寸では正円や楕円であっても、われわれがそれを我々の視点で自然に見るときには正円や楕円には見えなくなっているということである。
我々が見ている丸っぽい形、円っぽい形はすべてオーバルであることがわかる。実寸では左右均等だからといって、画面に左右均等に描いてはいけないのである(例外はたくさんあるが)。この感覚をもっていることは重要である。
左右均等に見える透視図のケース
もちろん左右均等に限りなく近く見える視点もある。たとえば一点透視図法の場合は正面は収束しないため、平面図、実寸通りの比率に見える。
ただし、正面以外の面は収束するので、すべてオーバル(楕円っぽい形)に見えてしまう。
もちろんパースによってはほとんど左右対称にみえる場合もあるが、そうした立体感覚の機微を自然に身につけるためにもパースを学ぶ必要がある。
パースを使わなくてもパースを意識して自由に紙に絵を描くことができるようになることが理想だと言える。自然な形を脳内に埋め込むのである。その意味で、パースを学ぶ作業はデッサンと同じだといえる(勉強の知識ではなく、体験による知識であると言える)。
先程の画面でも、正面の場合は一点透視図法ではきれいな円が見えることが分かる。ただし側面では実寸では正円であっても、オーバルに見える。
二点透視図法で正円を見たケース
もちろん二点透視図法に切り替えた場合、さきほどの正面の円も、オーバルに見える。
三点透視図法で正円を見たケース
三点透視図法も同様である。
とはいえ、オーバルなのか正円なのか、微妙に判定しづらい場合がある。この微妙な違いに対するセンスを身につけるためにも、パースを(アナログでも)勉強する必要があるといえる。
パースの感覚を言語化するとは
パースの感覚を言語化すると有用かもしれない。たとえば一点透視図法の場合、正面以外の面の円は遠くに行けば行くほど細く見える。言い換えれば、正円はより楕円に近づくと言える。
この法則を覚えておくと、アナログで自由に用紙に絵を描く場合に役立つかもしれない。
この法則は二点透視図法でもあてはまる。奥へ行けば行くほど、細く見えていく。
こちらは三点透視図法のケースである。一点透視図法よりは細長く見えない理由は、一度に見えるオブジェクト(対象、物)の数が少ないからだろう。一点透視図法でいうところの、手前側のオブジェクトしか見えていない。
画面外のオブジェクトも表示するとすこしわかりやすくなる。
一点、二点、三点のそれぞれの変化の違いは微妙に違う。それらを抑える感覚、言語化できる能力も必要になるだろう。
そもそも画面の構成に対しての理解が前提として重要になってくるのかもしれない。
たとえば見えている風景をどの範囲まで切り取るのか、どういう角度で切り取るのかといった理解がないと、どれくらい細くなるのか、どう形状が変化するのかを理解することは難しい。
まずは立方体でその変化の感覚を複数の基本パターンで試して、身体感覚として身につけることが必要になる。たとえば一点透視図法で上から見た場合はこれくらい変化する、二点透視図法でこのくらいの角度で見た場合はこれくらい変化する、という感覚を体に覚えさせるイメージとなる(この意味で、デッサンと近い)。
レントゲン技師は鍛錬によってたんなる染みを病原と即座に見なせるようになるというが、絵師も同様ではないだろうか。
楕円の中心はどこにあるのか
平面図における正円や楕円の中心
これ濃厚目は意外と難問である。なかなか理解しにくい。人によっては何を言っているかわからない人もでてくるかもしれない。
しかし画像で見ていくと理解はよりしやすくなる。
まず、平面図における正円の中心は当然、ここにある。つまり、正方形の中心と同じ位置であり、対角線が交わる位置にある。
違う言い方をすれば、実物としてはこの位置に中心があるということになる。また、正方形の中心とも位置が重なる。
透視図において楕円の中心は、収まる正方形の中心にあるように見えない
しかし透視図においては違って見えてくる。
- 透視図においては奥へ行けば行くほど幅が短く見える。
- 透視図においては対角線の交わる位置は平面図と同じように(実寸において)均等ではない。
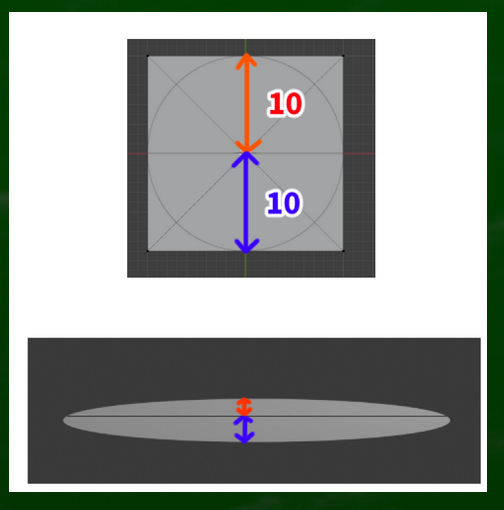
たとえば平面図において中心から奥への線が10センチだとすれば、中心から手前への線も10センチとなる。
つまり割合は(実寸において)1:1である。定規で測っても同じ比率ということになる。
たとえば透視図においては、(平面図において10センチ:10センチであるにもにかかわらず)中心から奥への線が8センチ、中心から手前への線が9センチに見えるとする。この場合に割合は8:9に見える(比率の数字は適当)。
実寸大にも見えず、実際の比率と同じようにも見えないというわけである。
楕円における2重の錯覚
さてここからが重要である。
- 透視図における正方形の中心に見える点は、正円の中心である。正方形が奥へ行くほど短く見えるように、円も奥へ行くほど短く見える。したがって、円の中心はやや奥側になる(手前が長く、奥が短く見えるため)。
- 透視図法の原理にもかかわらず、実際の楕円の中心は正方形の中心と同じ位置にあるようには見えない。実際の中心は正方形の中心よりもすこし手前にあるように見える。
正直、混乱する。「実物より違って見えるもの」からさらに違って見えるというように、二重に違っているというややこしい構造になっているからだ。また、言い方もややこしい。平面図では正円に見えるが、透視図では楕円に見えるからである。したがって、円の中心と楕円の中心が違うという言い方をすることもできる。言い換えれば、実際の中心、原理の中心、見え方の中心の違いともいえる。
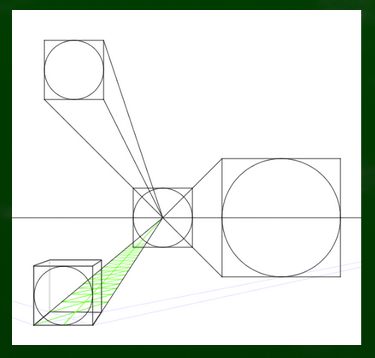
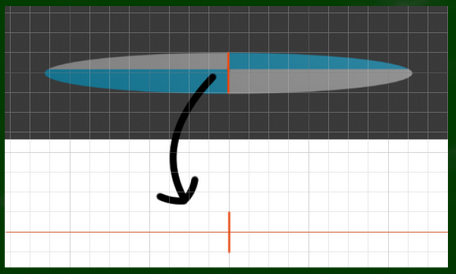
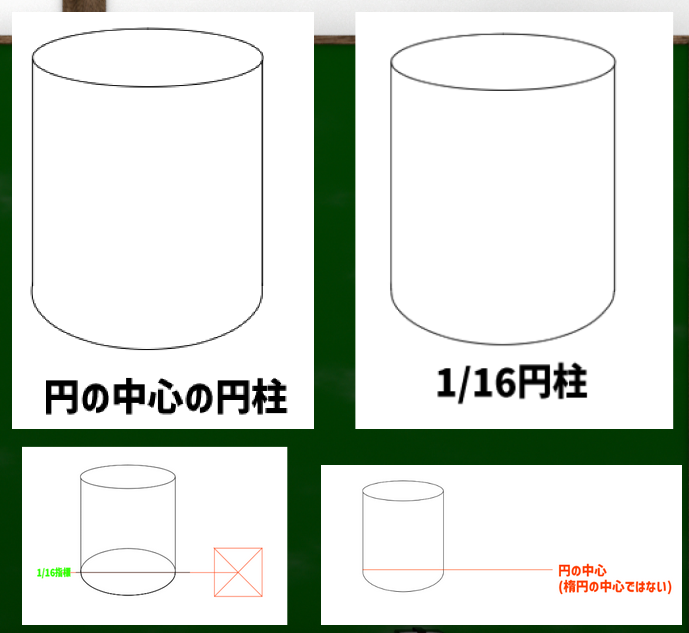
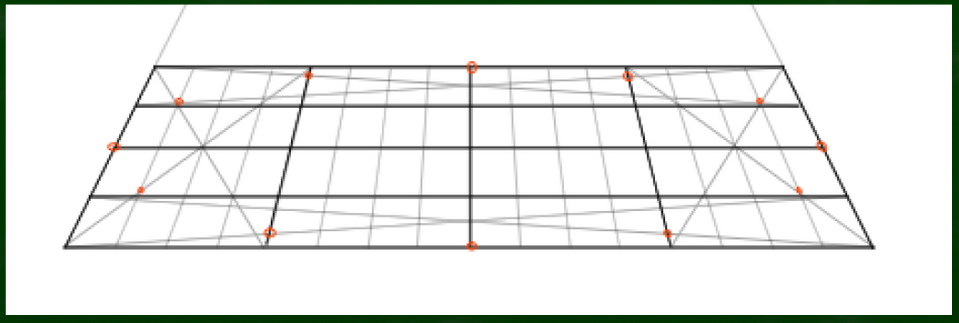
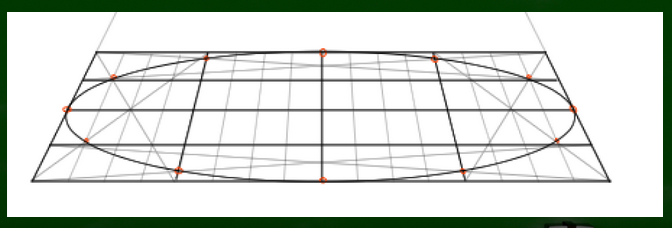
この画像を見てもらえればすぐわかるのではないだろうか。左の画像は平面図における実寸の分割線である(正円の中心)。右の画像の黒い線は透視図における正方形の分割線である(原理の中心、ここにあるはずの正円の中心)。緑の線は中心に見えてしまう線である(見え方の中心、楕円の中心)。黒い線の位置が円の中心であるはずなのに、円の中心には見えないというわけである。円の中心はすこし手前に見える。
すこし複雑なのでもう一度整理して言い直そう。まず、平面図における黒い線がこちらである。
平面図なので当然、1:1の位置にくる。つまり実物と同じ比率で円が構成される。
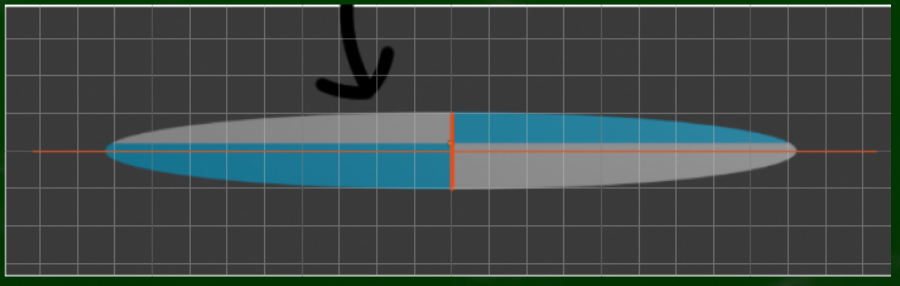
透視図法でさきほどの円を見てみると、黒い線の位置が円の中心には見えない。円の中心とは要するに一番盛り上がっている、幅が広い位置である。しかし黒い線よりもどうも幅が広い線があるように見える。
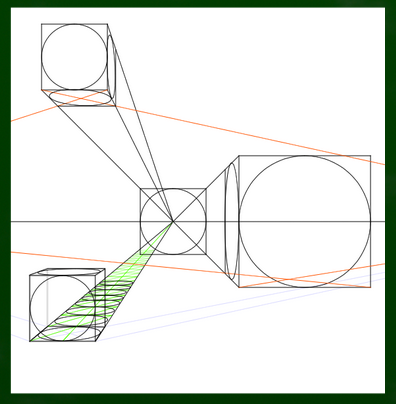
下の画像は二点透視図法だが、やはり黒い線よりも幅が広い線があるように見える。
絵を描く人が重視するのは「透視図法において中心である位置」ではなく、「我々人間の目において自然に、中心に見える位置」である。建築家の人にとってはある意味では透視図法における見え方はあまり大事ではなく、まずは平面図においてどのように構成されているかが第一だと言えるかもしれない。自然に見える建築をしても実際に歪んでいたら建物が不安定になる。
絵を描く人たちは楕円の中心がパースにおいてどの位置に、どの比率において一番自然に見えるかを学ぶ必要がある。言い方を変えれば、絵を描く人たちはマジシャン(錯覚を利用する技術者)であるともいえる。
透視図法における楕円の中心は、実寸の半分の位置にある?
- 平面図における正円は、各軸線の比率が1:1である。
- [第一の錯覚]透視図における正円は、各軸線の比率が1:1ではなく、手前が少し長く、奥が少し短く構成された位置に中心がある(すこし奥に中心がある)。
- [第二の錯覚]透視図における正円の中心は、(2の中心ではなく)透視図において見えている軸線の実測の長さのちょうど半分の位置にあるように見える(すこし手前に中心がある)。
要するに、この長さを定規で測って、半分の位置に我々が自然に見える円の中心があるということになる。
実際に合わせてみると、確かにこの位置が「われわれが自然に中心に見える」気がする(最も幅が広いように見える)。
だいたい1/16くらい透視図法における中心位置から手前にある
とはいえ毎回測るのは大変なので、だいたい1/16くらい透視図法における中心位置から手前にあると暫定的に法則化しておくことにする(正確な数値ではなく、あくまでも暫定である)。※これも正確にやると大変なので、ざっくりでもいいかもしれない。
透視図法における正円の描き方
平面図における正円の描き方
まずは平面図でそもそも円をどうやって描くのかという問題がある。デジタルなら円ツールで描けばいいし、アナログならコンパスで描くのが楽だ。
とはいえそれは平面図の話であり、透視図に応用させることが難しい(コンパスを透視図に活かす方法もあるかもしれないが、今回は触れない)。もちろんデジタルではパースツールで円を描くという方法があるが、このシリーズは基本的にアナログでもできる方法を扱っているので触れない。
今回は幾何学的な知識を用いて円を構成したいと思う。まずは正方形を作り、その正方形を分割していって円の指標を探そうという試みである。
そもそも正方形はパースにおいてどう作るのか、という点に関しては以前の動画を参照してほしい(一点、二点、三点透視図法のそれぞれで立方体を構成する方法を扱っている)。
まずは平面図から扱う。
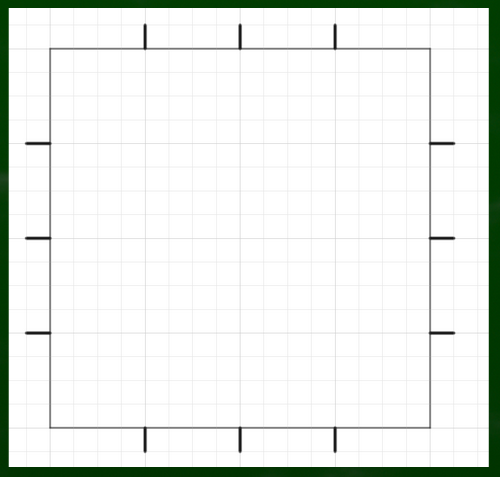
一辺が実寸通り同じ長さの正方形を用意する。
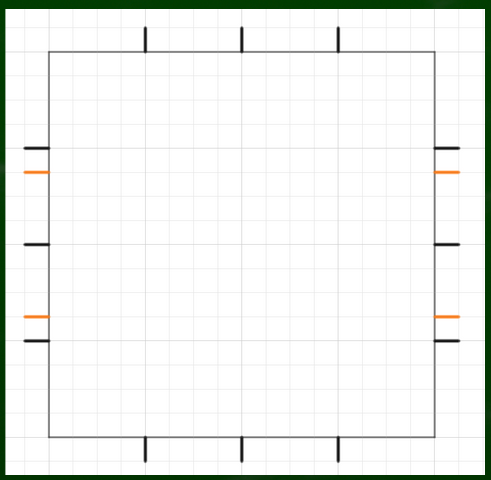
さらにここから8分割する。定規で測ってもいいし、分割線を利用してもいいだろう。
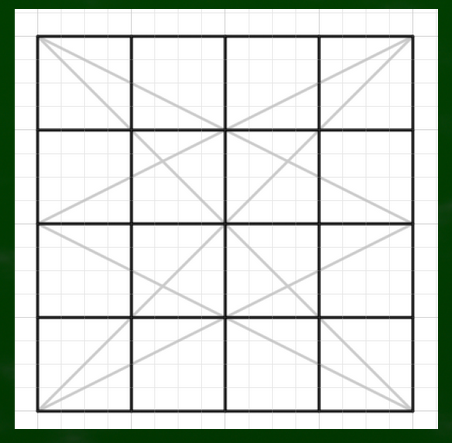
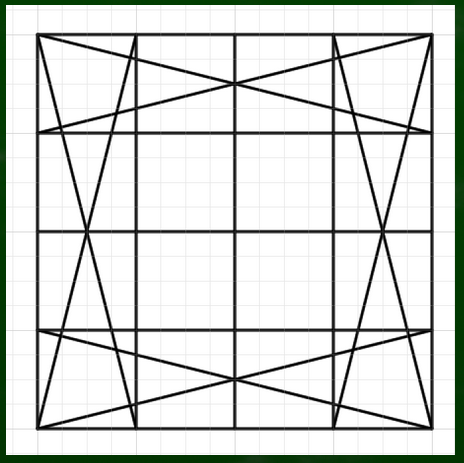
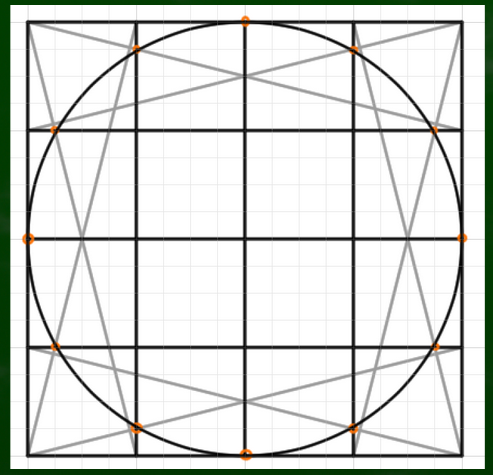
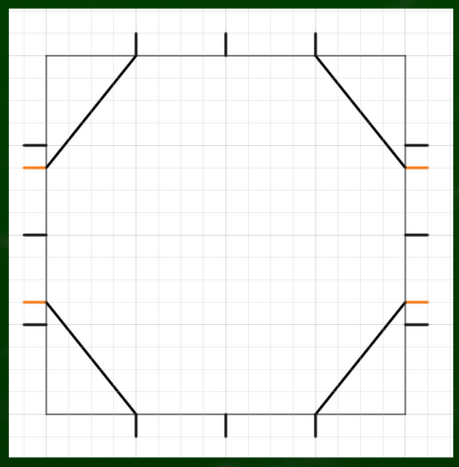
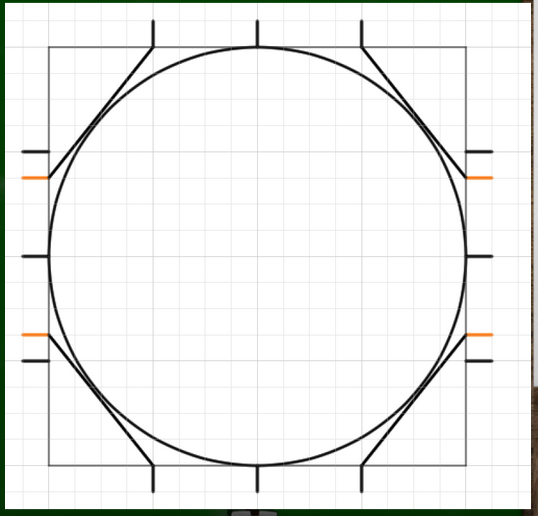
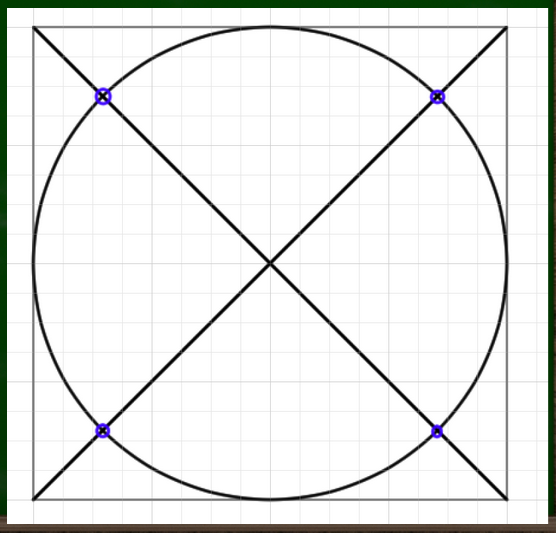
外側のマスにそれぞれ対角線を引いていく。
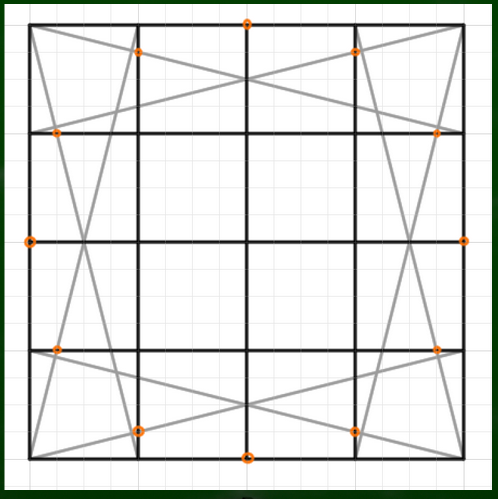
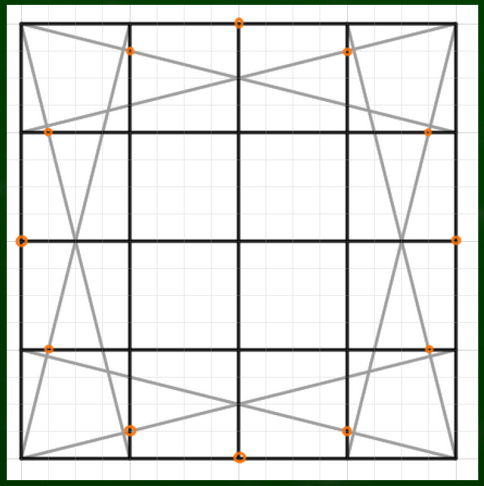
分割線といちばん近い角から伸びる斜線が交差するところに印をつけていく。
今つけた印を目安に構成していけば比較的綺麗な円が描けるというわけだ。
とはいえ、めんどうだなと感じてしまう。
そもそも直線以外を幾何学で構成するというのは複雑すぎて向いていない気がする。あくまでもこれくらいのサイズというアタリとして利用するべきだろう。
昔、5344という法則を見つけたことがある。これも正確ではなくアタリとしてしか利用できないが、なかなか便利だと思った。
まずは適当に正方形を4分割する位置を見つける。別に印をつけなくとも、頭の中でつけるだけでもいい。
さらにそこから、1/4を足して5になる位置を4つ探していく。
5の位置から4の位置に向かって線をそれぞれ角でひいていくだけで終わりである。これが円を描く際の目安になる。
円を構成するとこのようになる。これが実用的かどうかはわからない。このようにして自分なりの楽な方法を見つけてほしい。
他に有名なものとしては、中心から2/3の位置に印をつけるという方法がある。
この方法が一番やりやすいかもしれない。
しかし斜線から2/3もしくは1/3を見つけるというのは意外と感覚としては難しい。用紙を回転して直線として扱うと、もうすこし分割しやすくなるかもしれない。
ちなみに正方形の斜線(対角線)はルート2なので、一辺を1とすれば1.4くらいである。つまり、中心から2/3とは、ルート2の半分の2/3であり、およそ0.47くらいになる。仮に0.5とすればスッキリするが、誤差は大きくなる。0.5よりほんのすこし短いという感覚を残せば、誤差はより小さくなるだろう。
そもそもデッサン力をつけて正方形がなくても任意の円を描けるようにしたらいいという意見もあるかもしれない。あるいは正方形からデッサン力によって円を描く力をつけることも可能かもしれない。
いずれにせよそれは平面図のはなしであり、そもそも目的の達成だけならばコンパスや円ツールを使えばいいということになる。今回は透視図法で使うために幾何学的な手法を学んでいる。
透視図における正円の描き方
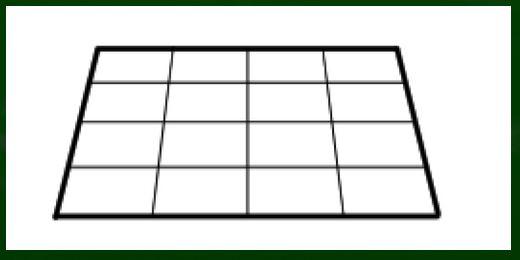
このように収束していく正方形、ようするに台形で円を描く場合は幾何学の目安が役に立つ。
もちろんこれらの形状をデッサン力で身につけることも可能かもしれないが、まずは正解の形を見て描いて覚える必要がある。
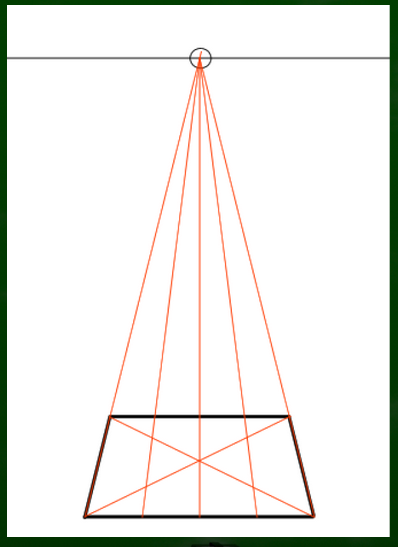
分割法を使って、8分割していく。まずは対角線で4分割する。
平面図と違い、一点透視図法の消失点に収束するように分割していくという点が重要になる。
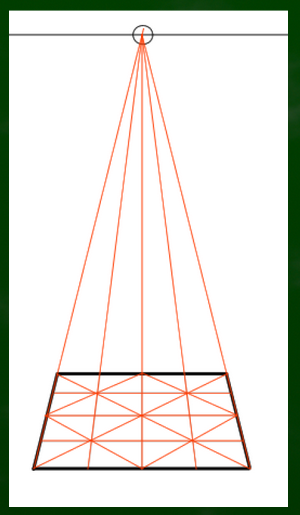
8分割するとこのようになる。
スッキリさせるとこのようになる。
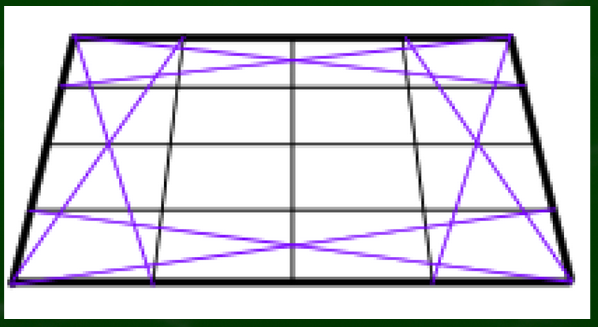
さらにここから平面図でやったように、対角線を隅に作っていく。
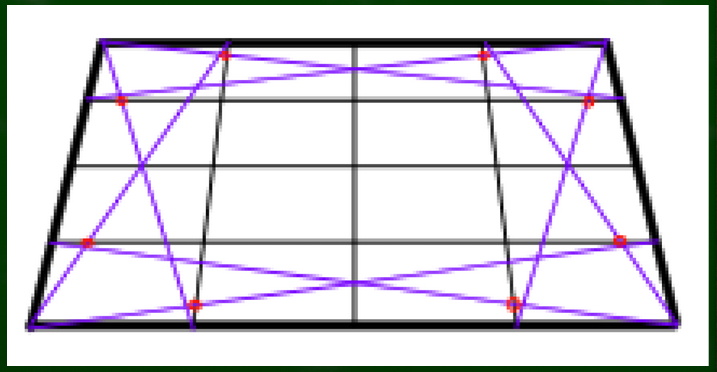
印をつけていき、それを指標にして円を構成する。
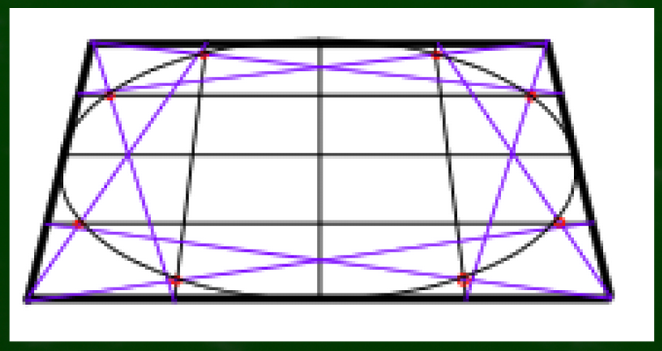
円を構成するとこのようになる。
tips、画力、立体感覚
目印があっても円を構成するのは難しい。おそらく慣れなのだろう。正確に円を描く作業はアナログでやるよりデジタルを下敷きとしてトレースするか、それを参考に描いていったほうが良いのではないかと思う。
大事なのはなんとなく正解を頭に入れて、なにもパースの設定をしていないときでも近似した円をフリーハンドで描くことのできる立体感覚だろう。そのヒント、いわゆるtips(ちょっとしたコツ)を集めていくことがアナログのパースを学ぶ理由となる。このtipsの差が画力の差となる。
ところで、あんなにややこしい話をした円の中心がズレるという話はどこにいったんだと思った人がいるかもしれない。
たしかにそうだ。いわゆる1/16指標を今回利用していない。正確に言えば、円ツールでズルをして描いてしまったので必要がなかったということになる。限られた指標の点だけを使ってきれいな円を描くことは実際難しい。もっとヒントやtipsはないのかという話になる。
円の中心がズレることと、円の描画の関係
ところで、あんなにややこしい話をした円の中心がズレるという話はどこにいったんだと思った人がいるかもしれない。
たしかにそうだ。いわゆる1/16指標を今回利用していない。正確に言えば、円ツールでズルをして描いてしまったので必要がなかったということになる。限られた指標の点だけを使ってきれいな円を描くことは実際難しい。もっとヒントやtipsはないのかという話になる。
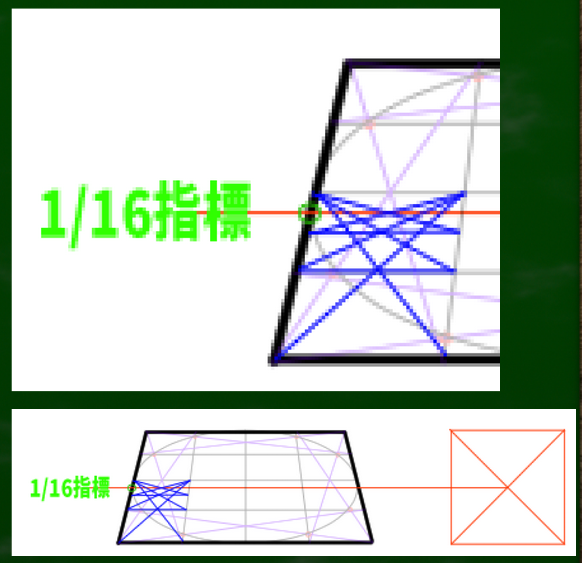
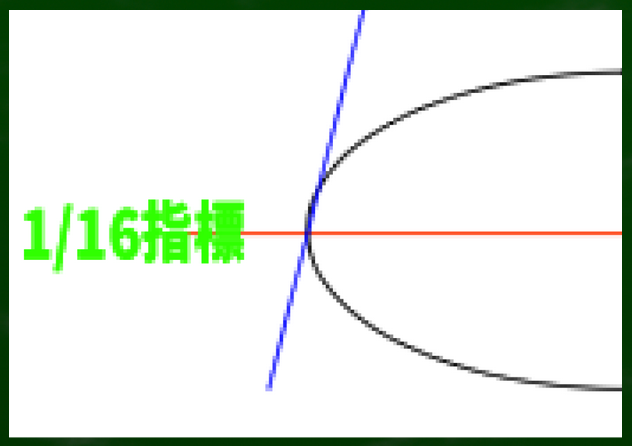
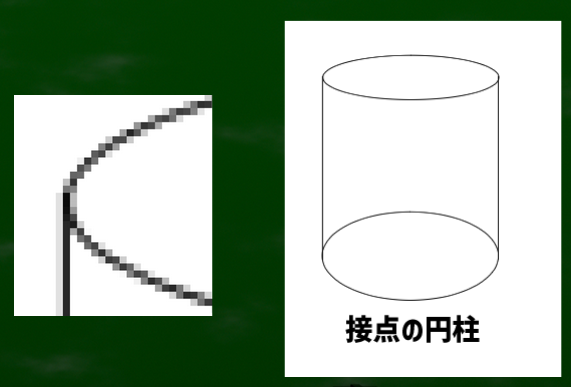
1/16指標は円を構成するときの参考のひとつになるだろう。なぜなら、その指標の位置は円の最大幅と合致するからである。すくなくとも、その点は線が急カーブしていない。
右の図は1/16の位置である。
このあたりはカーブしていないな、という指標だけでもヒントとして重要ではないだろうか。
※微分積分などの知識があると、もっと言語化することが可能になるのかもしれない
円柱における垂線はどのあたりに引けばいいのか問題(円柱の描き方)
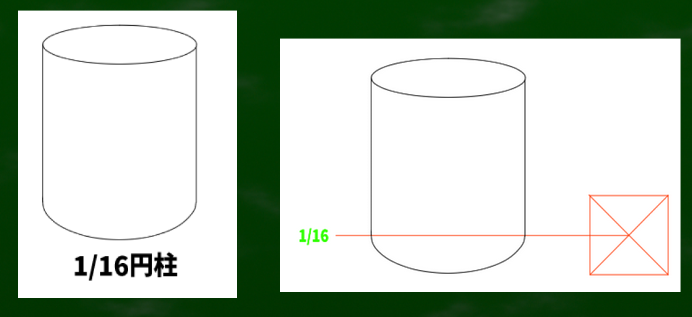
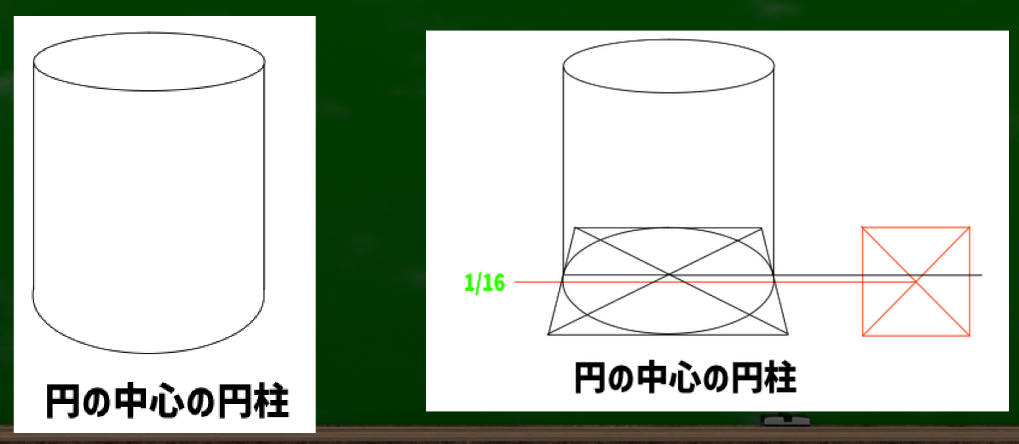
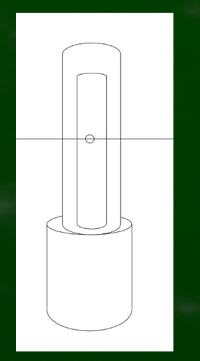
たとえば円柱を作る場合に、この指標を基準にして作ってみる(この方法が正しいかはひとまず置いておく)。
円の中心の場合はこうなる。
なんとなく1/16指標のほうが自然に見える気もする。
私の描き方や円の消し方のバランスの問題もあるので、あくまで仮説にとどめておく。
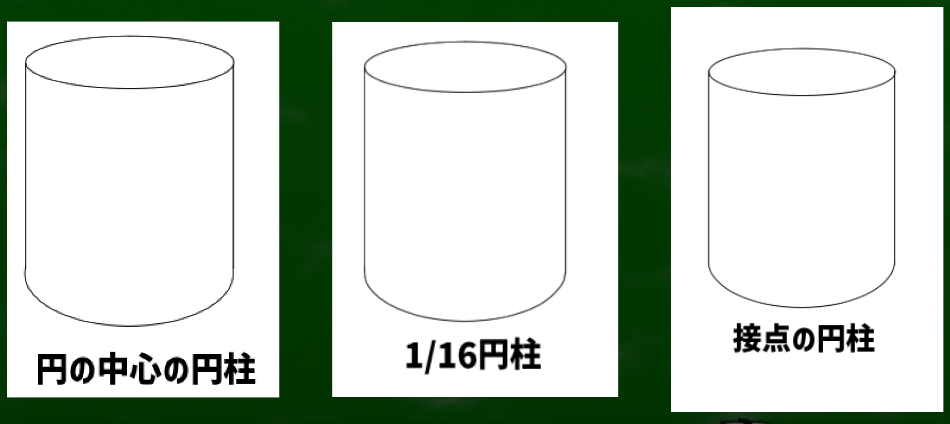
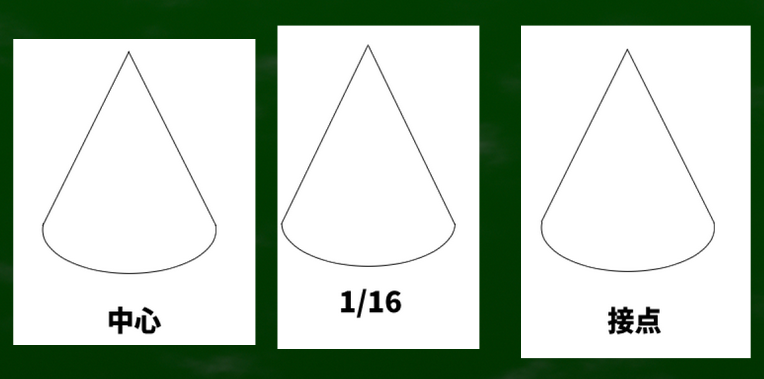
円柱を構成する際に円から円へ下ろす場合の線は3つに絞ることができる。第一に円の中心、第二に1/16の指標(楕円の中心)、第三に接点(最大幅に見える点)である。
第三の方法はようするに、柔軟に一番自然な位置にとりあえず線を引いてみるという手法である。今のところ柔軟な方法である接点のケースを最良の方法と仮定する。ただし、円柱に限っては1/16の指標も有用だと仮定できる。両者は近い点にあるといえる。
接点のケースでは、一番幅が高く見える点を選んで線を下ろしてみた。
それぞれの比較。
透視図法における楕円、三角錐の描き方
透視図法における楕円の描き方
やり方は基本的に正円と同じだと仮定していく。
たとえば長軸を2倍にすれば、楕円を構成することができる。先程の正方形を長方形にすればいい。
正円でやったように、対角線を作って指標を見つけていく。
あとは指標を目印に円を描いていくだけである(これがなかなかフリーハンドだとおそらく難しいのだが)。1/16線を今回は利用していないが、中心からすこし手前にも最大幅がくることを考慮して円を描く必要がある。
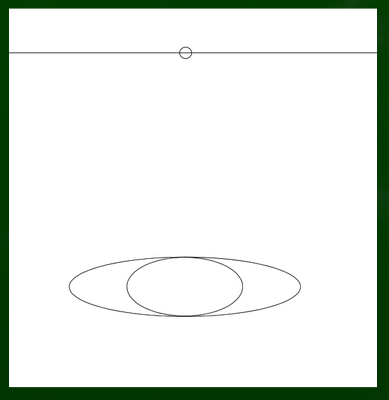
正円と楕円を並べるとこのようになる。
透視図における三角錐の描き方
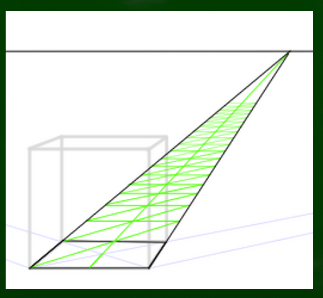
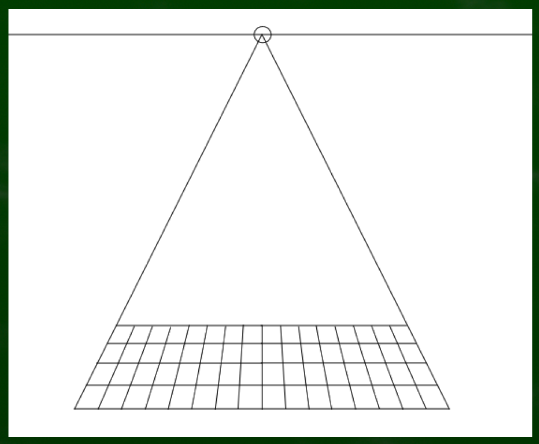
ところで、三角錐ならもっと楕円の中心が手前になるという点が理解しやすいのではないかとふと思った。
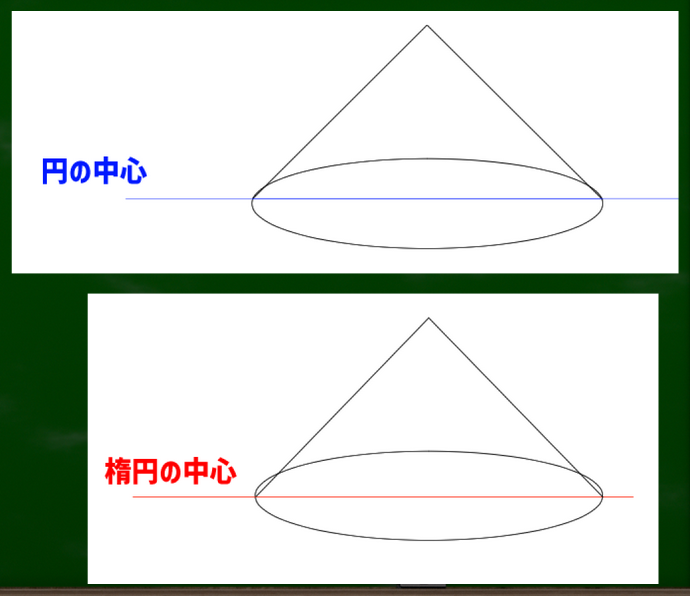
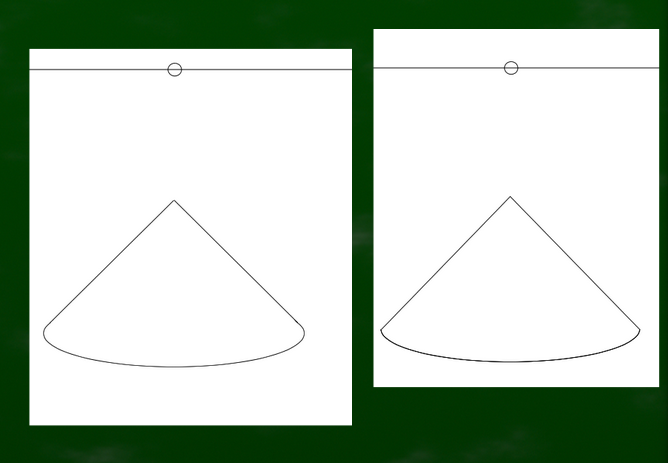
たとえば円の中心(長方形の中心)を基準に三角錐を作った場合はどうなるのか。
図にするとこのようになる。
しかしどちらのケースもどこか違う。つまり、きれいな円錐を構成できるようには見えない。
むしろ円の中心のほうが惜しい感じさえする。つまり、円錐を作る際は円の中心の手前ではなく奥を基準に構成するほうが自然に見えるのではないかという仮定が生じる。
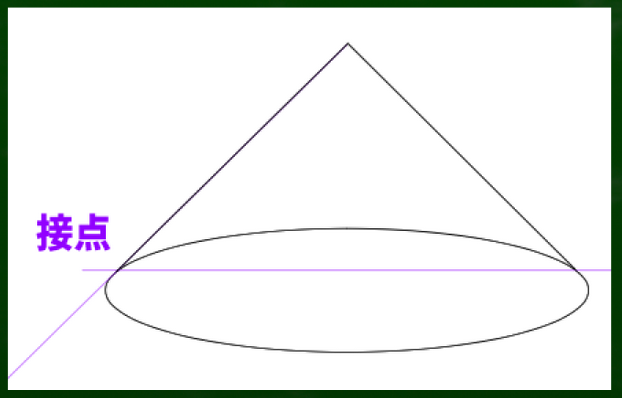
そこで、三角錐の頂点から線を伸ばしていき、最初に接する点にしてみた。
なかなか悪くない円錐ができた気もする。
この辺りは正確な理論を知るというより、どれが自分にとって一番自然に見えるのかも重要になるのかもしれない。
いずれにせよ学習のログ(履歴)を残しておくことは大事だろう。不自然なものを捨て、自然なものを選んだ先に美しいものがあるかもしれない。戻るためにもログは必要になる。
1/16ケースを用いて、はみ出た部分をすべて削除することによって対処しても、あまり自然にはみえない。
※円柱や円錐については幾何学的な理論を学んでから再度考察する必要があるかもしれない。
楕円の中心ではみ出た部分を削ったケースとの比較がこちらである。
正円で作った円柱の比較図がこちら。正直よくわからない。
自然に見える接点を自力で探すという方法をまずは最善の仮説として採用しておくことにする。
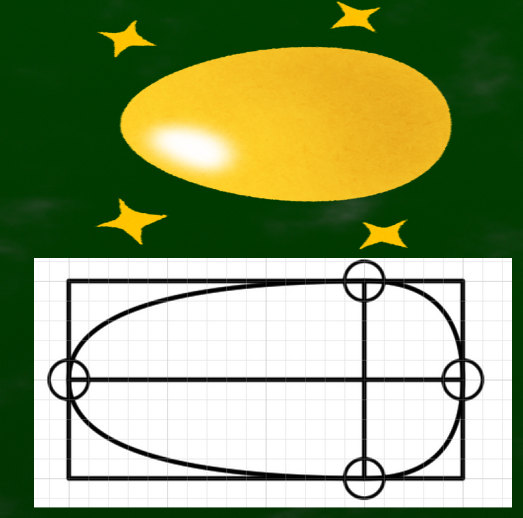
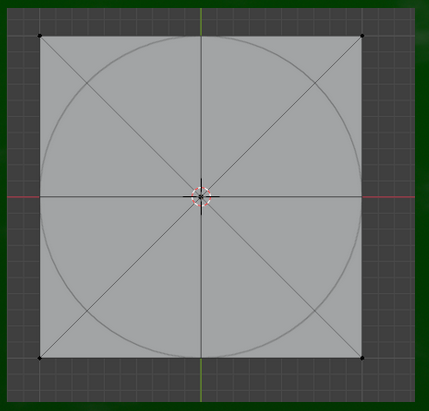
ちなみにblenderの自然な円錐はこちらである。ある意味、正解に近いものなので、こうした形を参考に自然な形を目指していけばいいのかもしれない。
※右の画像はカメラの角度や視円錐、位置などを正確に合わせているわけではないので、自然に見える角度の正解を今回のケースと比較しているわけではない。blenderの操作方法を覚えていずれは正確に比較してみたい。
たとえばこんなかんじで遊ぶこともできる。
どんな複雑な形もベースは直線と曲線なので、ほとんどの形の「あたり(下書き、位置確認)」として応用がきく。
参考文献
初心者でもわかりやすい本
ロビー・リー「超入門 マンガと図解でわかる! パース教室」
・パース全般の基礎において一冊目にこれを手に取るのに適している。 ・私は「パース!マンガでわかる遠近法」よりも平易に、かつ丁寧に説明されていると感じた。それゆえに、初心者は特に一冊目にこの本をおすすめする。
デヴィッド・チェルシー「パース!マンガでわかる遠近法
・イラストが多く、わかりやすい。パースの基礎用語の説明もされていて、かつ平易にパースの使い方が説明されている良本。ただし、建築パースに特化しているわけではなく、「イラストレーション(漫画)」に特化している点を注意する必要がある。 ・パース全般の基礎を学ぶという目的において一冊目にこれを手に取るのに適している。
上級者向け
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
絵を描く、特に線画に特化した本。小難しいが広く、深く説明されている良本。
山城義彦「現代パースの基本と実際」
・パースの歴史や細かい用語が説明されていて便利。ただしメインはイラストレーションではなく「建築パース」に特化している点を注意する必要がある。 ・かなり小難しく説明されている(建築パースゆえにそうならざるをえないのだろう)。例えるなら文系が理系の数学を見たときのあの感覚に近い。建築家ならば通らなければならない道ではある。ただし、この本はだいぶ古く、現代ではコンピューターグラフィックスをもっと多用して楽をするのだと感じた。ただし、楽をするにもその原理を知っておいて損はない。
その他
参考サイト:パースフリークス(URL)
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
・全般的な絵の知識が語られている本であり、パースに割かれる箇所は少ない。ただし、それなりにそれぞれ濃く説明されている本である。 ・パースを学ぼうとしてとる本ではないが、絵の描き方を学ぼうとする場合は選択肢に入ってくる。ただし高いのが難点。
コメント
この記事へのトラックバックはありません。


































この記事へのコメントはありません。