目次
はじめに
動画での説明
・この記事の「概要・要約」はyoutubeの動画の冒頭にありますのでぜひ参照してください。
よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m
二点透視図法とはなにか、意味、定義、わかりやすく解説
二点透視図法:左右の2つの消失点を使う線遠近法のこと
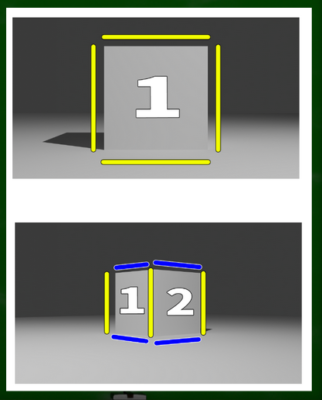
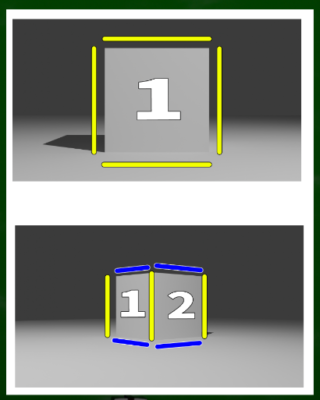
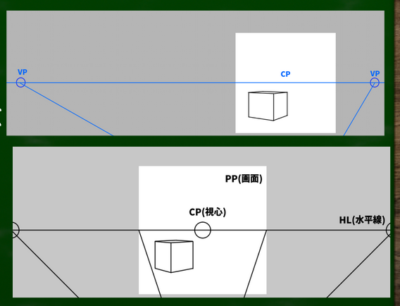
例えば上の景色は一点透視図法であり、下の景色は二点透視図法である。これは同じ立方体を違う角度から見たものである。
では、この2つの「違い」はどこにあるのだろうか。その「違い」を理解することが二点透視図法を理解することであり、この動画の主な目的である。まずは客観的に理解できる「違い」を端的に挙げていき、最後にその理由の解釈を行いたい。
画面の中心にある立方体は何面見えているか?
一点透視図法では視心に「1面」しか見えていない。そして、二点透視図法では「2面」見えている。まずはこの点が両者の違いである。
画面の中心にある立方体の斜線の数、および垂直線、水平線の数は何本か
一点透視図法の場合、水平線(HLと区別すれば、横線)が二本、垂直線(縦線)が二本。二点透視図法の場合、垂直線が三本、斜線が四本。より単純化すれば、一点透視図法は水平線と垂直線から構成され、二点透視図法は垂直線と斜線から構成されている。
カメラや人間の頭はどうなっているか
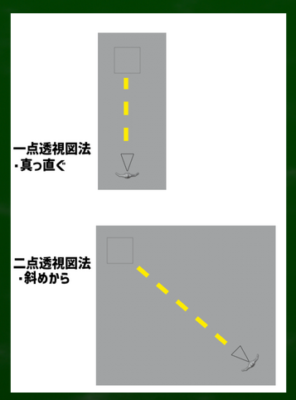
・真上から見たケース
一点透視図法の場合は「真っ直ぐ正面に」対象へ向かっている。二点透視図法の場合は「斜めに」対象へ向かっている。
頭を傾けるとどうなる?
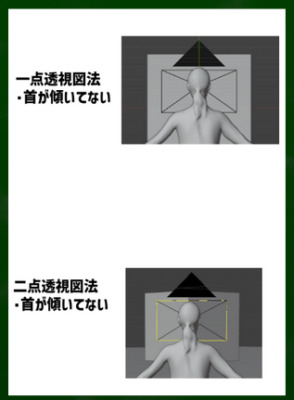
一点透視図法も二点透視図法も、どちらも線は90度に真っ直ぐ伸びていた。
線が真っ直ぐ伸びるということは、首を上下に動かさずに、固定しているということである。では、頭を上下に傾けるとどうなるのか。
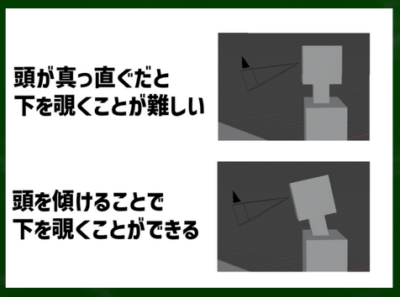
「頭を傾ける」とは上下に首を動かすイメージになる。
たとえば首が真っ直ぐではこのようなカメラを覗くことは難しい。したがって、頭を傾ける必要がある。首を曲げるともいってもいい。※もちろん体ごと、宇宙にいるように斜めにすれば下を覗くことができるが、例外とする。
頭を傾けた場合の景色の1つがこのようなケースである。いわゆる三点透視図法のケースに該当する。ただし、今回は三点透視図法を扱わない。
「一点透視図法と二点透視図法が共に頭を上下に傾けないで真っ直ぐ見ている景色」であることを頭に入れておく。
集束と垂線の関係
収束する線と収束しない線
先ほど、一点透視図法と二点透視図法の垂線、水平線、及び斜線を確認した。
これらは一体何を意味しているのか。
まず、垂線や水平線は基本的に「消失点へ収束しない線」である。
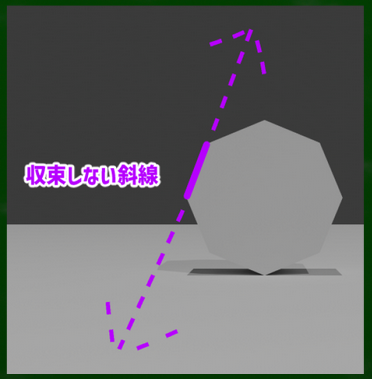
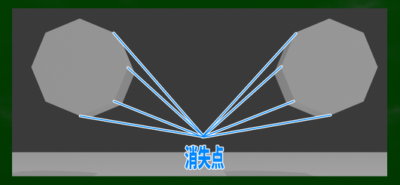
ただし、「斜線だからといって必ずしも消失点へ収束するわけではない」。たとえば右の図のような八角形の前面は斜線だらけだが、その斜線は垂直線や水平線とおなじように、どこへも収束せず、無限に伸びていく。
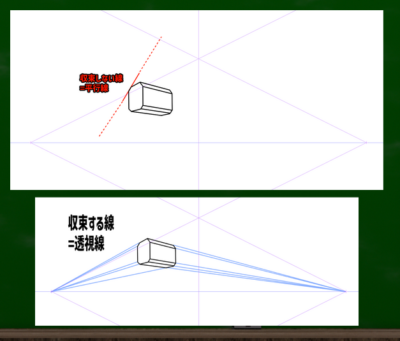
二点透視図法において垂直線や水平線(真横の線)は基本的に「消失点へと収束しない線(非透視直線)」であるが、90度に縦や横に伸びる線(真縦、真横の線)が二点透視図法において存在することを改めて確認する必要がある。
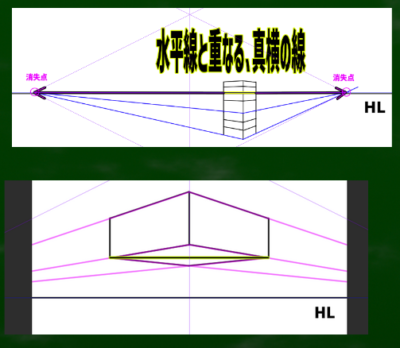
例えば、真横の線は基本的に水平線(たんなる真横の線も、目線の高さにある真横の線も水平線と呼ぶのでややこしい)とちょうど重なる位置で見える(上の図)。ただし、この真横の線は「消失点へと収束する特殊な線(透視直線)」である。真横の非透視直線が存在する場合もあるが、二点透視図法において例外的といえる(下の図)。
透視図法のそれぞれの特徴
ものすごく単純化していえば、以下のようにまとめることができる。
- 一点透視図法では縦と横の線が収束せず、奥行き方向の線だけが消失点に向かう。
- 二点透視図法では縦の線が収束せず、奥行き方向と横方向の線がそれぞれ異なる消失点に収束する。
- 三点透視図法では縦の線も含め、すべての線が消失点に収束する。
ただし、正面の星型や円の斜線や曲線は別に考える必要がある。
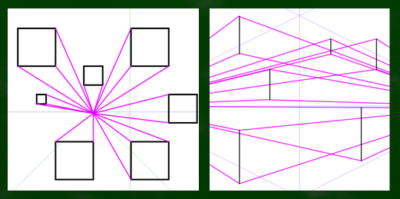
収束する斜線はこちらである。
こちらは一点透視図法の場合であり、「奥行きの線」であるという点がポイントである。一点透視図法の場合、遠近法による収束は奥行方向にしかないからである。つまり、奥行きの斜線は収束する線だというわけである。
二点透視図法、さらには三点透視図法でもこのような斜線はどの消失点にも基本的に収束しない。
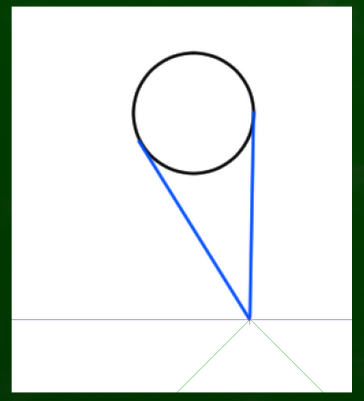
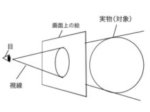
こうした斜線が収束しないのだから、もちろん曲線も収束しない。例えば球体を二点透視図法で描くことは難しい。
もちろん、三点透視図法で描くことも難しい。円を取り入れることは可能だったが、ぎこちない奥行き感しか表現できなかったことを前回学んだ。
円や星を描いてその奥行きにパースを用いる状況をイメージしてみよう。そもそも最初の円や星はパースによって描かれていない。感覚(もしくは幾何学など)を用いて描くという作業によって可能となっている。
奥行きの線(透視直線)は確かに伸ばすことができるが、伸ばしてから曲線を描く際に困ることになるだろう。
ガイドラインとしての二点透視図法
もちろん、ガイドライン的、つまり「アタリ(ざっくりとしたサイズ感、奥行き感)」として透視図法を使うという方法は可能である。さらに、円をうまく描くためのガイドラインとして特化したパースの説明もよくある。
ただし、厳密な球体を二次元の絵を描く際に厳密なパースのもとで表現したいのなら、3Dソフトを使ったほうが望ましい。たとえば工業製品などはそうしたソフトが必要とされ、もしアナログでも幾何学的な知識が必要となるだろう。
アナログでは立方体から自分の力で球体を構成できるような「画力」がそもそも必要になる。基本的に初心者の段階ではまずは立方体を一から三点の透視図法で構成できることを目指すことが望ましいと言える。
場合によっては、この段階で終わってもいいほどのゴールだろう。なぜなら、画力があれば立方体のサイズ感や奥行き感から球体を構成し、さらにその球体から顔を構成することが可能になるからである。描きたいものを全てパースで厳密に描くというのはあまり得策ではない。建築でパースが必要とされるのは曲線のものが少ないからだろう。いずれにせよ建築では専用のソフトがあり、絵を描く場合とは少し異なるケースであると言える。
二点透視図法の種類について
二点透視図法の種類はたくさんある
二点透視図法の種類はいくつあるか。答えは「たくさん」である。
左右の消失点の位置や、目の高さによって何通りにも二点透視図法が作成できることになる。例えば左右に45度の二点透視図法、左に30度、右に60度の二点透視図法では種類が違う。左右に45度で目の高さが50センチと60センチでも種類(見える景色)が違う。
もっとも、無限のように多くあるとはいってもいくつかのタイプに類別することは可能だろう。
たとえば自然な視円錐内に収める必要があるという点で、自然な二点透視図法と不自然な二点透視図法の2つのタイプに分けることができる。
そして自然な、歪みが生じにくい二点透視図法は画面内の視円錐が60度以内だということを前回学んだ。
消失点は基本的に画面外に存在し、その位置が90度視円錐上(視円錐の左右の端)にあるか、それ以外の角度の位置にあるかで区別することができる。
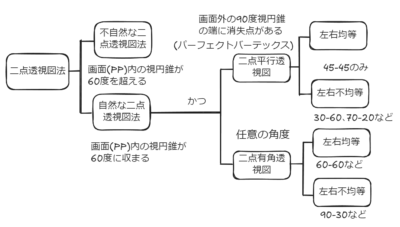
整理するとこのような図になる。※視円錐については以前の動画を参照してほしい。
パーフェクトバーテックスとはなにか、意味、定義、わかりやすく解説
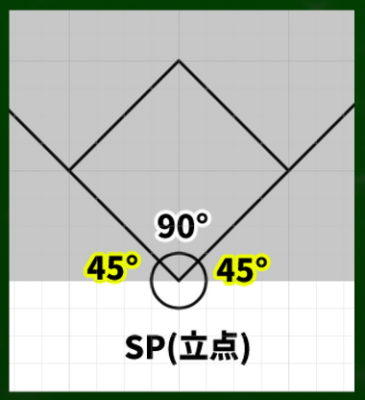
まず、代表的な二点透視図法は45度消失点を用いた「二点平行透視図」である。ロビー・リーがいうところの「パーフェクトバーテックス」にあたる透視図法である。作図しやすいから利用されることが多いのだろう。
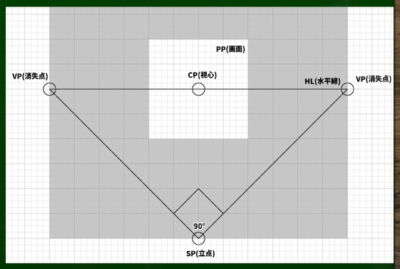
パーフェクトバーテックス(完全な頂点):視心の下にあり、90度の角が実際90度で描かれる点。二点透視図法において、2つの消失点が左右対称な位置関係にある場合、パーフェクトバーテックスも2つの消失点も、視心から等距離にある
立点(SP)から左右の消失点へと線を伸ばしていき、その3点が「直角三角形」を構成するイメージである。
3つの内角のうち1つが90度である三角形が直角三角形である。
45度と呼ぶことができる理由は、「対角線の消失点がそれぞれ、立点から45度の位置にあるから」である。
なかなかわかりにくいが、要するに、消失点へ伸びる直線の角度が45度だという話である。※三角形の内角の和は180度であり、(180-90)/2=45ということになる(分度器をイメージしてもいい)。
自然な画面と、90度視円錐との関係
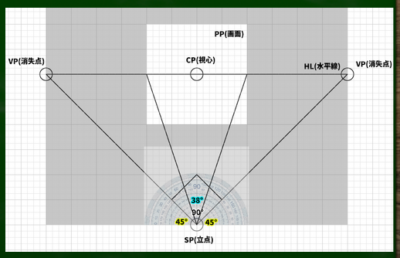
45度だからといって、任意の画面内の視円錐が45度に収まっているということを必ずしも意味していないという点は注意である。
たとえば右の図の画面の場合はおよそ38度の視円錐となる。ここで重要なのは「画面がいかなる視円錐に収まるか」ではなく「消失点がSPから見ていかなる角度にあるか」である。※前者については以前の動画を参照
非均等な直角三角形のケース
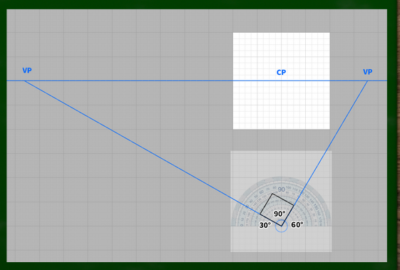
さらに、左右に均等なケースと、非均等なケースが存在する。
たとえば左に30度、右に60度のように左右非対称、非均等にしても「直角三角形」は成り立つ。直角の三角定規があればアナログでも作成しやすい点がポイントだろう(左右対称の場合は三角定規がなくても可能)。
それぞれの正方形の見え方の違いはこのようになる。どのような「見せ方(魅せ方)」をしたいかの選択がクリエイターの腕にかかっているというわけである。
絵のセンスとパースの関係
歪んでいる、歪んでいないといった指標はこの次元では明確にはなく、「センス」が試される領域なのかもしれない。
たとえば写真家が撮る写真はそのほとんどが歪んでいない(カメラが自然に歪まないように調整してくれる)が、美しい写真と醜い写真があることと似ている。ある意味では「構図」の問題と関連する。どういう構図にするべきかは目的による。たとえば「山の雄大さを表現したいという目的ゆえに、下から覗いた感じの構図にする」というような、多種多様なケースが考えられる。
二点透視図法のメリット・デメリット
二点透視図法のメリットとはなにか、意味、定義、わかりやすく解説
- 一点透視図法では見えない景色を構成することができる。具体的に言えば、対象を「斜め」から覗くことができる。
- 一点透視図法よりもダイナミックに見える。
- 一点透視図法よりも「線の後退の度合いが緩やか」なので、厳密に描かなくてもそれらしい仕上がりになる
二点透視図法のデメリットとはなにか、意味、定義、わかりやすく解説
- 作図が難しい、面倒
- 一点透視図法では可能だった「正面の強調」ができなくなり、対象がどういう形をしているかわかりにくい
- 一点透視図法は「シンプルでわかりやすい、力強い絵」を表現できるが、二点透視図法は複雑になりがち。
あなたがもしカメラマンならば、なにを見せたいか
大事なのは「あなたがカメラマンだとして、眼の前の対象をどのように鑑賞者に見せたいか」である。
絵を描く場合も「自分の想像上の世界を撮る、切り取る」という点でカメラマンである。
例えばこの単純な立方体を、あなたはどのように見せたいだろうか。その見せ方にはどういう目的があり、どういう効果があるのか。
これがもし人の顔だったら、と応用させて考えていけばもっとわかりやすい。パースの技術は選択肢を与えるだけで、選択の正解を与えるわけではない。
次回の予定
二点透視図法で立方体を作成する方法を学ぶ。
参考文献
初心者でもわかりやすい本
ロビー・リー「超入門 マンガと図解でわかる! パース教室」
・パース全般の基礎において一冊目にこれを手に取るのに適している。 ・私は「パース!マンガでわかる遠近法」よりも平易に、かつ丁寧に説明されていると感じた。それゆえに、初心者は特に一冊目にこの本をおすすめする。
デヴィッド・チェルシー「パース!マンガでわかる遠近法
・イラストが多く、わかりやすい。パースの基礎用語の説明もされていて、かつ平易にパースの使い方が説明されている良本。ただし、建築パースに特化しているわけではなく、「イラストレーション(漫画)」に特化している点を注意する必要がある。 ・パース全般の基礎を学ぶという目的において一冊目にこれを手に取るのに適している。
上級者向け
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
絵を描く、特に線画に特化した本。小難しいが広く、深く説明されている良本。
山城義彦「現代パースの基本と実際」
・パースの歴史や細かい用語が説明されていて便利。ただしメインはイラストレーションではなく「建築パース」に特化している点を注意する必要がある。 ・かなり小難しく説明されている(建築パースゆえにそうならざるをえないのだろう)。例えるなら文系が理系の数学を見たときのあの感覚に近い。建築家ならば通らなければならない道ではある。ただし、この本はだいぶ古く、現代ではコンピューターグラフィックスをもっと多用して楽をするのだと感じた。ただし、楽をするにもその原理を知っておいて損はない。
その他(パースがメインではない本)
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
・全般的な絵の知識が語られている本であり、パースに割かれる箇所は少ない。ただし、それなりにそれぞれ濃く説明されている本である。 ・パースを学ぼうとしてとる本ではないが、絵の描き方を学ぼうとする場合は選択肢に入ってくる。ただし高いのが難点。
コメント
この記事へのトラックバックはありません。
















この記事へのコメントはありません。