はじめに
動画での説明
・この記事の「概要・要約・要旨・まとめ」はyoutubeの動画の冒頭にありますのでぜひ参照してください｡
よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m
一点透視図法とはなにか
一点透視図法とはなにか
一点透視図法とはなにか､意味､定義､わかりやすく解説
一点透視図法：描かれたオブジェクト(対象)が一つの消失点に向かって収束するパースの技法のこと｡
消失点：線遠近法で､画面の奥へ向かう平行線が収束する点のこと｡
例えばこの線路の写真は一点透視図法のイメージに近い｡
ひとつの消失点へむかって線路(実際には真っ直ぐな線)が曲がって伸びていっている｡
初心者がぶつかる疑問
「なんだ､一点透視図法は簡単じゃないか」と思うかもしれない｡しかし､よくよく考えれば分からないことが多い｡
たとえば「対象物が肩に対してまっすぐ正面を向いている」､「一組の線だけが交差する」､「一点透視図法は､サイズが変わるだけで収束しない箇所がある」など初心者にとっては分かりにくいポイントがたくさんある｡今回はそうした疑問を同じ初心者として解消していきたいと思う｡
対象物が肩に対してまっすぐ正面を向いている
パースにおける肩とは？
まず､ここでいう肩とはもちろん「人間の肩」である｡もちろんロボットの肩でもいいが､とりあえず人間としておく｡そして対象物(オブジェクト)とは､自分が見える景色､描きたい物のことである｡
たとえば立方体がこのように､目の前にあると仮定してみよう｡
この景色を人間が見ていると仮定して､肩はどのようになっているのか｡
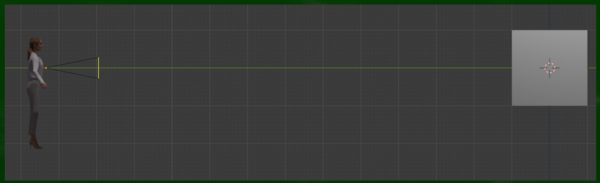
これはblenderソフトなので､人間ではなく「カメラ」が視点となっている｡もし横から撮影画面を見るとこのようになる｡
カメラの位置と人間の肩を重ねてみると､このようになる(厳密には目の位置にくるが､今回は肩と合わせておく)｡
要するに､人間の肩は「水平さ(真横の線)」を表現しているのである｡
四角いカメラの「水平さ」も人間の肩の「水平さ」も同じような表現だと言える｡
こうして「対象物が肩に対してまっすぐ正面を向いている」という一点透視図法の説明が少し理解できるようになる｡
対象物が立方体の場合はさらにわかりやすい｡要するに､対象物のある面の平行さと､観察者の肩の平行さあるいはカメラの平行さ､つまり線の角度が一致するということである｡
一点透視図法における肩と対象の線の角度の一致の例
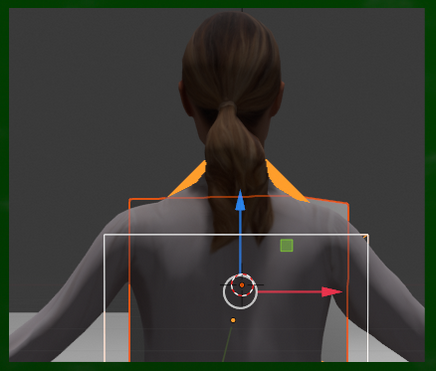
図にするとこのようになる｡
観察者が見ている立方体の水平線と､肩の水平線の角度が一致している｡
一点透視図法における肩と対象の線の角度の不一致の例
では､一致しないケースとはどういう場合か｡
たとえばこのようなケースである｡この画面はいわゆる「二点透視図法」の形式である｡
先ほどと違い､我々に見える対象物の面が同じ角度の平行ではない｡
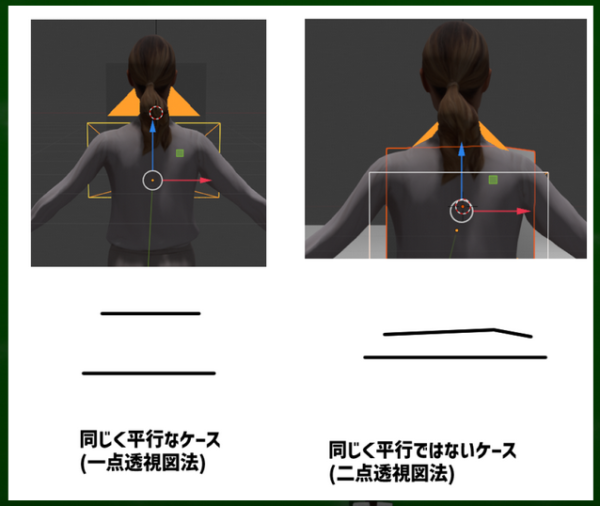
よりわかりやすいように比較の図をつくると､このようになる｡
一点透視図法では常に「対象物が肩に対してまっすぐ正面を向いている」という点がこれで理解できたと思う｡
逆にいえば､「まっすぐ正面を向いていないような形式を構成することはできない」ということになる｡二点透視図法は左右に自由がさらにきくようになり､三点透視図法では更に上下に自由がきくというイメージになる｡
「一点透視図法における斜線」の謎
一点透視図法における斜線､および垂線の例
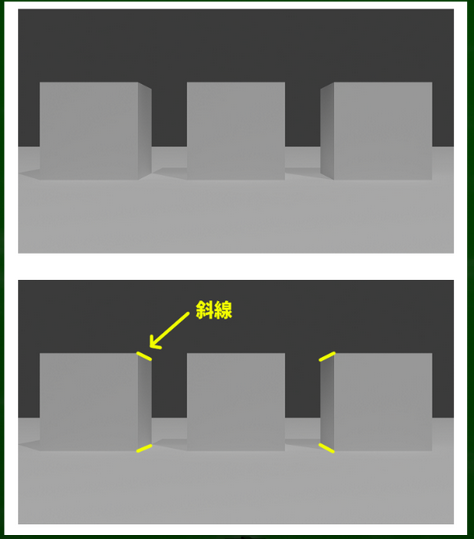
たとえば先程の画面２つの立方体を左右に並べてみると､斜線が見えてくる｡
この斜線は「対象物が肩に対してまっすぐ正面を向いている」という説明とは一致しないように見える｡
図にするとこのようなイメージとなる｡
大事なのは､一点透視図法にも斜線は登場するということであり､全てが肩と同じ角度の水平線ではないという点である｡こんなことは当たり前だと思うかもしれないが､その意味をよく理解できていない場合がある｡
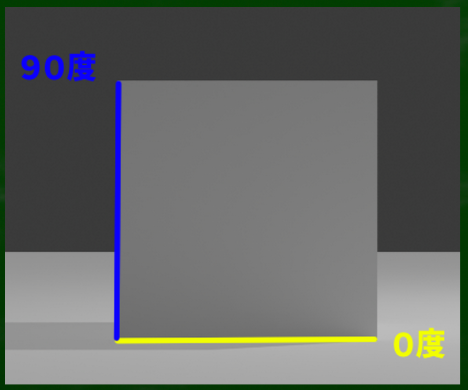
そもそも正面ですら､水平線ではない線がある｡つまり､「垂線」が存在する｡
縦に伸びる線であり､これは肩の水平線と同じ角度ではない｡言い換えれば､０度ではなく９０度の線がある｡
一点透視図法は「あるひとつの線が､肩と同じ角度である」という点を理解すれば､他の線が違う角度であっても納得はいく｡
さきほどの３つの立方体も､ある側面では必ず同じ角度の線があった｡
「正面になるように立方体を配置する」とは
立方体をどこに配置しようとも､必ずある線は肩と平行ということになる｡
重要な点は､「正面になるように立方体を配置する」という点であり､「視点(人間やカメラ)の方に立方体が向いている」ということではない｡
もちろん､人間の真正面､画面の中心にある立方体は必ず視点を向いている必要があるが､それ以外はそうではない｡一点透視図法の画面の中央の対象物には奥行きがないという点もポイントだろう(斜線､収束する線がない)｡
適切に立方体を配置すると､必ず肩と平行な線が生じる｡
「適切に」とは単に正面を向くように立方体を適当に置いただけである｡
立方体における正面､あるいは前面､表とは？
しかしどこが前面(正面)で､どこが前面ではないのか､謎である｡たとえばカードゲームのカードには裏と表があり､絵が描いてあるほうが表で､前面である｡
しかし何も描かれていない白紙のカードではどちらも意味的には前面(表)になりうる｡大事なのは我々側が前面・後面を意味づけるのではなく､「単に肩と平行であるという事実が前面を表している」という点である｡立方体の場合は「肩と平行でなければ､前面以外」である｡たとえばサイコロには１から６の面があるが､どの面であっても肩と平行な線が見えれば､それは前面として扱う｡
たとえば前面ではないケースはこのような配置である｡このケースでは「一点透視図法と二点透視図法が混在している」ということになる｡
自然な人間の視点は三点透視図法？
通常の人間の視点は一点透視図法でも二点透視図法でもなく､どちらかといえば三点透視図法に近い｡あるいはそれらの混在である｡
しかしこう言われても､頭に疑問が浮かぶばかりなのが､私のような初心者である｡すこし想像してみよう｡机にサイコロが１０個あるとする｡そのサイコロのうち､いくつが正面を向いているだろうか｡
なんらかの偶然で１個か２個､正面を向いているということはありうる｡しかしそのほとんどはどこか斜めを向いているに違いない｡
たとえば一点透視図法のみの世界から､こんな景色が構成されるかもしれない｡要するに､左右にも上下にも自由がないような絵である｡こんな景色は現実ではまず出会わない｡
もし二点透視図法のみの世界で構成するとしたら､こんな画面にすることができる｡しかしどこか､これも不自然だ｡我々は普段､もっとサイコロを見上げたり､見下ろしたりしていないだろうか｡
たとえば三点透視図法のように机の上にあるサイコロを見下ろす場合は､こんな感じになっているかもしれない｡１の面が揃ってしまっているのはすこし不自然だが､それを除けばありうる景色である｡
一点透視図法だけをマスターすればどんな絵も自然に描けるようになる､というわけではないという点を抑えることが重要である｡
現実世界では三点透視図法が近い｡もちろん､電車の線路のように一点透視図法に近い景色もあるが､稀である｡我々が想像によって絵を構成する際に､一点透視図法をなぜ選択するのか､その意図を自分で深く理解しておくことが重要になりそうだ｡
一点透視図法のメリット・デメリット
一点透視図法のメリット
【メリット】簡単に作図することができる｡動きやドラマ性を強調することができる｡
「主題に焦点を当てるシンプルさ」や「奥行きや遠近感の強調という意味でのインパクト」を狙ったものだといえる｡
一点透視図法のデメリット
【デメリット】丸みのある物に使いにくい｡見上げている感じや見下ろしている感じ､斜めから見ている感じを出したいときには使えない｡
構図の自由度が他の透視図法より制限される｡中央の一番見せたい対象に奥行きをつけにくい｡
一点透視図法による効果線
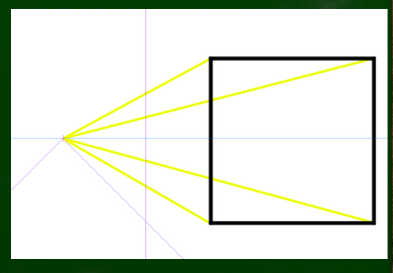
たとえば効果線では一点透視図法の線を利用したものがある｡
消失点が１点だけであり､その一点に集中することにより､鑑賞者はその箇所に注目するという効果を生むのである｡
一点透視図法は「丸みのある物に使うことはできない」？
「丸みのある物に使うことはできない」とはいったいどういうことか｡
一点透視図法は主に直線的な物体の奥行きと遠近感を強調するための技法であり、球体のような曲線的な形状には適していないという｡三点透視図法など､もっと複雑な透視図法を使う必要がある｡
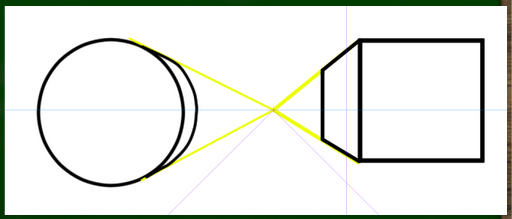
例えば円にこのように奥行きをつけても､我々が思い描くような球体にはならない｡ロビー・リーの言葉で言えば「かっちりした輪郭ができて別なものになってしまう」のである｡
その点､直線からのみできている立方体にはその心配が少ない｡
一点透視図法は何から何まで直線(九〇度や〇度の線)で正面を構成するわけではない
また､一点透視図法であったとしても「何から何まで直線(縦・横)で正面を構成する」わけではない｡
あえて斜線で正面を構成するテクニックもある｡かっちりした角ではなく､斜線にしたり丸みを帯びたオブジェクトにしてもいい｡ただし､奥行きは輪郭的になってしまう点を考慮する必要がある｡
たとえばこの星型には､どこにも肩と平行な線がないように見える(それっぽい線もあるが､厳密には全て斜線である)｡
しかし､どの星型も正面を向いている｡
「オブジェクトが正面を向いているかどうか」が重要であり､「オブジェクトが視点を向いてるかどうか」ではない
重要なのはオブジェクトが正面を向いているかどうかであり､自分の肩と同じ角度の平行線が見えるかどうかではない｡
たとえば右側の立方体は自分の肩に向いていないが､自分の方と同じように平行であるという点がポイントである｡左側の立方体は自分の肩に向いているが､平行ではない｡
一点透視図法のみでは不自然な絵が構成されるケース？
たとえば平行線がない星型のオブジェクトに奥行きをもたせようとすると､このようになる｡
斜線や丸みを多用して星を構成することもできるが､その場合は一点透視図法だけでは難しい｡他の透視図法も併用する必要がある｡
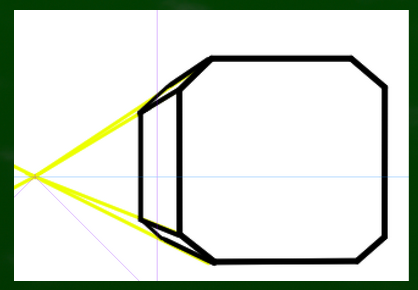
たとえばこのような丸みのある星は一点透視図法のみでは厳密に構成することが難しい｡
あらゆる透視図法がもつ限界と効率
そもそもの話､丸みを帯びた､直線的ではないものをパースで厳密に構成することはどの透視図法でも難しいといえる｡これは一点透視図法だけの問題ではない｡
パースのみで全てを１から１００まで完成させようとするのではなく､おおよそのサイズ感や立体感を把握するためにパースをアタリ(目安)として､下書きとして利用することが懸命ではないだろうか｡
そうした意味ではすべてを立方体的に把握して､その場のサイズ感を知ることはとても有用になる｡
立方体的に把握するだけならば一点透視図法も､二点透視図法も､そして三点透視図法もさほど難しくはない｡もし球体のサイズ感を､事細かく知りたい場合は､いっそのこと３Dで作成してサイズ感をつくるのもありなのかもしれない｡逐一､アナログやデジタルのパースで球体的な下書きをつくることは私には今のところ賢明には見えない｡一部の職人的な作業に携わる人達に必要なテクニックなのではないだろうか｡
次回の予定
次回は一点透視図法で立方体を構成する方法について説明する予定｡たとえばこのように前面を描いたとして､どこまで奥行きを設定すればいいのか､という問題に取り組む｡いわゆる「対角線の消失点」の問題である｡
参考文献
初心者でもわかりやすい本
ロビー・リー「超入門 マンガと図解でわかる! パース教室」
・パース全般の基礎において一冊目にこれを手に取るのに適している｡ ・私は「パース！マンガでわかる遠近法」よりも平易に､かつ丁寧に説明されていると感じた｡それゆえに､初心者は特に一冊目にこの本をおすすめする｡
デヴィッド・チェルシー「パース！マンガでわかる遠近法
・イラストが多く､わかりやすい｡パースの基礎用語の説明もされていて､かつ平易にパースの使い方が説明されている良本｡ただし､建築パースに特化しているわけではなく､「イラストレーション(漫画)」に特化している点を注意する必要がある｡ ・パース全般の基礎を学ぶという目的において一冊目にこれを手に取るのに適している｡
上級者向け
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
絵を描く､特に線画に特化した本｡小難しいが広く､深く説明されている良本｡
山城義彦「現代パースの基本と実際」
・パースの歴史や細かい用語が説明されていて便利｡ただしメインはイラストレーションではなく「建築パース」に特化している点を注意する必要がある｡ ・かなり小難しく説明されている(建築パースゆえにそうならざるをえないのだろう)｡例えるなら文系が理系の数学を見たときのあの感覚に近い｡建築家ならば通らなければならない道ではある｡ただし､この本はだいぶ古く､現代ではコンピューターグラフィックスをもっと多用して楽をするのだと感じた｡ただし､楽をするにもその原理を知っておいて損はない｡
その他(パースがメインではない本)
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
・全般的な絵の知識が語られている本であり､パースに割かれる箇所は少ない｡ただし､それなりにそれぞれ濃く説明されている本である｡ ・パースを学ぼうとしてとる本ではないが､絵の描き方を学ぼうとする場合は選択肢に入ってくる｡ただし高いのが難点｡
コメント