目次
はじめに
動画での説明
・この記事の「概要・要約」はyoutubeの動画の冒頭にありますのでぜひ参照してください。
よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m
2次元曲線とはなにか、意味、定義、わかりやすく解説
2次元曲線:最大次元数が2の曲線のこと。主に、幅と高さの2次元であり、奥行がない曲線を意味する。
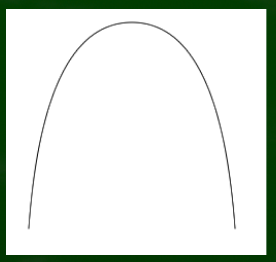
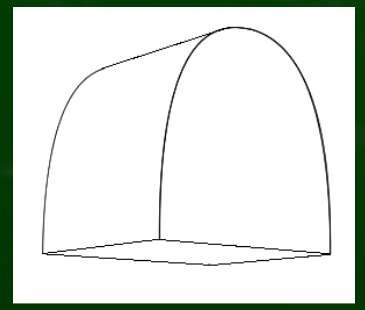
たとえばこのような描画は奥行きが表現されていないので、2次元曲線である。
いわゆる平面図などで主に用いられる図形である。一点透視図法の正面の場合も、2次元曲線的であるといえる。
パースで奥行を表現する場合、3次元曲線となる。
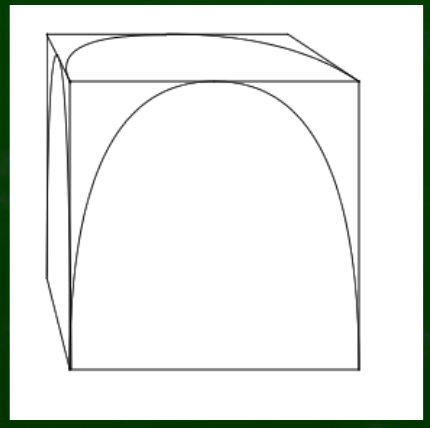
この画面は一点透視図法なので、正面が2次元曲線的であり、側面は3次元曲線的であるといえる。もっとも、ディスプレイに映っている画像は2次元のものであり、奥行があるように見せかけているにすぎない(例えばぬいぐるみの画像がどんなにリアルに見えてもつかむことはできない)。
平面図における2次元曲線の転写のやり方
例えばこのような2次元曲線をもう片方に転写したい場合、どうすればいいのだろうか。
まずデジタルなら複製したあとに左右を反転するような変形を行えばそれで終わりである。アナログの場合はもう少し工夫する必要がある。
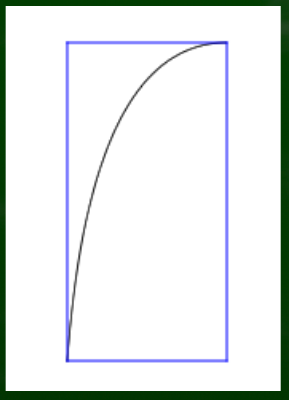
[1]まずは曲線を四角形で囲む
四角形でまるごと囲むとこのようになる。
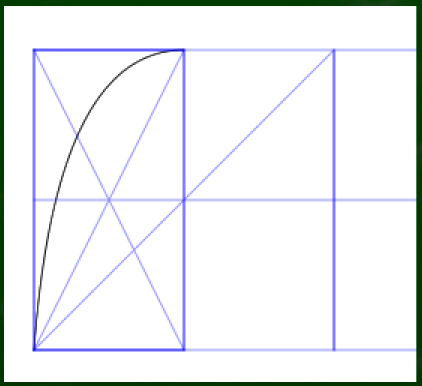
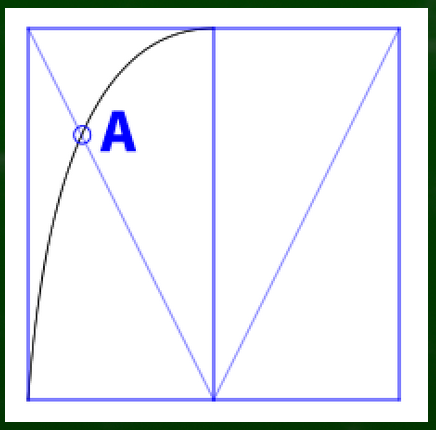
[2]対角線を利用して転写する点を見つける
まずは四角形を複製する。定規で測ってもいいし、対角線を利用して複製することもできる。
対角線と交わる点Aを見つける。
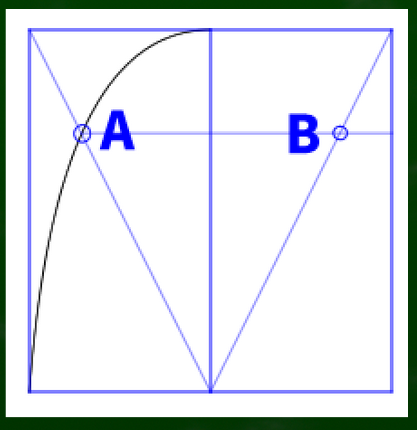
Aから右に直線を引き、対角線と交わる点をBとする。このBが転写された曲線の指標となる。
四角形全体の対角線を引き、曲線と接する点を見つけていく。先ほどと同じ手順で引いていき、交点をC、Dとする。
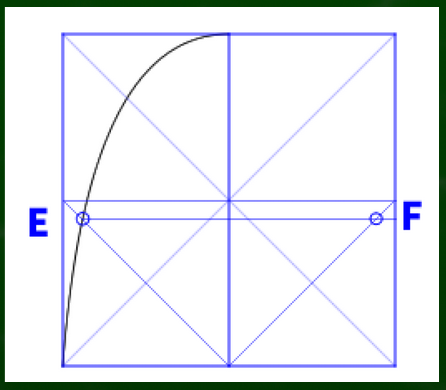
さらに四角形の中心を基準に直線を引き、その端へ下から線を引いていく。この線と曲線が交わる点をE、Fとする。
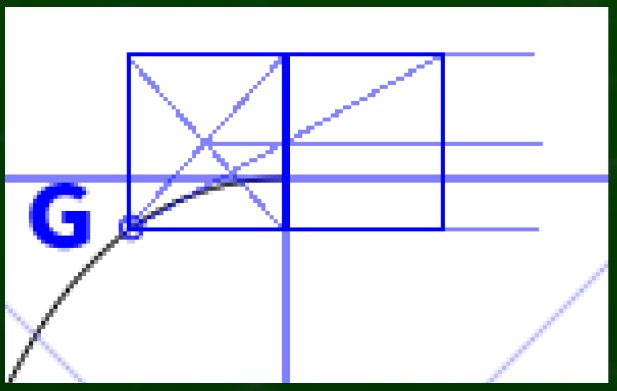
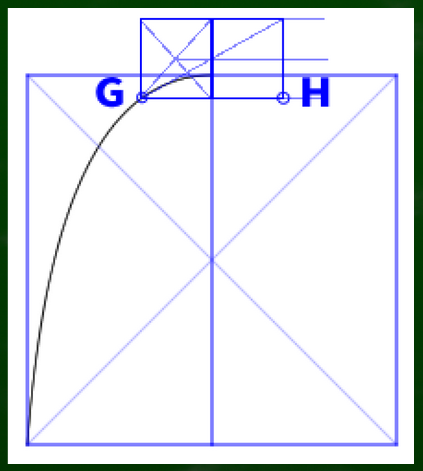
任意の点を転写したいときは四角形を利用する。たとえばこのG点を転写したい場合、このG点を軸に四角形を作る(正方形でなくてもいい)。
高さは任意でいい。
この四角形を右にも複製する。定規で測ってもいいし、対角線を利用してもいい(平面図なので収束せず、実寸の比率となる)。
転写された先にある点がHとなる。
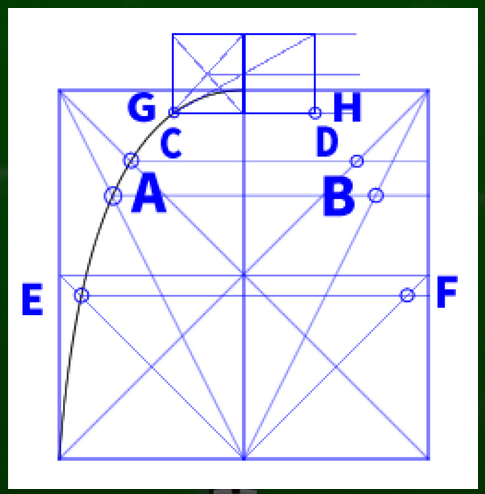
AからHまでの交点をすべて表示するとこのようになる。
任意の点はいくらでも増やすことができる。点が多ければ多いほど指標が多くなるので、フリーハンドで転写しやすくなる。必要な分だけ追加しよう。(この曲線の場合は)4~6個あれば十分だろう。できるだけ均等に配置すると描きやすい。
[3] 指標を参考にしながら曲線を引く
これで2次元曲線の反転描写の完成である。
【tips】曲線を模写する際、どこを指標にするべきか
微分積分を絵描きに役立てる
先ほど任意の(設置しやすい)指標を決めていったが、どういう点を指標にすればいいか困るという問題がある。
数学では微分積分という分野がある。簡単に言えば、曲線を直線的な視点から理解するための数学のことである。私は数学が苦手なので詳しくはないが、しかし絵を描く際に明らかに有用になる知識であり、学ぶ価値があると考える。
曲線を拡大していくと、ある点では直線に(極限的に)近づいていくと考えていくらしい。このときの傾きを求める方法が微分である。今回は難しい話は行わず、ざっくりとこの考えを理解していく。
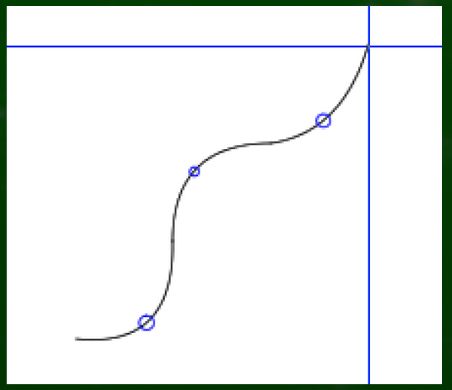
たとえばこのような曲線の場合、直線に近そうな点を見つけていくと、直感的にいえばこの辺りになるだろう。
要するに、カーブしきった凸の一番大きなところ、いわば登りきった山頂(あるいはその逆)は目安にしやすい。
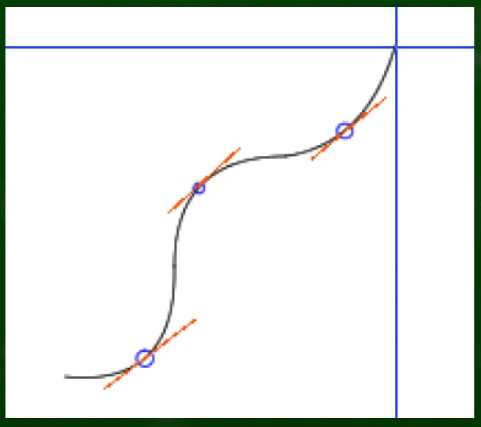
数学的にいえば傾きが0のところとなる。斜線ではなく水平に見えるイメージである。
お気づきの方もいるだろうが、これは模写の際のテクニックにもなる。
画像や写真、現物を参考にして曲線を目の前の紙に目視で写し取るとき、直線に見える指標を把握しておけば転写しやすくなる。
もちろん数学的な計算によって割り出すことも可能かもしれないが、今回は触れない。
微調整的な感覚を学習する
上手い人はこのような理論を意識して使わずとも、テクニックを無意識に使っているのかもしれない。
AとBの線はBとCよりもすこし曲線的、すこし大きい、すこし直線的というような感覚がデッサンによって身についているケースだといえる。そしてこの微調整的な感覚は微積分的な指標の感覚を意識的に身につけることで、学習の速度を高めることが可能になるのではないだろうか。
もちろん、この指標を参考にして反転描写することも可能である。
透視図における2次元曲線の転写
基本的にはさきほどの平面図の2次元曲線と同じ作業を行っていくだけである。ただし、奥へ行けば行くほど短くなるという点を理解しながら線を引く必要がある。
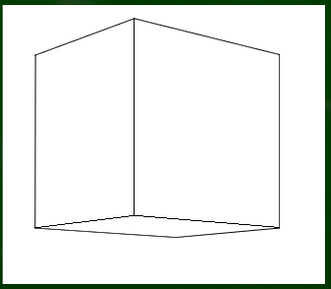
たとえばこのように立方体を構成してみた(二点透視図法における立方体作成方法については第六回の動画を参照)。
【第六回】パース基礎:「二点透視図法で立方体を作成する方法」を解説
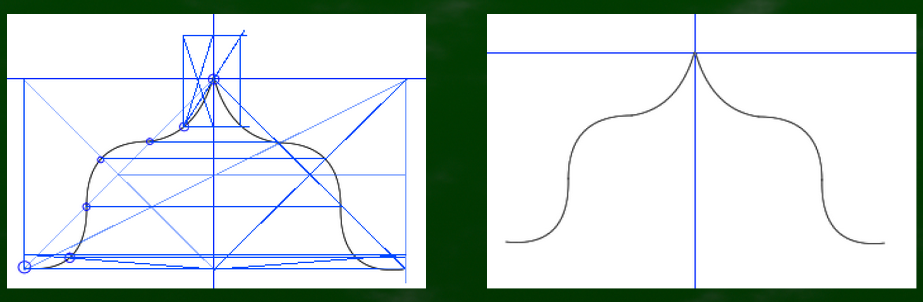
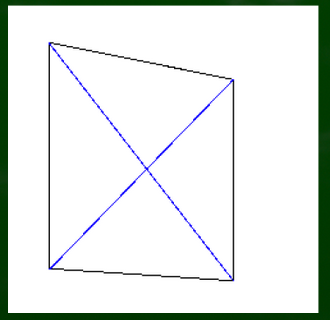
まずは側面に対角線を引き、2分割する。次に、片側に適当に曲線を引く。
この曲線を片側に反転する作業をこれから行う。
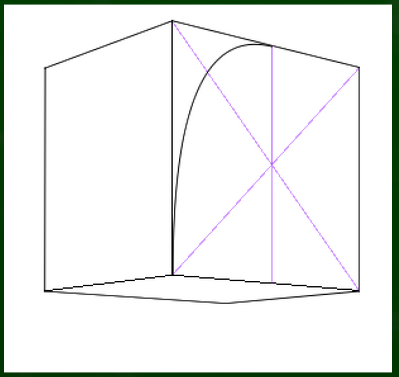
基本プロセスは2分割した際にできた指標をコピーしていくというものである。
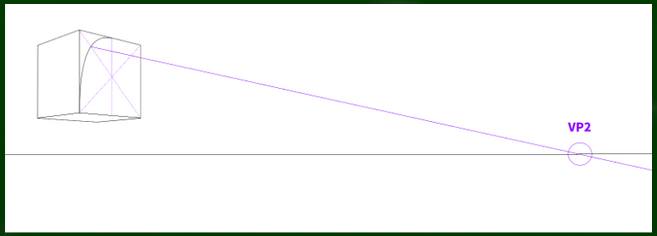
この際、平面図のような真っ直ぐの線ではなく、消失点へむかって収束する線を引いていくことに注意する必要がある。
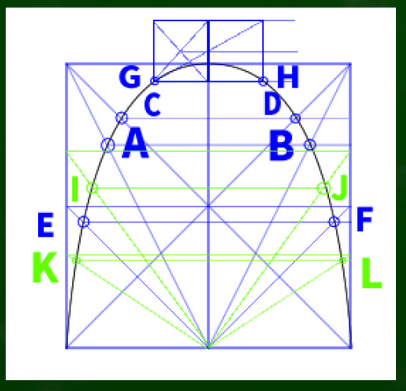
交点をそれぞれA、Bとしておく。
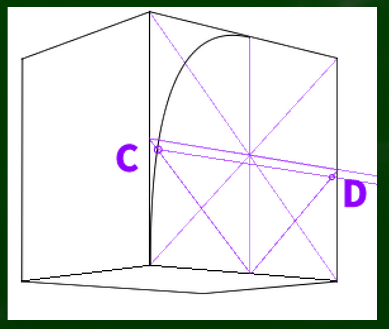
次は中心に線を引き、指標をコピーしていく。この交点をそれぞれC、Dとしておく。
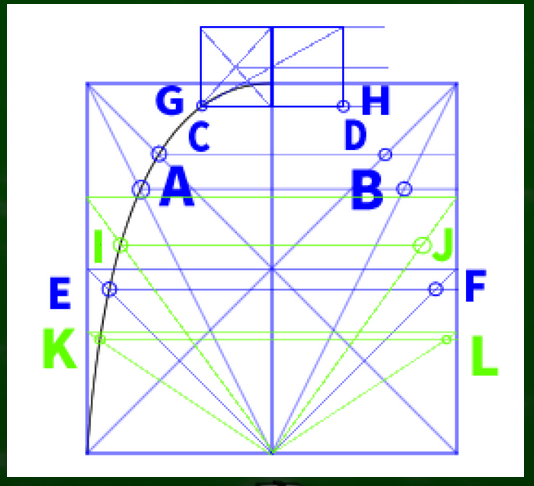
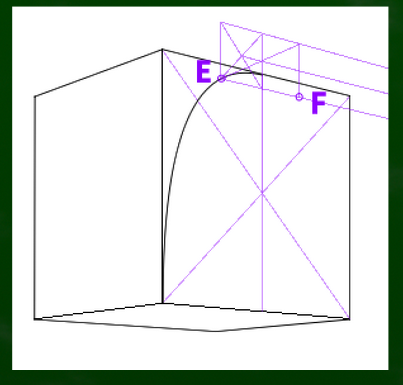
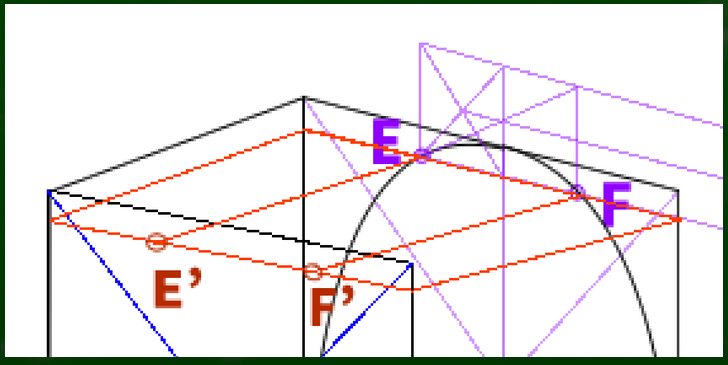
四角形を適当に描いて、E、Fの交点を作っていく。なんとなく盛り上がった箇所をできるだけ指標にしたい。
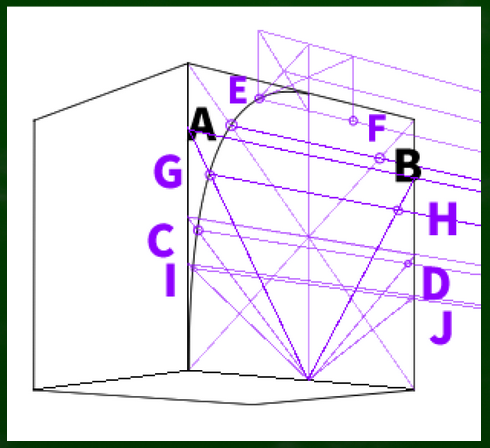
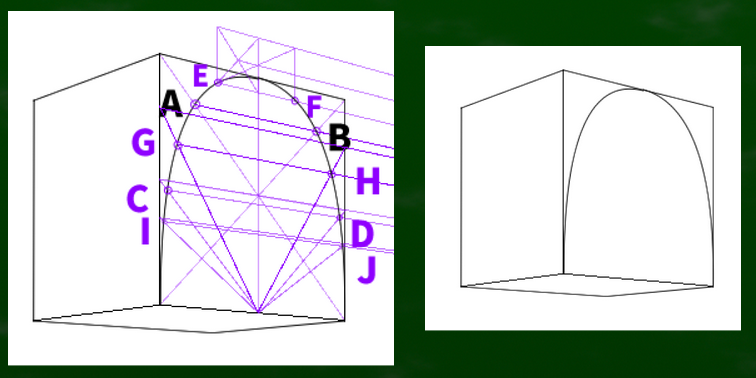
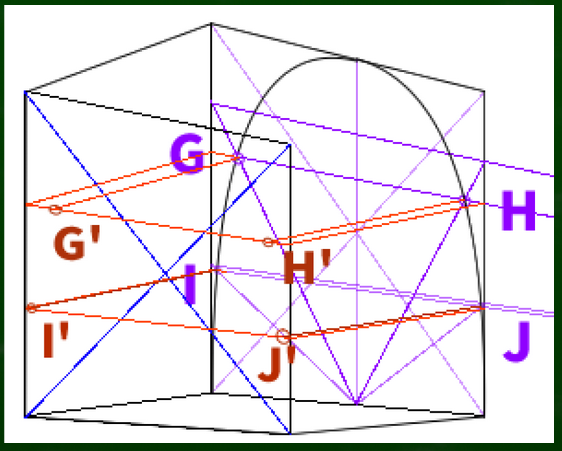
AからFだけでも可能だが、念の為Jまで作ってみた。
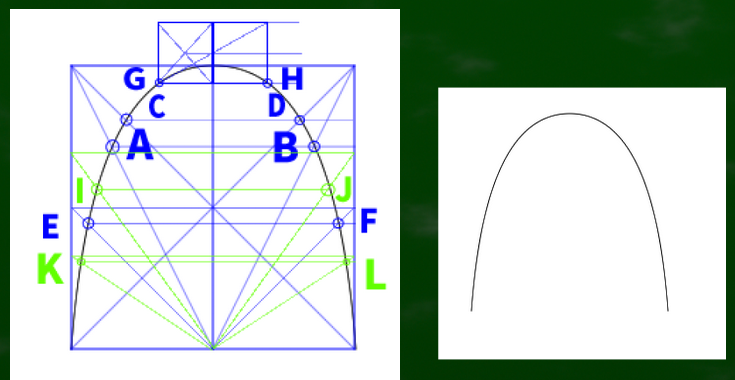
これらの指標を元に曲線を転写すると、このようになる。
【応用】奥に2次元曲線を転写するケース
先程の立方体の奥に曲線を転写するにはどうしたらいいか、考えてみよう。
位置でいうと、この緑の四角形あたりにさきほどの曲線を転写したい。
[1] 対角線を書く
[2] さきほど作った曲線のなかで、対角線と接しているものを探し、奥に線を延長する。
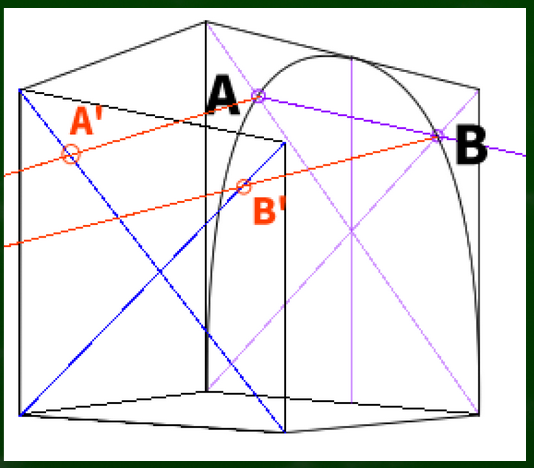
つまり、AとBを奥へと延長させることになる。
AとBを消失点へと伸ばし、奥の対角線と接する点をマークしていく。今回はA’とB’としておく。
[3] 残りも延長させていく
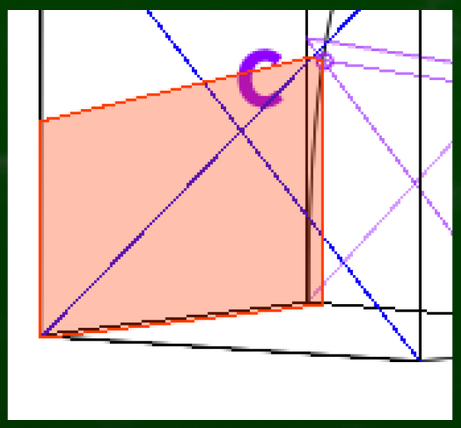
たとえばCから消失点へと線を伸ばし、直方体(赤い部分)を作るイメージになる。
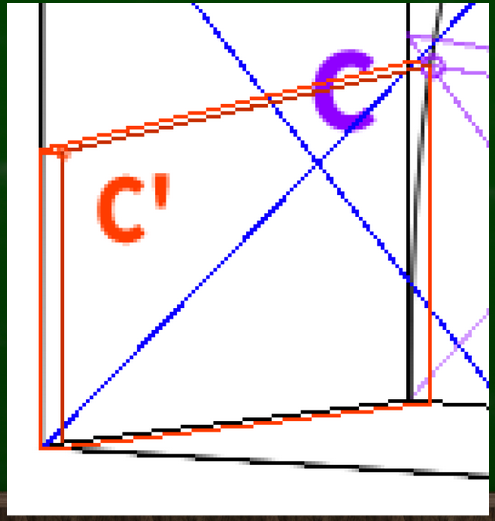
これでC’の位置がわかった。
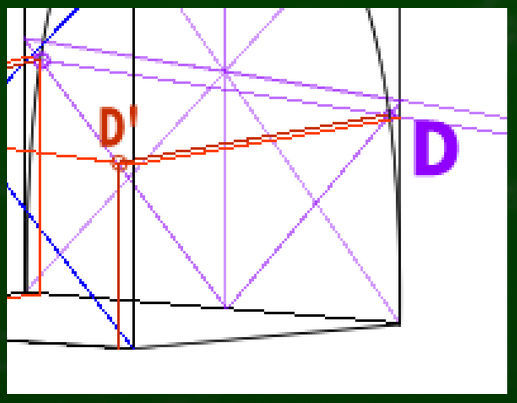
D’の位置も同じように見つけていく。
EFも同じように延長させていく。
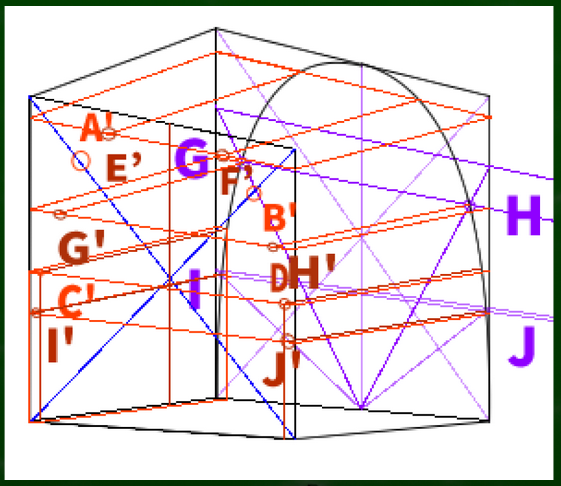
G~Jも同じように延長させる。
すべて表示させるとこのようになる。
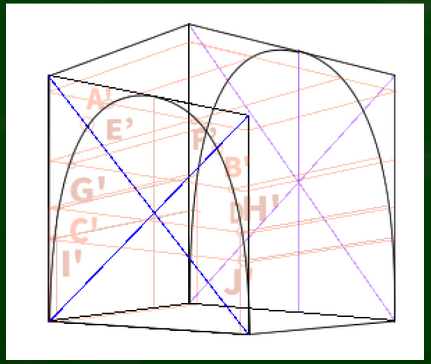
指標を元に、曲線を描いていくと完成である。
たとえばこのような形状を構成することができる。
次回の予定
・(おそらく)パースグリッドについて考察する予定
参考文献
初心者でもわかりやすい本
ロビー・リー「超入門 マンガと図解でわかる! パース教室」
・パース全般の基礎において一冊目にこれを手に取るのに適している。 ・私は「パース!マンガでわかる遠近法」よりも平易に、かつ丁寧に説明されていると感じた。それゆえに、初心者は特に一冊目にこの本をおすすめする。
デヴィッド・チェルシー「パース!マンガでわかる遠近法
・イラストが多く、わかりやすい。パースの基礎用語の説明もされていて、かつ平易にパースの使い方が説明されている良本。ただし、建築パースに特化しているわけではなく、「イラストレーション(漫画)」に特化している点を注意する必要がある。 ・パース全般の基礎を学ぶという目的において一冊目にこれを手に取るのに適している。
上級者向け
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
絵を描く、特に線画に特化した本。小難しいが広く、深く説明されている良本。
山城義彦「現代パースの基本と実際」
・パースの歴史や細かい用語が説明されていて便利。ただしメインはイラストレーションではなく「建築パース」に特化している点を注意する必要がある。 ・かなり小難しく説明されている(建築パースゆえにそうならざるをえないのだろう)。例えるなら文系が理系の数学を見たときのあの感覚に近い。建築家ならば通らなければならない道ではある。ただし、この本はだいぶ古く、現代ではコンピューターグラフィックスをもっと多用して楽をするのだと感じた。ただし、楽をするにもその原理を知っておいて損はない。
その他
参考サイト:パースフリークス(URL)
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
・全般的な絵の知識が語られている本であり、パースに割かれる箇所は少ない。ただし、それなりにそれぞれ濃く説明されている本である。 ・パースを学ぼうとしてとる本ではないが、絵の描き方を学ぼうとする場合は選択肢に入ってくる。ただし高いのが難点。
コメント
この記事へのトラックバックはありません。
















この記事へのコメントはありません。