はじめに
動画での説明
・この記事の「概要・要約」はyoutubeの動画の冒頭にありますのでぜひ参照してください｡
よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m
【前提】はじめに
三点透視図法で正確な立方体をアナログで描くことは難しい
たとえばキャンバスに適当に斜線を引くとする｡三点透視図法において､立方体はすべて斜線であり､垂線や水平線は基本的にない｡では､適当に引いた斜線と実測において同じ長さの残りの斜線を､どうやって引くのか｡
三点透視図法の中でも｢適当な立方体(直方体)を描く｣ケースと､｢立方体を描く｣ケースでは難易度が異なると言える｡
追記(2025/05/08):どうやら立方体と正六面体を混同して､｢正立方体と表記してしまっていたようだ｡そもそも立方体を直方体ないし単なる立体として認識してしまっていたのかもしれない｡正方形で構成される立体が立方体であることを修正しておく｡
たとえばビルや家､人をなんとなくいい感じで三点透視図法っぽく描く､というケースの難易度は低い｡しかし(建築的な意味での)正確な長さで描くというケースは難易度が高い(丸みを帯びた人間を正確な長さで描くのはほとんど不可能なレベルで難しいだろう)｡そもそもそれほどの｢正確さ｣が絵を描く人の全てに求められているかというとそうではない｡また､正確だからといって美しい訳ではない｡しかし正確な絵から美しい絵に崩すことも可能であり､スキルのひとつとして身につけて損はないだろう｡仕事では正確な絵が求められる場合もある(建築家だけではなくデザイナーも求められる)｡
立体感覚を身につけるためにアナログパースを学ぶ
もちろんデジタルならもっと簡単に三点透視図法による立方体を構成できる｡たとえばクリスタにはパース定規があるし､フォトショップにも似たような機能があるだろう｡建築用のPCソフトにはもっと便利な機能が満載されている｡また､仕事の現場ではPCで主に構成するのだと思う｡単に正確な絵を描くという目的を実現したいなら､デジタルの操作方法を学ぶことが合理的であるといえる｡
しかし｢パースの原理を知りたい｣､｢アナログでもなんとか描きたい｣､｢立体的な感覚を身につけたい｣という目的にとって､これらのデジタルソフトの操作方法はあくまでも理解の補助的な位置づけになる｡
【基礎】三角形の垂心とはなにか
絵を描くために幾何学の知識が必要
まずは三点透視図法を学ぶ際に最低限必要になるのが｢幾何学の知識｣だ｡
文系であるわたしは幾何学の知識に乏しい｡ある種の｢壁｣がここにはある｡この壁を見て引き返す人が絵描きの中には多いかもしれない｡人は理解できないものに長時間接していられない｡ただ面倒なだけではなく､そもそも理解できないからパースを避ける｡
絵を描くために幾何学の知識は必須ではないが､しかし絵の技量を高めるために幾何学の知識はなんらかのプラスになると信じている｡
とはいっても今回は難解な幾何学ではなく､小学生の頃に学んでいそうな幾何学なので心配はしないでほしい｡
三角形の垂心の定理とはなにか､意味､定義､わかりやすく解説
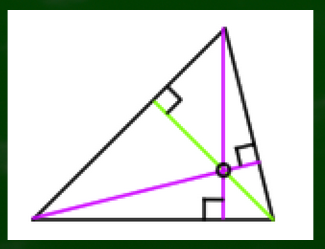
三角形の垂心の定理：三角形の三つの各頂点から対辺(またはその延長)に下ろした垂線が一点で交わること｡この交点を｢垂心｣という｡
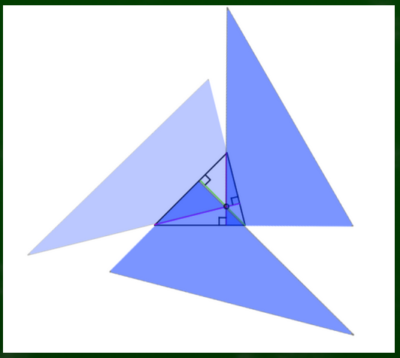
図で言えばこのようなイメージとなる｡三つの各頂点から対辺におろした垂線の角度は｢90度｣になる｡
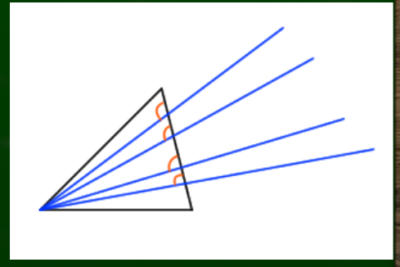
ただ真っ直ぐの線なら直線定規でも引けるが､しかし直線定規で引かれた線が90度(直角)である保証はない｡
ここでいう90度とは相対的なものであり､ある辺に対して90度であるかどうかという点がポイントになるからだ｡たとえば上の図の青い線はどれも直線ではあるが､(相対的に)90度の線であるとはいえない｡垂心を求める場合は基本的に90度になる線は各頂点から一本だけだといえる｡
｢各頂点から対辺に真っ直ぐ線を下ろす｣方法
ここで文系のわたしは､｢各頂点から対辺に真っ直ぐ線を下ろす｣という文章を正直よく理解できない｡どうやったらうまく真っ直ぐ引けるのだろうか｡
コンパスを使う方法と三角定規を使う方法があるらしい｡コンパスは紙に穴が空くタイプのものが多そうなのでパスする(穴が開かないものもあるが)｡今回は三角定規(直角定規)を使う｡分度器を使ってもいいかもしれない｡しかしコンパスのほうがなにかと便利である｡コンパスは三点透視図法の作図全般で､特に円を描く際に必要になる｡
この青い三角形が三角定規だとすれば､このようにぴったり合わせることで垂線をきれいに引くことができそうだ｡
直角三角形がない場合は､直線定規を２つ利用するといいかもしれない｡それすらない場合は､紙を折って作ったり､本を２つ使ったりと工夫することができるだろう｡
残りも同じように引くことができる｡
後で必要になるので､３つとも引いておいたほうがいい(垂心自体は２つ引けば求めることができる)｡
垂心と三点透視図法の関係
垂心がわかったところで､三点透視図法にどのように関係するのか｡
三点透視図法における3つの消失点は｢三角形｣を構成することになる｡この三角形の中心が画面の中心となる｡したがって､｢垂心の位置が画面の中心(CP､VC)となる｣というわけである(もちろん､完成した絵の中心が必ずしも垂心である必要はないのだが､そのほうがバランスがとれる)｡
では次に､どのような三角形の形状が好ましいのか､三角形と画面はどのような関係が好ましいのかという問題が生じることになる｡
今回は作図が簡単な｢正三角形｣のケースを基本として扱う｡慣れれば簡単に作成できるが､しかし｢自分が描きたい角度であるとは限らない｣という点が問題となる｡カメラで景色を撮るときに､どんな角度からとるか悩んで対象の美しさを引き出すことがあるように､三点透視図法の三角形の形も悩む必要がある(細かく言えば何億､何兆通りもあるが､しかし実際に使用する角度はそこまで多くないだろう)｡
しかし正三角形以外はかなり構成が難しく､煩雑であるという点がやっかいだ｡ただし､後述するように､一度作ってしまえば使い回しがきくので､やればやるほどレパートリーが増えて楽になっていくといえる｡
また､この角度いいなとおもった写真やイラストを参考にしながら美しい三点透視図法を設定するといったことも可能である｡
【基礎】正三角形の三点透視図法で立方体をつくる
正三角形を構成する方法
正三角形：3辺の長さおよび三つの内角の等しい三角形のこと｡基本的にそれぞれの角度は60度になる｡
正三角形の高さを見つける
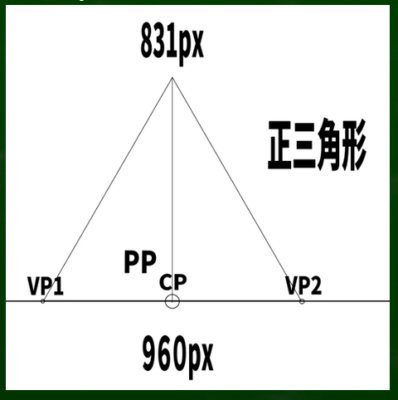
仮に２つの消失点がこのようにあるとすると､もう一つの消失点(上下どちらか)はどのように決まるのか｡
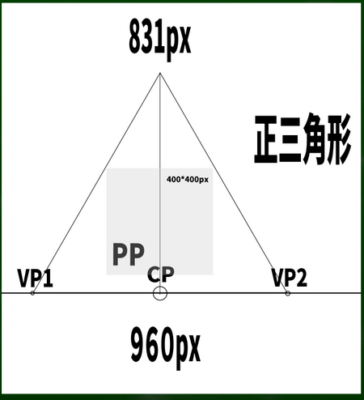
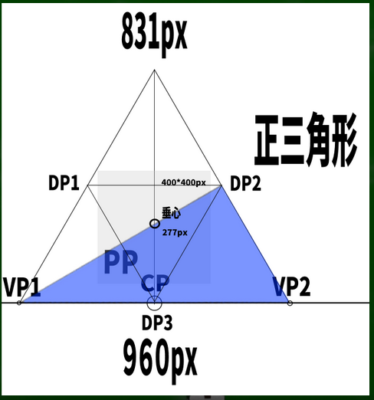
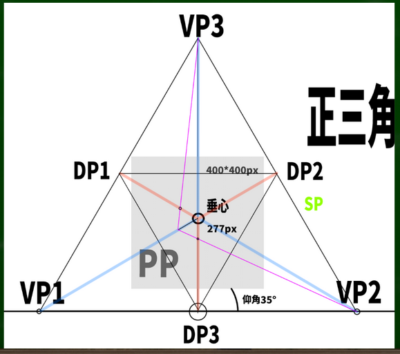
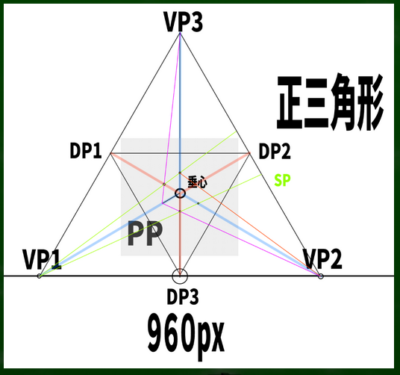
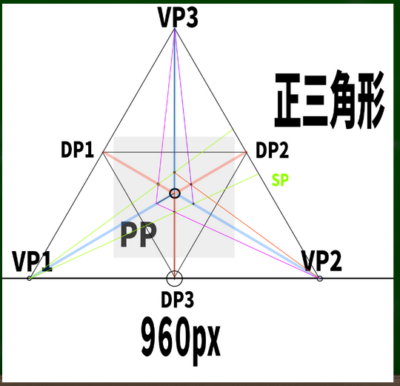
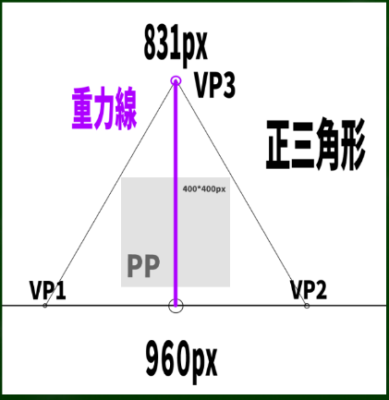
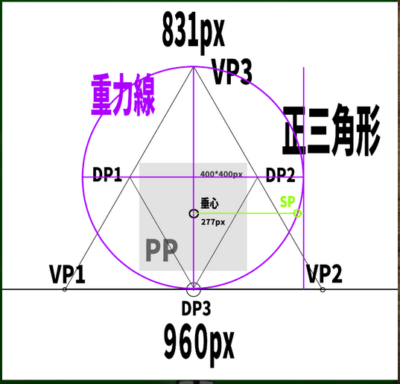
正三角形の高さの求め方は一辺をaとすると､(a×√3)/2である｡仮に２つの消失点の間の長さが960ピクセルだとすると､(960×√3)/2=831となる｡
この正三角形内に画面(PP)を設定すれば､最もベーシックで簡単な三点透視図法が完成する｡ためしに400*400pxの画面を構成してみた｡
正三角形の垂心の探し方
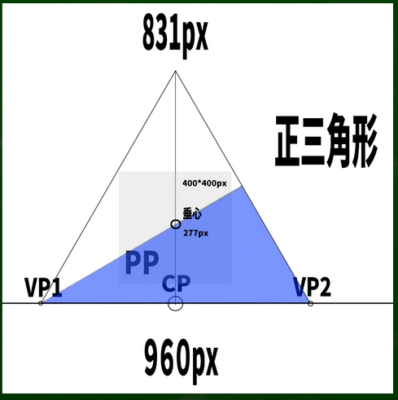
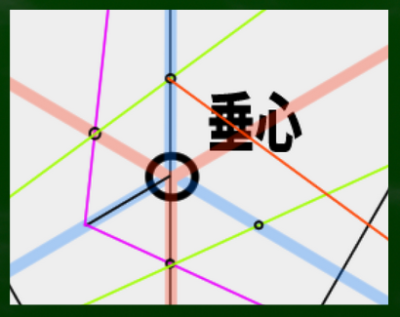
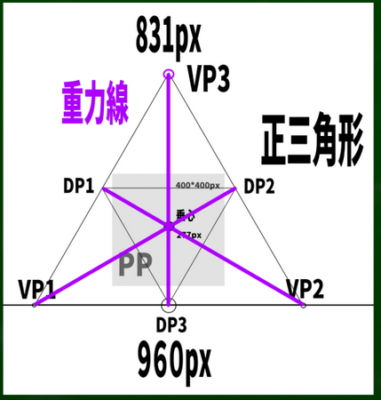
さて､この正三角形の垂心はどこにあるのか｡直角三角形を使って見つけてみると､ここにあることがわかった｡
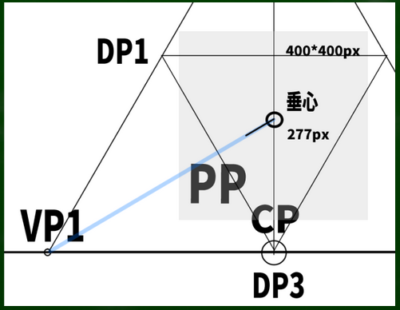
正三角形は便利な公式が使えるようだ｡正三角形の高さの1/3あたりの位置に交わる点がくる｡すなわち､831/3=277あたりの位置に垂心がくることになる｡
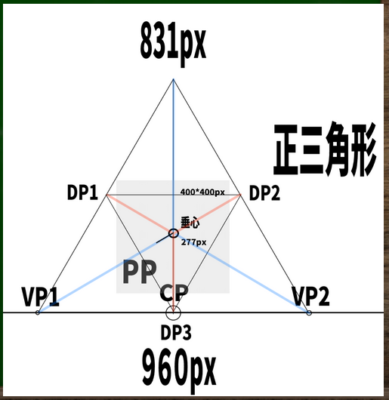
さらに逆三角形を内部に構成すると､対角線の消失点(DP)の位置が３つ判明する｡
正三角形の三点透視図法を用いて立方体を描く方法
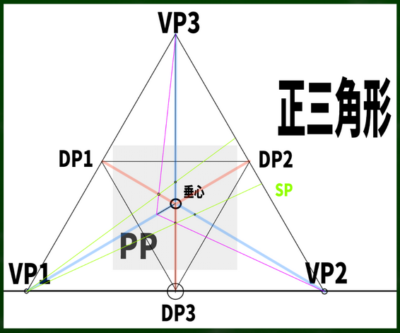
たとえば任意の点から適当な長さの斜線を垂心からVP(消失点)１へ伸ばしてみる｡
問題は､この斜線と実測で同じ幅の残りの斜線をどうやって引くかである｡
まずは各DPへと補助線を伸ばしていく｡
ここから適当に補助線へと線を伸ばしていくだけでもそれなりの立方体を構成することができるが､今回は少し丁寧に構成する｡ざっくりとした構成については最後のグリッド線の項目ですこしだけ扱う｡
次に､最初に引いた直線からVP３へ向かって線を伸ばしていき､VP３と補助線が交わる点の位置を見つける｡
アナログの場合はいちいち線を描かずに､紐やパース定規で線を伸ばしたりすることもある｡
VP２にも線を伸ばし､補助線と交わる点を見つける｡
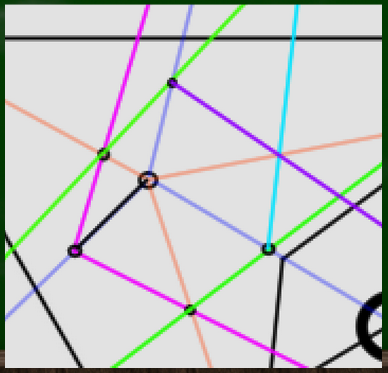
VP１から先ほど設定した２点へ線を伸ばしていく｡そうするとさらに補助線と２つ交わる点が見つかる｡
VP２からも同じように線を伸ばしていく｡
さらにVP３へむかって線を引けば､すべての辺の長さが確定する｡
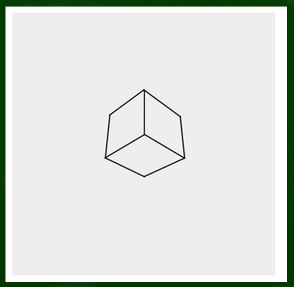
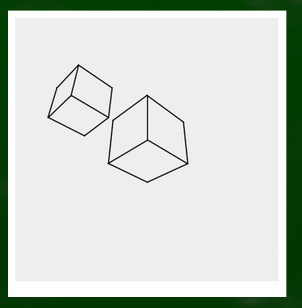
完成した立方体はこちら｡わりと綺麗な立方体ができたのではないだろうか｡
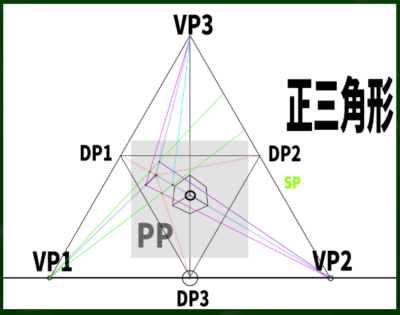
ためしに違う立方体も作ってみた｡
きれいにすると､このようになる｡
しかしまだまだ謎の部分が多い｡たとえば立点(SP)はどこにあるのか､視円錐はどこにあるのか､他の三角形だとどうなるのか､他の透視図法との関係はどうなるのか､疑問が山積している｡
【応用】三点透視図法における重力線と立点､仰角/俯角を見つける
重力線とはなにか､意味､定義､わかりやすく解説
先程の正三角形の三点透視図法をもとに､重力線をみつけていく｡
重力線：物体が重力によって垂直に立つ際に基準となる鉛直線であり､画面上の鉛直方向(上下方向)を示す線のこと｡
重力とは､簡単に言えば地球がものを下に引っぱる力のことである｡たとえば林檎を手から離すと､林檎は下に向かって落ちていく｡
宇宙ではこうした重力がないため､林檎は下に向かって落ちていかない(ほとんど感じられないほど重力が弱い)｡
三点透視図法における重力線の見つけ方
パースフリークスさんの説明をもとに検討していく｡
たとえば三点透視図法の場合､上下の消失点から垂直線を引くと､その線が重力線となる｡
まっすぐだけではなく､斜めの場合も重力線といえるらしい｡
たとえばこのような斜線も重力線となる｡
では､重力線がわかったところで､作図にどのように関わってくるのか｡
重力線を用いて立点を見つける方法
重力線は｢立点(SP)｣の位置を把握するさいに使うことができる(正確には､側面図における立点)｡
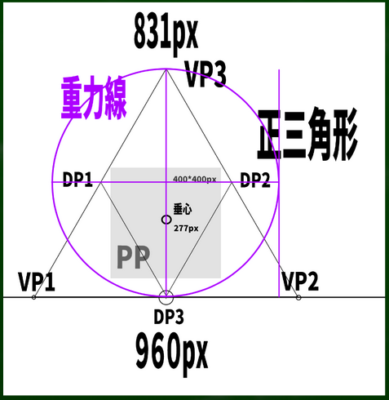
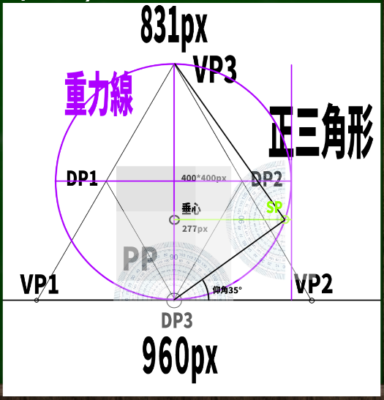
重力線の幅を直径として用いて､円を構成する｡コンパスを使うか､正方形を用いて円を構成する｡
こうしてできた円と､垂心から水平に伸ばした線が重なる位置が｢立点(SP)｣となるらしい｡頭の中ははてなマークだらけだが､とりあえず進めていく(側面図における立点という概念を理解する必要が出てくる)｡
立点と視円錐の関係なども謎のままである｡とりあえず､ここではSPの位置の求め方だけをおさえとくことにする｡
仰角､俯角とはなにか､意味､定義､わかりやすく解説
仰角(ぎょうかく)：説見上げる角度｡
俯角(ふかく)：見下ろす角度｡
三点透視図法における仰角や俯角の探し方を紹介する｡基本的に分度器が必要になる｡
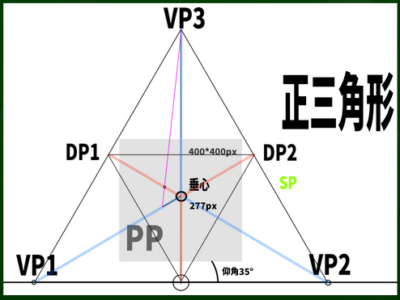
たとえばさきほどの正三角形の場合は煽りの図なので､仰角となり､図ってみると35°となっている｡
仰角がわかったところでどうなるのか､という問題は後回しにする｡また､なぜDP３とSPとを結んだ角度が仰角になるのかという点も後回しにする｡
【応用】三点透視図法における３つ目の消失点の探し方
観察者は目の前の風景をどのように見ているのか
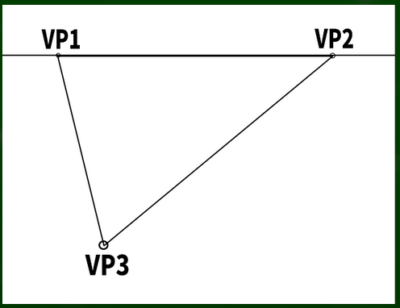
まず､二点の消失点を端に設定する｡つまり､これがVP１､VP２になる｡問題は上下のVP３がどこにあるかという点である｡これは正解･不正解というより､どう設定するかの問題になる｡
まず､観察者が目の前の風景をどのように見ているのかという点がポイントになる｡
- 見上げているのか､見下ろしているのか
- それらの仰角や俯角は何度か
このあたりはまだ理解できる｡
次に､自分の上か下に立方体があるとして､それは何度に傾いて見えるのか｡
ここが難しい｡そもそもなぜそれを知る必要があるのか､いまいち理解しにくい｡
三点透視図法における角度を理解する思考実験
たとえばこの立方体と観察者を真上から見た場合､立方体は何度に傾いているように見えるのかという思考実験を行ってみる｡
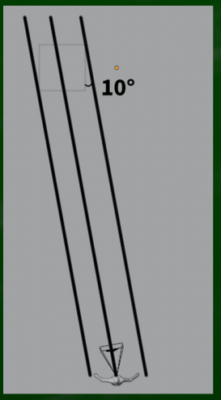
観察者からまっすぐ線を伸ばし､角度を測ると､およそ１０度くらいだった｡
blenderでいえば､Z軸に１０度カメラが左に傾いていることになる｡
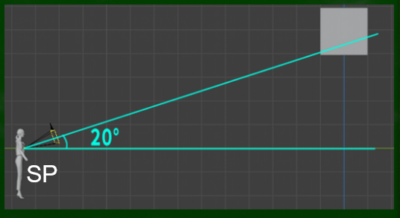
では仰角は何度なのか｡横から見た角度を測れば､何度かわかる｡blenderで言えば(90度から)20度縦にカメラが傾いていることになる(ピッチが回転している)｡これが側面図における立点という意味合いなのだろう｡
仰角２０度､横の傾きが１０度の場合の画面のケースがこちら｡
下は仰角０度(90度)､横の傾き０度のケースである｡先ほど見えていた立方体は見上げなければ画面に入ってこないということがわかる｡
三点透視図法における３つ目の消失点を探す方法
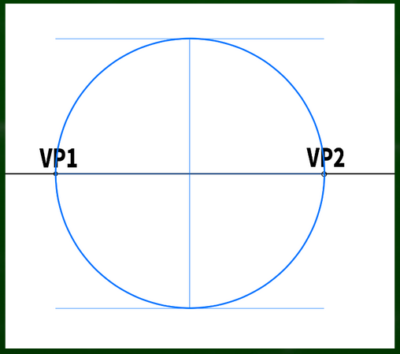
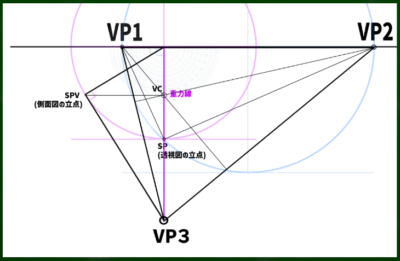
VP３の位置を探していこう｡まずはVP１からVP２の長さを直径とする円を構成する｡半円でもいい｡
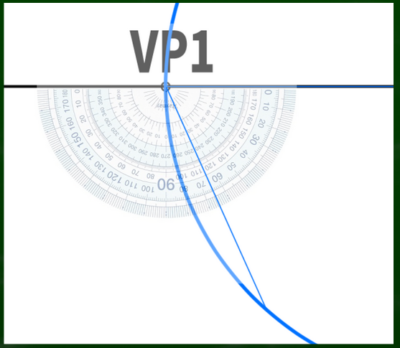
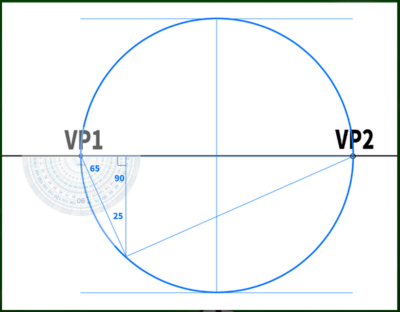
たとえば２５度の回転(ヨー)をつけるためには､VP１から６５度の方向に向かって半円と接するまで線を引けばいい(90-25=65)｡
このように三角形を構成すると､ちょうど２５度になる(三角形の内角の和は１８０度)｡
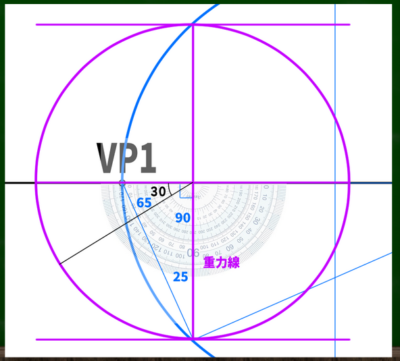
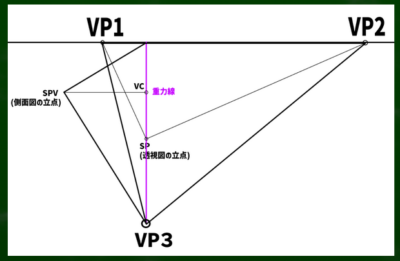
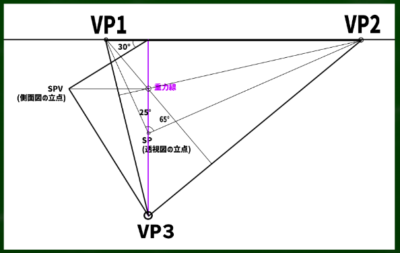
重力線を利用して､今回は３０度の俯角を作っていく｡重力線と同じ長さの線を３０度の方向に引いていく｡
引いた先が側面図の立点となる｡ちょうど先程blenderの画面で見たような側面図をイメージするとわかりやすい｡
SPVから垂直に線を伸ばしていき､重力線と交わる点がVP３となるようだ｡
三点透視図法の三角形を構成すると､このようになる｡適当に鋭角三角形を構成することもできるが､自分がどのような角度で対象を見たいかを考慮しながら透視図法を構成するスキルが必要になる｡つまり､正解不正解の領域ではなく､センス･美的間隔の領域となる｡
【応用】三点透視図法における視円錐の探し方
三点透視図法における視円錐の構成方法
三つの消失点がわかっただけでは絵を描くことはできない｡画面(PP､キャンバス)を構成しないといけない｡
画面を構成するためには､歪まない範囲を知る必要がある｡すなわち､人間にとって自然な視円錐を知る必要がある｡
円錐(Cone of Vision､COV)：透視図法において、観察者が自然に見ることができる視界の範囲を示す概念のこと｡
まずは先程のSPVからまっすぐ水平線を伸ばし､重力線と交わる点を見つける｡この点が視心(VC)となる｡
ちなみにこのVCは､VP１､VP２､VP３からなる三角形の垂心となる｡
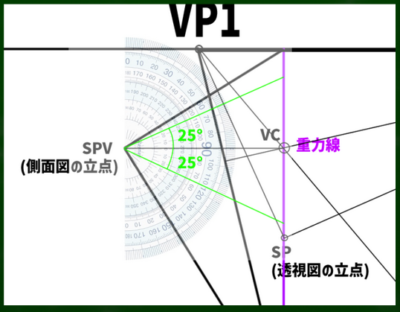
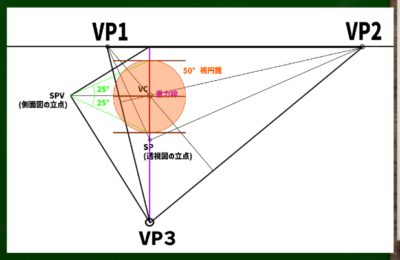
三点透視図法の場合､視円錐は６０度以内に保つことを以前の動画で学んだ｡今回は５０度で構成してみる｡
SPV(側面図の立点)から左右に２５度ずつ線を伸ばせば､合計５０度の視円錐を構成することができる｡
あとはこの直径をもとに､視円錐を構成していく｡
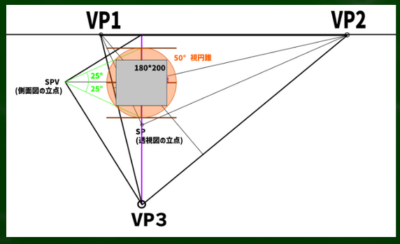
最後に､この視円錐内に画面を構成すれば完了となる｡
たとえばこのように画面を構成してみた(180*200px)｡もっと画面を大きくしたい場合は､VP１とVP２の距離をもっと離せば可能になるのだろう(今回は960px)｡
なにをやっているかよく理解できない上に､しかも毎回こんな煩雑な作業をするのかと感じている人がいるかもしれない｡同感である｡
しかし一通りやってみることがまず重要である｡汎用性の高いキャンパスを一度構成すれば､使い回すことも可能になってくる｡
もう少し大きな視円錐を構成してみる
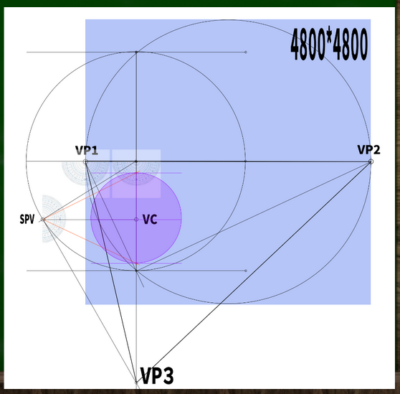
たとえば汎用性が高い､A4サイズの595*842をPPにしたい場合､いったいどのように消失点を設定すればいいのだろうか｡
正確な計算は正直まだわからない｡しかし単純に､ここ(960px)からおよそ５倍すればいいのではないだろうか｡つまり､VP１からVP２の距離を4800pxとすればいいと仮定してみる｡これがアナログなら､センチで考えるといいのかもしれない(もちろん､センチならもうすこし数が小さくなるだろう)｡
さて､ここからは以前の手順のとおりなので省略する｡テストなのでかなり角度はざっくりと作成した｡
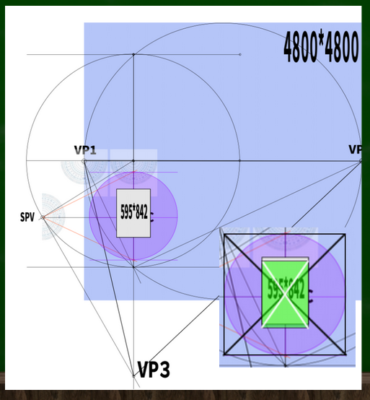
この視円錐(50度)を元にA４サイズのPPを構成してみる｡余裕で入ったので､もうすこし小さなサイズでもよかったのかもしれない｡
また､PPの中心ができるだけ視心と重なるようにPPを設置したほうが､よりバランスをとることができる(図では中心にきてはいないが)｡
【応用】三点透視図法における測点と対角線の消失点の探し方
三点透視図法における測点を探す方法
正三角形の三点透視図法での立方体の作成方法は学んだが､他の三角形の作成方法は学んでいない｡また､どんな三角形でもいいというわけではなく､鋭角三角形(3つの内角すべてが90°未満の三角形)である必要がある(直角三角形もだめらしいが､このあたりに今回は触れない)｡
立方体を構成するためには測点(MP)や対角線の消失点(DP)を把握する必要がある｡これがややこしい｡今までで一番理解しにくい｡
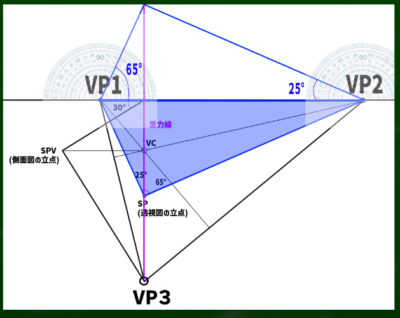
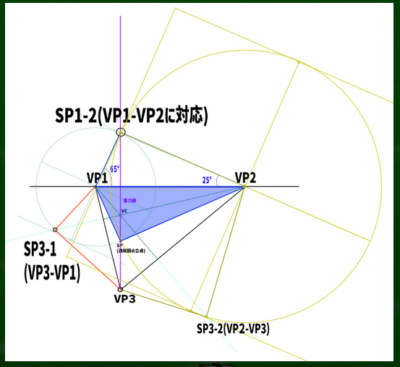
図は先程扱ったものを使用する｡仰角は３０度､角度は左に２５度､右に６５度である｡
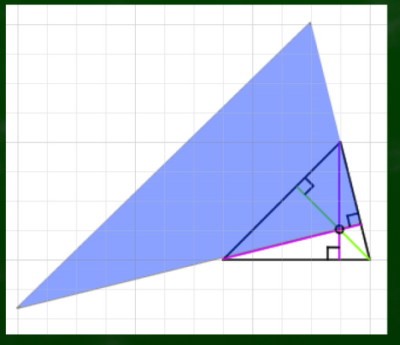
まずはこの青い範囲の三角形を､上にも上下反転させてつくる｡どうやってか｡
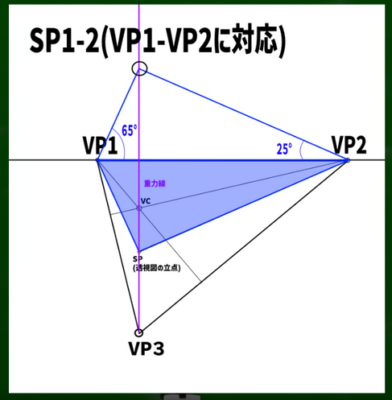
まず重力線を上へ延長する｡そこから､左は６５度の角度で､右は２５度の角度で重力線へと伸ばしていく｡そうするとそれぞれの線が交わり､反転した三角形ができる｡
新しくできた点をSP1-2とする｡なぜここが立点(SP)なのかというはてなマークは置き去りにして進めていく｡
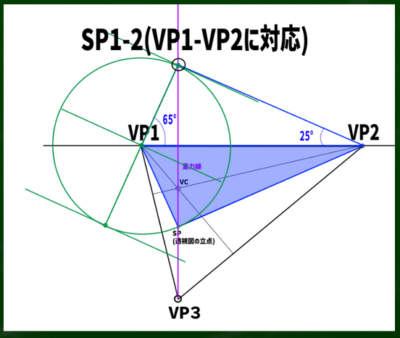
次に､VP１からSP１-２までの長さを利用して､正円を構成する｡
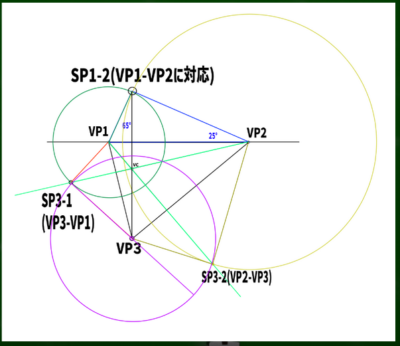
VCから線を延長して伸ばしていき､円と交わる点をみつける｡この点がSP3-1(VP3-VP1に対応)となる｡
同じようにしてSP3-2も見つけていく｡
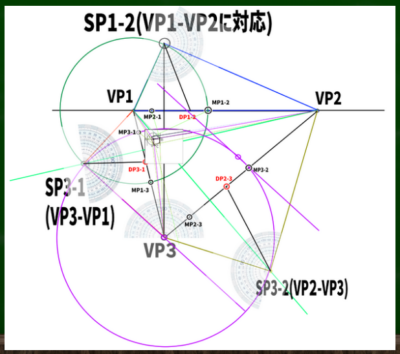
図をスッキリさせるとこのようになる｡
ここから測点を探していく｡
測点(Measuring Point,MP)：追加の便宜的な消失点のような役割をする点｡特定の消失線上(主に水平線上)に位置し､透視図において物体の寸法を正確に測定するために用いられる便宜的な点のこと｡
要するに､立方体を描くために必要な点というわけだ｡
測点を探すために､最後にもうひとつ円を構成していく必要があるらしい｡面倒だが､難解な数学のように理解できない作業ではないのでその分､気が楽だ｡
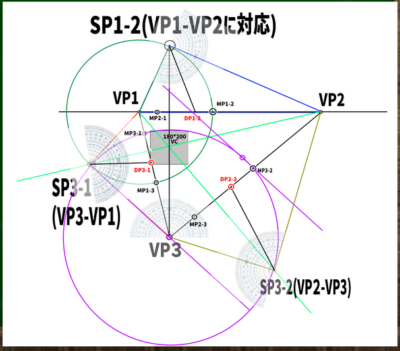
SP3-1からVP３の長さを直径とした円を構成する｡
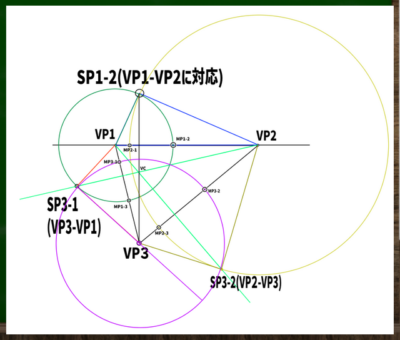ここから､円と接する線を合計で６つ探していく｡なぜそこがMPになるのかの原理はいまいち理解していないが､まずは慣れていくことにする｡
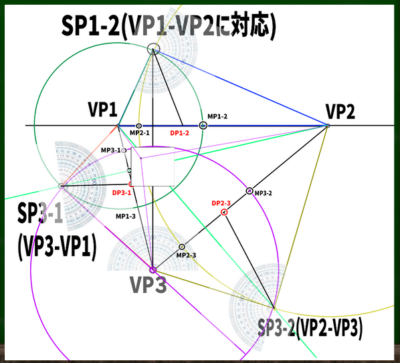
次に､対角線の消失点(DP)を探していく｡各SPから､ちょうど半分の角度になるような方向に線を伸ばした位置がDPになるようだ｡つまり､４５度の位置ということになる｡これでDP１-２､DP２-３､DP３-１の位置がわかる｡
【応用】他の三角形の三点透視図法で立方体をつくる
測点を用いて三点透視図法で立方体を作る方法
前回の項目で､三点透視図法の測点と対角線の消失点を把握する方法を見てきた｡このMPとDPを使って立方体を構成していこうと思う｡
さきほど構成した図がこちらである｡ここに､適切な画面を構成する｡これも前の項目で構成した画面をそのまま利用する｡
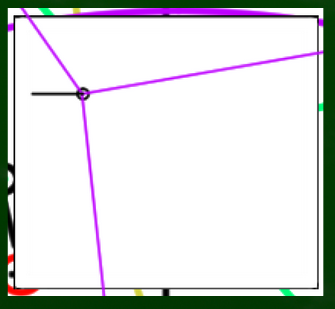
まずはPP内に描きたい立方体の中心点を任意に設置する｡たとえばここにしてみる｡
中心点から､各消失点へ線を伸ばしていく｡
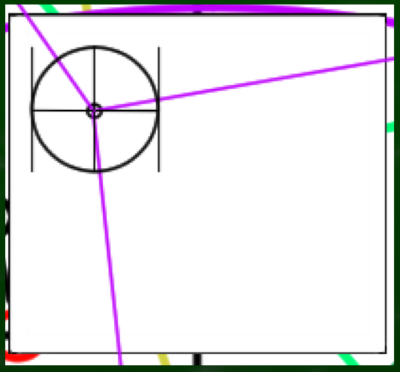
次に､任意の直線を水平または垂直に構成する｡たとえばこれくらいの長さの辺の立方体を構成したいとする｡
引いた長さを半径とした正円を構成する｡
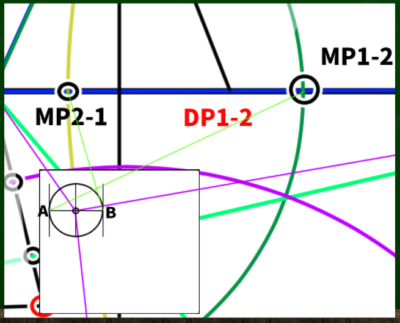
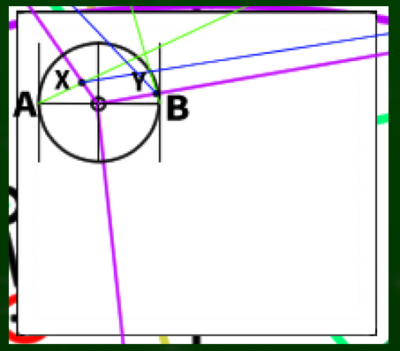
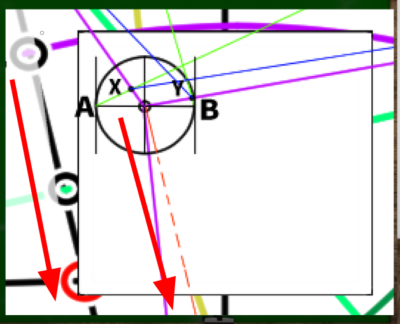
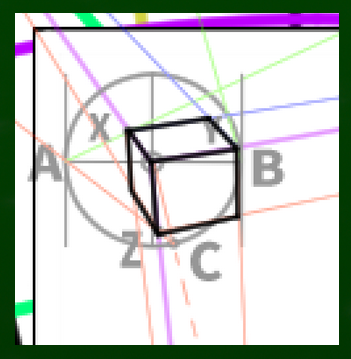
AからMP1-2へ､BからMP2-1へと線を伸ばす｡
線を伸ばしてできた新たな交点をX､Yとする｡そこからさらにVP１､VP２へと線を伸ばしていく(XをVP2へ､YをVP1へクロスさせるように伸ばす)｡
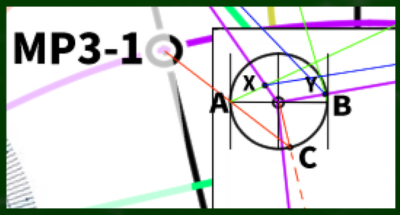
次に､円の中心から線を円の端まで伸ばしていく｡このときの角度は､VP１とVP３を結ぶ線と並行になるようにする｡角度は分度器などで測るとより正確に描くことができる｡
円と接した交点をCとする｡このCからさらにMP3-1へと線を伸ばしていく｡
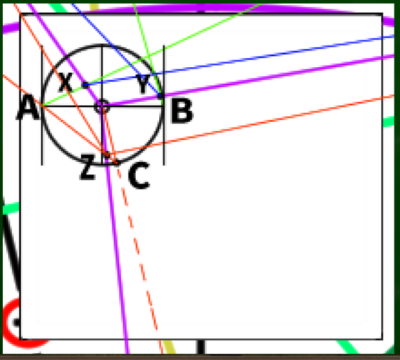
新しくできた交点をZとする｡このZからさらにVP1､VP２へと線を伸ばしていく｡
さらにXとYから､VP３へと線を伸ばしていく｡
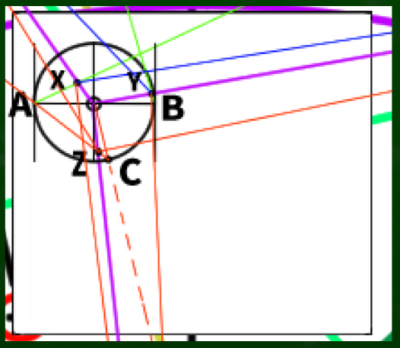
あとはそれぞれの交点を結ぶだけで立方体が完成する｡
できあがった立方体だけをきれいに表示すると､このようになる｡ざっくりと透視図をつくったわりにはキレイな立方体ができた｡
立方体をつくるために､何倍もの面積と手間がかかるのは大変かもしれない｡しかしアナログの手法も覚えておいて損はないだろう｡また､この透視図法は一度作れば使い回しが可能である｡
(2-9)【応用】三点透視図法グリッドを作成する
三点透視図法をグリッドを使ってざっくりと利用する方法
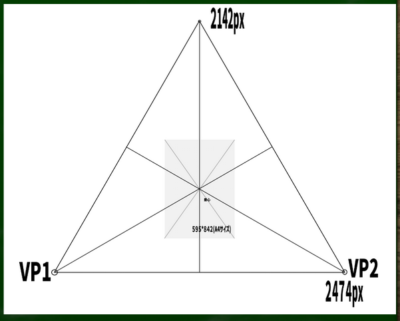
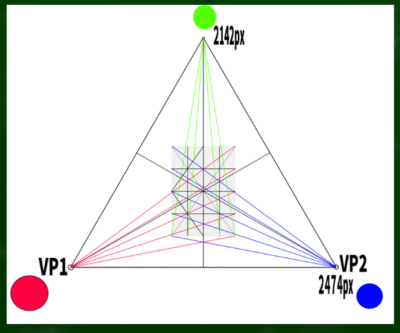
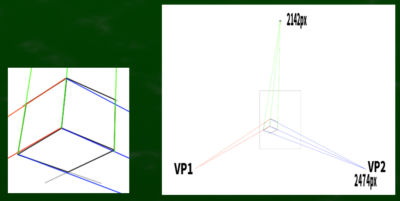
今回はA４サイズが画面に来るように正三角形を作ってみた｡
仮に一辺が2474pxだとすると､高さは√3/2×2474≒2142となる｡もっと小さい正三角形でもおそらく可能かもしれないが､とりあえず二点透視図法で使用した数字を今回は使用してみた｡
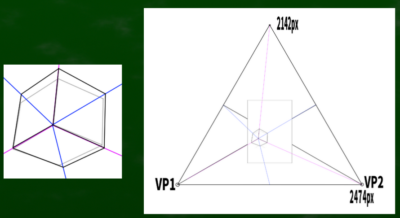
視円錐などは特に考えず､三角形に余裕をもって収まれば歪みは少ないと仮定する｡ただし､PPの中央にはできるだけ垂心がくるように考慮する｡ちなみに(正三角形の場合)垂心はおよそ高さの1/3あたりにくる(2142*1/3=714)｡
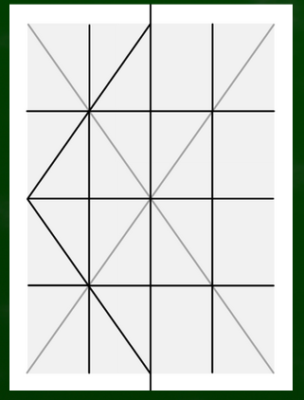
次に､A４サイズに適当にグリッドを作成する｡今回は4×4のマスをつくる｡ざっくりでもOK｡長方形をクロスさせればその中心が1/2の高さとなることを利用する｡もちろん定規を使ってもいい｡
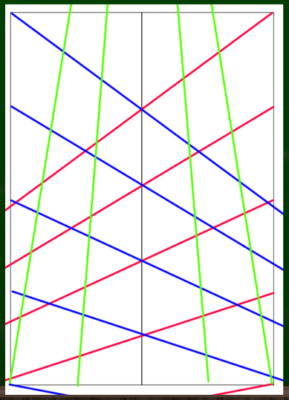
最後に､それぞれのグリッドに向かって各消失点から線を伸ばしていく｡
画面をスッキリさせるとこのようになる｡
このグリッド線そのものを使うというより､グリッド線の角度を参考にするイメージになる｡
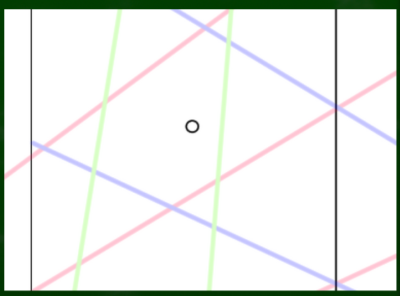
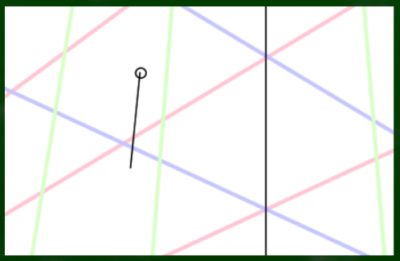
たとえばこのあたりに立方体を描きたいとする｡そこに丸をつける｡
そこから適当に下に線を引く｡下への線は緑のグリッド線(VP3線)を参考にして､ざっくりとおろす｡近くの緑の線と似た感じ､平行気味になるようなイメージがポイント｡
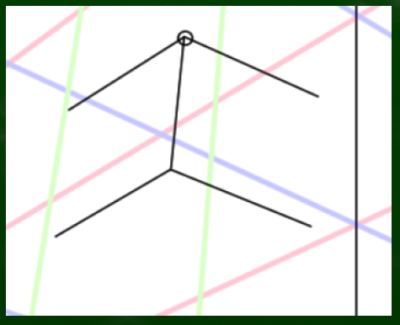
左右に､同じようにグリッドを参考にしながら線を引いていく｡今回は立方体を描くわけではないので､長さは任意でOK｡
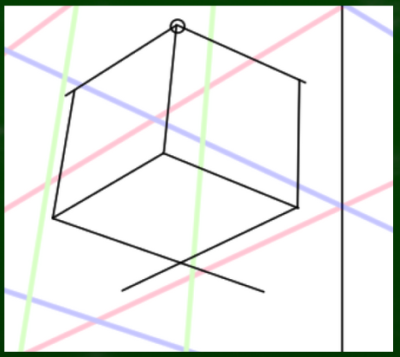
あとは適当につなげていくだけで､それっぽい三点透視図法の立方体を構成することができる｡
もっとグリッド線を引けば､さらに正確な近似が可能になる｡たとえば16マスよりも32マスのほうがより正確な遠近感を表現できるといえる｡
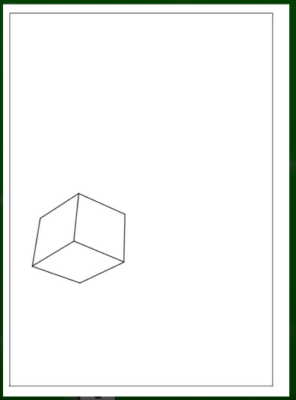
きれいにしたものがこちら｡
ざっくりとビルを描きたいときやアタリをとりたいときは便利かもしれない｡
ちなみにもっと正確に描けばこのようになるが､そこまで違いはない｡
きちんと立方体を構成するとこのようになる｡
参考文献
初心者でもわかりやすい本
ロビー・リー「超入門 マンガと図解でわかる! パース教室」
・パース全般の基礎において一冊目にこれを手に取るのに適している｡ ・私は「パース！マンガでわかる遠近法」よりも平易に､かつ丁寧に説明されていると感じた｡それゆえに､初心者は特に一冊目にこの本をおすすめする｡
デヴィッド・チェルシー「パース！マンガでわかる遠近法
・イラストが多く､わかりやすい｡パースの基礎用語の説明もされていて､かつ平易にパースの使い方が説明されている良本｡ただし､建築パースに特化しているわけではなく､「イラストレーション(漫画)」に特化している点を注意する必要がある｡ ・パース全般の基礎を学ぶという目的において一冊目にこれを手に取るのに適している｡
上級者向け
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
絵を描く､特に線画に特化した本｡小難しいが広く､深く説明されている良本｡
山城義彦「現代パースの基本と実際」
・パースの歴史や細かい用語が説明されていて便利｡ただしメインはイラストレーションではなく「建築パース」に特化している点を注意する必要がある｡ ・かなり小難しく説明されている(建築パースゆえにそうならざるをえないのだろう)｡例えるなら文系が理系の数学を見たときのあの感覚に近い｡建築家ならば通らなければならない道ではある｡ただし､この本はだいぶ古く､現代ではコンピューターグラフィックスをもっと多用して楽をするのだと感じた｡ただし､楽をするにもその原理を知っておいて損はない｡
その他
参考サイト:パースフリークス(URL)
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
・全般的な絵の知識が語られている本であり､パースに割かれる箇所は少ない｡ただし､それなりにそれぞれ濃く説明されている本である｡ ・パースを学ぼうとしてとる本ではないが､絵の描き方を学ぼうとする場合は選択肢に入ってくる｡ただし高いのが難点｡
コメント