目次
はじめに
動画での説明
・この記事の「概要・要約」はyoutubeの動画の冒頭にありますのでぜひ参照してください。
よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m
三点透視図法とはなにか、意味、定義、わかりやすく解説
三点透視図法:左右二つと、上下どちらか一つの消失点を使う線遠近法のこと。
見上げているときか見下ろしているときや対象と肩とが斜めになっている場合などに使われる。
定義だけを見てもさっぱりわからない。三点透視図法がパースで一番難しいと言われることが多い(特に作成方法において)。
・今回は三点透視図法の具体的な作成方法、種類(構成する三角形の角度など)には触れない。次回、(おそらく扱える方法や種類はごく一部になるだろうが)扱う予定である。
・今回の主要課題は「他の透視図法との違いを知ること」、「メリットとデメリットを知ること」の2つである。
画面の中心にある立方体は何面見えているか
一点透視図法の場合の面
以前も扱った内容なので、今回は少しだけ違う角度から考えてみる。たとえば画面がこのような場合、一点透視図法であることを学んだ。なぜなら、視心(画面の中心)の立方体が1面しか見えていないからである。
このカメラを上下左右、どこに動かしたとしても一点透視図法であることに変わりはない。
言い方を変えれば、撮影者の肩は真っ直ぐであり、斜めを向いていない(目玉、視線を動かさずに、真っ直ぐ向けている)。たとえば先ほどの画面からすこし右にカメラを動かしたとしても、一点透視図法にかわりはない。
立方体の面が2つになってしまったから二点透視図法なのではないかと思う人もいるかもしれない。
 しかしカメラそのものが(ズームなどではなく)物理的に動くということは、視心も動くということになる。カメラの視心の位置に立方体を設置すれば、見える面が1つだけの画面を構成できる。
しかしカメラそのものが(ズームなどではなく)物理的に動くということは、視心も動くということになる。カメラの視心の位置に立方体を設置すれば、見える面が1つだけの画面を構成できる。
つまり、カメラを上下左右に水平もしくは垂直に移動させようと、透視図法の種類が変わるわけではないということである。
重要なのは「カメラの角度(目玉の角度)」であり、視心の立方体と平行であるかどうかである。カメラを傾けることと、移動させることのニュアンスの違いが重要になる。
二点透視図法の場合の面
すこしカメラを左右に傾け、その視心に立方体を構成してみた。視心には2面見えるようになり、二点透視図法であることがわかる。
この傾け(回転)の種類については後でピッチ、ロール、ヨーの三軸ごとに説明する。
ここで重要なのは、肩が対象と平行になっていないという点である。立方体側からすれば、肩は斜めになっている。肩側からすれば、立方体は斜めになっている。
左右にカメラを傾けたから、その分斜めになるのである。
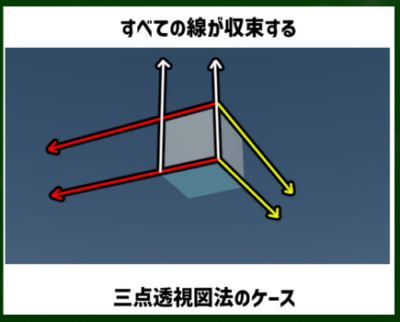
三点透視図法の場合の面
察しの良い方はわかったかもしれないが、三点透視図法では「上下にカメラを傾ける」ということになる。また、視心に見える面の数も3つだろうと推測できる。
上にカメラを傾けたら煽り(あおり)、下にカメラを傾けたら俯瞰(ふかん)と呼ばれる。
さきほどの二点透視図法の画面を、カメラを上に傾けてみる。また、その視心に立方体が来るように移動させる。
そうすると、今回のケースではたしかに三面見える。
頭の位置を上下すること、頭を傾けること、目玉を傾けることの違い
それぞれのケースの比較
「頭(体)は回転して、目玉が回転しないケース」と「頭(体)は回転しないが、目玉が回転するケース」を正確には区別する必要がある。
体が回転すれば実質的にカメラも少し上下する。ただし、体の回転で下がった視高を補うような台座を設置すれば、実質的に同じような景色を構成することはできる。
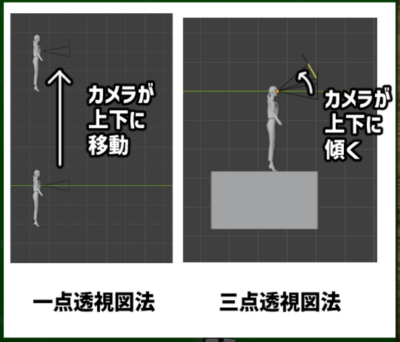
図にするとこのようなイメージになる。
これはカメラが上下に移動する場合と、上下に傾く場合の違いの図である。
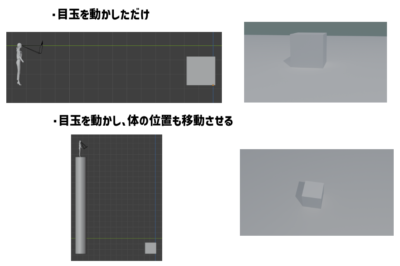
目玉を動かした程度では、わかりやすい煽りや俯瞰の構図は得られにくい
実際には目玉を動かす程度では煽りや俯瞰がよくわかりにくく、体の位置の上下の変化を必要とするだろう。
ビルの屋上に行って見下ろすのと、地上から自分の身長の高さから見下ろすのとはかなり違う。
(頭ではなく)目の角度を変えたら目の高さは変化するのか?
- Q1「(頭ではなく)目の角度を変えたら目の高さは変化するのか」
- A1「しない。ただし、目ではなく頭の角度を変えた場合は、微量に変化する。体全体の角度を変えた場合は、場合によって大きく変化することがある」
- Q2「目の高さ、視点の位置は変化していないが、視線の方向は変化している。つまり、目玉が上下に回転しているだけであり、目玉そのものは移動していない。」
- A2「目の高さ、視点の位置は変化していないが、視線の方向は変化している。つまり、目玉が上下に回転しているだけであり、目玉そのものは移動していない。」
- Q3「なるほど、視点の位置が同じだということが目の高さが変わっていないという説明だということは理解した。しかし、実際に画面内の地平線の位置が変化していることはどのように説明するのか」
- A3「地平線が見かけ上、上下に動いているだけであり、実際の地平線は動いていない。視覚的な効果にすぎない。視点の高さが変わっていなくても、カメラの角度を変えることで見える範囲が変化し、地平線の位置が変わったように感じるだけ」
- Q4「・・・?」
地平線について理解する
まずは「地平線(水平線)」という概念について理解し直していこう。
地平線(HL,水平線):見ている人の目の高さを示す、仮想の水平な線。見ている人の目と同じ高さにあるものは、この線と必ず重なる。
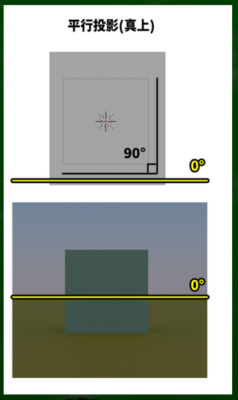
地平線をわかりやすいように設定してみた(画面は一点透視図法)。一般的には地面と空の境界の線である。海と空の境界の線でもいい。
この地平線(水平線)の角度は一般に0°(真横の線)となる。もちろん、地球は球体なので宇宙から見れば直線ではなく曲線なのだが、局所的に見れば直線に見えるだけということには注意する必要がある。
地平線は一般に、目の高さと一致すると言われている。さて、ここで重要なのは「(頭の角度ではなく)目の角度を変えたら目の高さは変化するのか」という問いである。
答えは、変化しない(と考える)ということになる。あくまでも身長が高くなったり、高所に移動することで目の高さは変わると考えていく。
カメラを上下に移動させた場合の平行線
たとえばカメラを上下に移動させると、水平線の位置は変わらず画面の中心に来る。
左右にカメラの角度を動かした場合の平行線
二点透視図法の場合は左右に首を傾ける。そのため、一点透視図法と画面の地平線の高さは共有され、(見かけ上も)同じであるといえる。
例えば左に首を傾けても地平線の位置は変わらない。
上下にカメラの角度を動かした場合の平行線
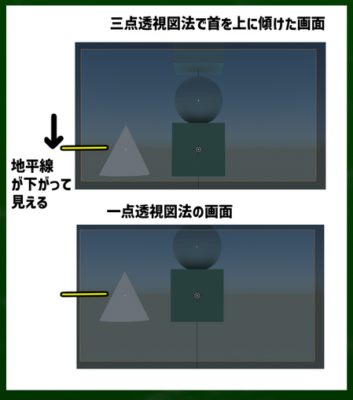
三点透視図法の場合は上下に首を傾ける。
すると、地平線の位置が一点や二点透視図法と変わったように見える。
三点透視図法ではなぜ水平線が変化するのか
「視覚的な感覚としては、目線を上や下に動かすことで地平線が上下に動いたように感じる」というニュアンスがいまいち理解しにくい。
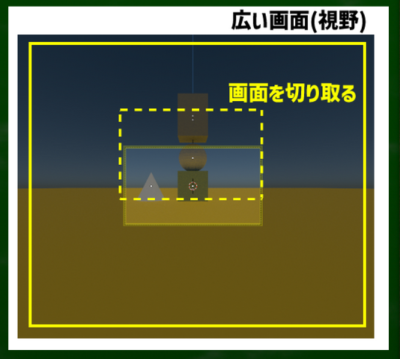
もし人間がとんでもなく視野が広い生き物だとする。「もし一点透視図法で上下の視野が見えていたら、このように見えていた」という画面を切り取ったようなイメージを考えてみる。
たとえば通常、一点透視図法で自然に見える画面の範囲はこのくらいしかないとする。
しかし、とんでもなく広い視野の持ち主なら、このように画面が見えている可能性がある。また、そこから任意の画面を切り取れば、このように地平線が下がって見えるような画面を構成することができる。
つまり、見かけ上、地平線を上下させることができる。
もちろん、これは自然な範囲の画面内で切り取ることでも、見かけ上、地平線を下げることは可能である。一点透視図法で地平線が上下にある場合は、切り取っているケースがほとんどである。
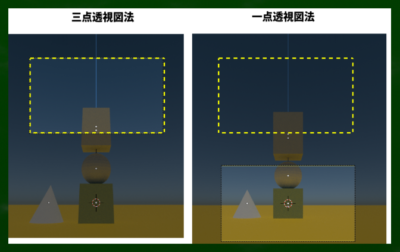
また、このようにして画面を切り取ったとしても、三点透視図法と同じような画面にはならないという問題がある。
- 目玉を上下に傾けた場合、一点透視図法と三点透視図法の地平線の位置は同じである。
- 目玉を上下に傾けた場合、一点透視図法よりも消失点が増えることにより、収束する線も増え、異なる画面が構成されるようになる。
- 三点透視図法の本質は地平線の高さの違いではなく、収束のあり方である。
煽り、俯瞰とはなにか
三点透視図法における煽りとはなにか、意味、定義、わかりやすく解説
煽り(仰角視点,あおり):物体を下から見上げる視点のこと。
・視点が物体よりも低く、上に向かって見ることで、物体が大きく、威圧的に見える効果を生む。
・視線が下から上へ向かうため、収束点が上側に位置する。
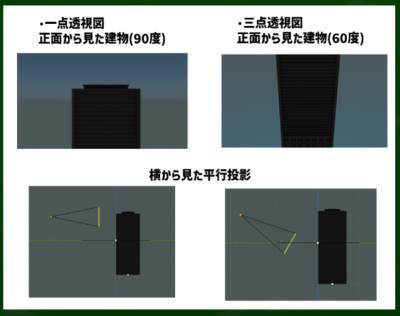
たとえばカメラの角度(目玉)を90度(まっすぐ)から120度(上)に上げれば、煽りの画面が構成される。
三点透視図法における俯瞰とはなにか、意味、定義、わかりやすく解説
俯瞰(俯角視点,ふかん):物体を上から見下ろす視点。視線が上から下に向かう。
・ 物体が小さく、圧倒的に、支配的に、遠く感じられることが多い。
・視線が上から下へ向かうため、収束点が下側に位置する。
たとえばカメラの角度(目玉)を90度(まっすぐ)から60度(下)に下げれば、俯瞰の画面が構成される。
ピッチ、ロール、ヨー
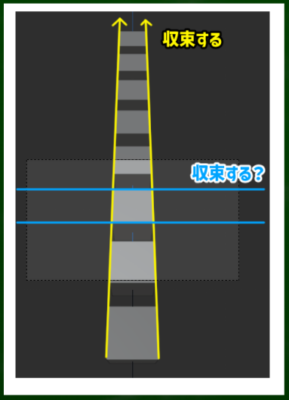
見かけ上、二点にしか収束しない三点透視図法がある?
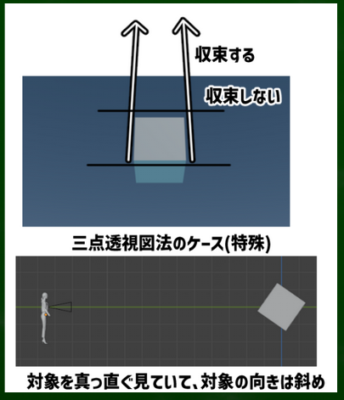
例えばこの画面ではたしかに上へと収束していくが、左右には平行で収束しないように見える。三点透視図法であるのにもかかわらず、収束する消失点が見かけ上、上下と奥にしか収束していない。つまり、見かけ上、二点透視図法と等価になっている。
フローチャート:「箱が斜めに置かれているか水平に置かれているか」、「箱の向きは見ている人に対して真っ直ぐか、斜めに置かれているか」
たとえばロビー・リーの本では「箱が斜めに置かれているか水平に置かれているか」という問いと「箱の向きは見ている人に対して真っ直ぐか、斜めに置かれているか」という問いが設定されている。
大前提:箱を見上げているか、見下ろしているという状況
問い1:「箱が斜めに置かれているか水平に置かれているか」
- もし斜めに箱が置かれていれば、三点透視図法を使う必要がある
- もし水平に置かれていれば、次の問いへ移行する。
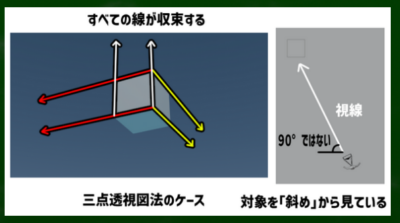
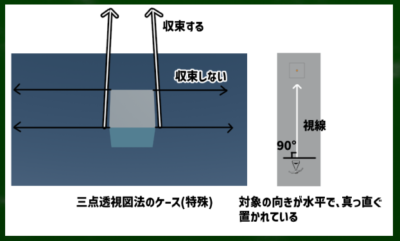
問い2:「箱の向きは見ている人に対して真っ直ぐか、斜めに置かれているか」
- 箱の向きに対して真っ直ぐ置かれていれば、「三点透視図法」を使う必要がある。「縦の二点透視図法」が使えるという点がポイントになる。
- 箱の向きに対して斜めに置かれていれば、「三点透視図法」を使う必要がある
さきほど収束しないように見えた図は、問い2の(1)のケースになる。
二点透視図法で縦の線が収束しないケース=三点透視図法で横の線が収束しないケース?
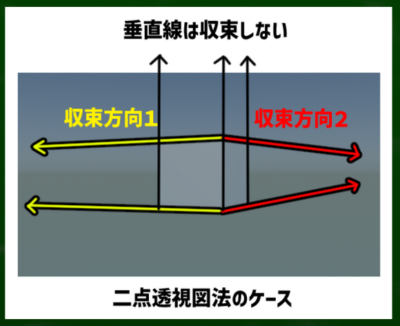
二点透視図法では横の線と奥行きの線が収束し、縦の線が収束しないことを特徴とすることを第5回の動画で学んだ。
二点透視図法の場合を図にするとこのようになる。
この二点透視図法をぐるっと回転させれば、さきほどの三点透視図法と似たような画面構成になるというわけである。
三点透視図法における斜めと水平
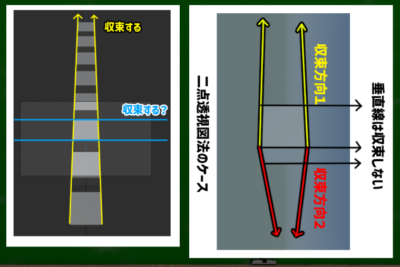
三点透視図法の場合は、垂直線も収束するという点がポイントであった。
上の画像の場合は対象が観察者に対して「斜め」に置かれている場合、下の画像は対象が観察者に対して「水平」に置かれている場合である。
水平の場合はなぜか、横の線が収束しないように見える。
つまり、視心の対象が水平に置かれているケースは、三点透視図法の特殊ケースだといえる。
ぴったり90度のケースでは垂直(上下)には収束するが、水平(左右)には収束しないように見えるケースだというわけである。他の角度、たとえば89度でも91度でも、すこしでも斜めになれば水平の線も収束し、三つの消失点へ収束するような画面になる(視認できるかどうかは別として)。
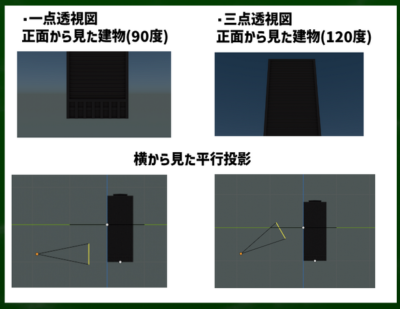
対象を正面から見たケースで三点透視図法の場合
他にも特殊ケースはありうる。三点透視図法では煽りか俯瞰だけだと私は思い込んでいたが、対象を正面から見たケースでも三点透視図法はありうる。
対象を正面から見ている絵であり、かつ、斜めに置かれているケースでは三点透視図法になる。これも特殊ケースであると言える。三点透視かどうかをチェックする方法は立方体に限っては簡単であり、単に垂直線が収束しているかどうかで判断できる。一点や二点透視図法では基本的に縦の線は収束せず、90°に伸びていてお互いに交わらない。
たとえばこの画面は対象を煽りや俯瞰ではなく、正面から見ていて、かつ対象が水平ではなく斜めになっているケースである。
このような特殊なケースでは三点透視図法でも横の線は収束しないように見える。
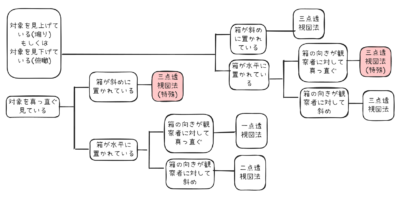
整理した図
整理するとこのような図にまとめることができる。
ピッチ、ロール、ヨーとはなにか、意味、定義、わかりやすく解説
ややこしいのは「箱が置かれている状況」である。ひとつひとつ整理していく。今回はピッチ、ロール、ヨーに区別して整理していく。
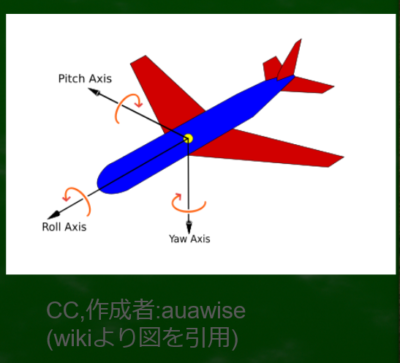
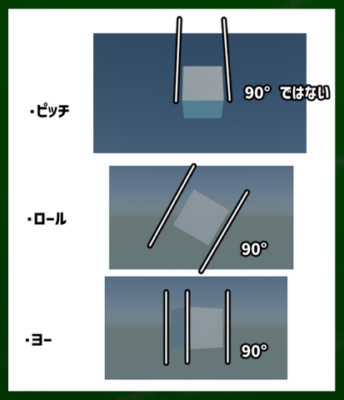
ピッチ:上下方向の回転(x軸)のこと
ロール:前後方向の回転(y軸)のこと
ヨー:左右方向の回転(z軸)
名称は媒体によって違うかもしれない。右の図を参考に感覚的に覚えたほうが早い。ピッチは前後に首が動き、ロールは首が傾き、ヨーは左右に首を動かすというイメージである。
Q箱が水平や斜めに置かれているとはいったいどのような状態なのか
(1)水平に置かれているケース
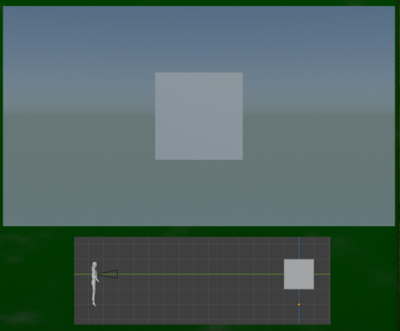 回転の度数でいえば、X、Y、Zの全ての角度が0°のケースが水平に置かれているケースである。
回転の度数でいえば、X、Y、Zの全ての角度が0°のケースが水平に置かれているケースである。
(2) 前後方向の回転(ピッチ / Pitch)
たとえば(1)をX軸に30°回転するとこのようになる(他の軸は0°に制御)。
このケースでは垂直線は収束しているが、横の線は収束していないように見える。このケースは三点透視図法の特殊ケースであった。このケースでは二点透視図法と類似することになる(縦の二点透視図法ケース)。
(3) 前後方向の回転(ロール,Roll,y軸,奥行き)
たとえばY軸に30°回転するとこのようになる(他の軸は0°)。
このケースでは、もはやどの線も見かけ上、収束しないように見える。このケースでは一点透視図法と類似することになる。
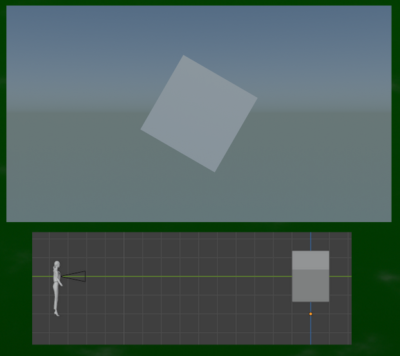
(4)水平回転(ヨー / Yaw,Z,左右に向きを変える動き)
たとえばZ軸に30°回転するとこのようになる(他の軸は0°)。
このケースは三点透視図法ではなく二点透視図法と類似することになる。
縦の消失点への収束があるかどうかがメルクマールとなる
ピッチ、ロール、ヨーという三種類の軸の回転を見てきた。このうち、対象のピッチが変わることで三点透視図法の画面になることを学んだ。
ピッチしているかどうかの指標は視心の立方体において「主に縦の消失点への収束があるかどうか」で考えることにしておく。先程のロールのケースもヨーのケースも、縦の消失点への収束がない。
観察者の視点の回転
「立方体自体の回転」をこれまでピッチ、ロール、ヨーの三種類見てきた。
「観察者の視点の回転」も同様にピッチ、ロール、ヨーの三種類に区別することができる。
たとえば立方体がピッチし、観察者の視点もピッチするというような組み合わせが考えられる。回転する/しないの単純な区別だけでも、それぞれの組み合わせは64通りある。もし回転の度数まで区別しようとしたら、何十兆もの組み合わせとなるだろう。
64通りの中で、今回我々が注意するべき組み合わせはピッチである。ここでいう三点透視図法とは、すくなくとも上下の消失点があるケースを意味する(左右に見かけ上収束しなくてもいい)。
- 立方体がピッチしていれば三点透視図法であるといえる。言い換えれば、立方体が斜めに置かれているケースである。
- 察者の視点がピッチしていれば三点透視図法であるといえる。言い換えれば、観察者が立方体を真っ直ぐではなく上下に角度を変えて見ているケースである。
図にするとこのようなイメージとなる。
暫定的な仮説
得られた暫定的な仮説は「(少なくとも見かけ上)上下の消失点へと収束するような画面を構成するためには観察者、もしくは立方体のピッチの変化を必要とする」ということになる。特定の角度の組み合わせによって例外がありうるかもしれない(検証していない)。
※回転する前は立方体は水平に置かれ、かつ水平に向いていて、観察者も真っ直ぐ見ているとする。
立方体をロールした場合の消失点はどうなるのか、という疑問が生じるがいったん保留しておく。また、ロールした立方体とロールしてない立方体が同じ画面に共在する場合、消失点はどのようになるのかという問題も保留する。
また、三点透視図法と二点透視図法が同時に一つの画面に存在する場合なども保留する。
おそらく、ロールした立方体には新たな消失点が必要になるのだろうとは仮定できる。また、新たな消失点を考えずとも、既存の消失点で立方体を作成し、そこから何らかのテクニックで回転させ、自然なロールした立方体を作成できるのだろうと仮定できる。
一点透視図法でも正面の斜線がどこにも収束していなかったことと重なる論点ではある。
また、一つの画面に複数の透視図法が存在することは原理的には可能だと仮定できるが、消失点が統一されていないと二次元化したときに、三次元では感じなかった違和感が生じる可能性がある。
人間の実際の透視図法は三点以上の、無限点透視図法とも言われることと重なる論点であり、一点や二点、三点に絞るのはその簡略化にすぎないと仮定できる。検証をとくにしていないので、仮定に留める。
三点透視図法のメリット・デメリット
三点透視図法のメリットの例
三点透視図法は「ダイナミックで爆発的な構図」を作成しやすい。
通常の一点透視図法や二点透視図法よりも、より現実に近い(多い)視界を表現できる。
たとえば対象を見る時、対象がつねに水平に置かれているとは限らず、また対象を常に真っ直ぐ見るわけでもない。
我々が生活において何かを見る場合、すこし上や下を向いているケースが多いのではないだろうか(1°でも上下すれば基本的には三点透視図法になる)。また、顔が正面を向いている場合でも、目玉を上下に動かすことはある。とはいえ、極端に「これは三点透視図法だな」とわかるような画面は日常では少ないかもしれない(少なくとも私はそうだ)。大きなビルを見上げたり、大きなビルから見下ろしたりするようなケースは私にとって非日常的である。
三点透視図法の具体例
【具体例】例えば、ビル街を見上げる構図や、高所から見下ろす視点、落下や飛翔のシーンに適している。アクションシーンやスリルを演出するのに向いており、漫画や映画、ゲームのカットシーンでも活用される。
たとえばアメコミのスパイダーマンなどはこうした視点が多そうだと推測できる。非日常的な躍動感を、日常との対比として出す場合に特に有効になりそうだ。
あらゆるシーンで極端な三点透視図法ばかりを用いていると、メリハリがつかないかもしれない。ほとんど一点透視図法や二点透視図法に画面が近いが、実質的には三点透視図法になっているケースなどもありうる(これが一番自然な気もする)。
また、作画の簡略化という理由からそうした三点透視図法を使うより、一点や二点を使ったほうが好ましいケースもあるだろう。
三点透視図法のデメリットの例
(1)写真で撮る場合の制約
・実際に三点透視図法を活かした写真を撮るには、高所からの俯瞰(ビルやドローン)、地面に近い視点での仰視(しゃがむ、寝そべる)などの環境が必要になる。
・ 一般的なカメラでは撮影が難しく、特殊なレンズや機材が求められることもある。
(2)写実的に描く場合の制約
・ 他の透視図法と違い、単にそのまま写し取ることが難しい。補助線を利用するなど、知識が必要になる。
・画面に収まる範囲や歪みの調整を意識しないと、不自然な構図になりやすい。
・物理的、肉体的な制約は写真よりも大きい。ずっと寝そべっていたり、見下ろしている必要がある。
(3)想像で描く場合の難しさ
・物理的、肉体的な制約はないものの、パースの取り方が二点透視図法や一点透視図法よりも複雑になる。また、写実するよりもより一層、知識が必要になる。
・消失点の位置が画面外に大きくずれることが多く、線を引くのに手間がかかる。漫画の場合は1からパースをつくるよりも、写真や3DCG、他のイラストなどからアタリを抽出して作る場合もある。しかし、そうした資料にプラスαで何かを描き加えたいときに、三点透視図法に関するパース知識が必要になる。
立方体以外の描画の場合の困難さ
・ 単純な立方体ではないキャラクターを描く場合、極端な遠近感の処理が難しく、バランスを取る技術が必要になる。
もっとも、(すくなくとも初心者が)パースで人間などのキャラクターを描くというのはもともと適切ではないとこの動画シリーズでは仮定している。あくまでも位置や高さ、奥行きなどのアタリ、目安を把握するための手法として活用するべきだと考えている(要するに、後はデッサンなどで自然に見える画力をつけるべきということになる)。
それゆえに、パース初心者の最終到達点は「立方体をどの透視図法でも構成できるようになること」だといえる。それ以外の球体やより複雑な形はblender(無料)などの3Dソフトで再現したほうが参考資料としても手早く、有用だろう(球体くらいならなんとかいけるかもしれないが)。
パースを学ぶ理由は参考資料の作成がメインではなく、むしろ立体感を身につける修行のような要素が大きいのではないだろうか(建築家は別かもしれないが)。
次回の予定
・三点透視図法の作成方法を学ぶ(ごく一部の方法になる)
参考文献
初心者でもわかりやすい本
ロビー・リー「超入門 マンガと図解でわかる! パース教室」
・パース全般の基礎において一冊目にこれを手に取るのに適している。 ・私は「パース!マンガでわかる遠近法」よりも平易に、かつ丁寧に説明されていると感じた。それゆえに、初心者は特に一冊目にこの本をおすすめする。
デヴィッド・チェルシー「パース!マンガでわかる遠近法
・イラストが多く、わかりやすい。パースの基礎用語の説明もされていて、かつ平易にパースの使い方が説明されている良本。ただし、建築パースに特化しているわけではなく、「イラストレーション(漫画)」に特化している点を注意する必要がある。 ・パース全般の基礎を学ぶという目的において一冊目にこれを手に取るのに適している。
上級者向け
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
絵を描く、特に線画に特化した本。小難しいが広く、深く説明されている良本。
山城義彦「現代パースの基本と実際」
・パースの歴史や細かい用語が説明されていて便利。ただしメインはイラストレーションではなく「建築パース」に特化している点を注意する必要がある。 ・かなり小難しく説明されている(建築パースゆえにそうならざるをえないのだろう)。例えるなら文系が理系の数学を見たときのあの感覚に近い。建築家ならば通らなければならない道ではある。ただし、この本はだいぶ古く、現代ではコンピューターグラフィックスをもっと多用して楽をするのだと感じた。ただし、楽をするにもその原理を知っておいて損はない。
その他
参考サイト:パースフリークス(URL)
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
・全般的な絵の知識が語られている本であり、パースに割かれる箇所は少ない。ただし、それなりにそれぞれ濃く説明されている本である。 ・パースを学ぼうとしてとる本ではないが、絵の描き方を学ぼうとする場合は選択肢に入ってくる。ただし高いのが難点。
コメント
この記事へのトラックバックはありません。

























この記事へのコメントはありません。