口(唇)の構造を分析する。口の描き方のヒント。

はじめに
- 他の前提記事について
口の構造の最小構成要素を考える
参考文献

はじめに

他の前提記事について

記事が長くなってしまい複数に分けることにしました。解剖学・構造・グリッド理論の3つに分けて多角的に口の描画を捉えていきたいと思います。今回は2つ目の「構造」です。

構造は比率ではなく、傾向のほうが近いです。グリッド理論で比率は検討していきます。なぜ陰影がつくのか？なぜそういう線になるのか？という「根拠」をすこしでもつかむ作業です。

この記事は手探りで問いを立て、仮説を立て、検証しています。わかっているものを記事にしているわけではないので正確性は保証できません。つまり、単なる思考過程のログです。

※この動画は3dcgで口を作るというものではありません。しいていえば口のアタリを分析する作業です。

絵を描くための口の解剖学知識

口の解剖学についてはこちらで説明しています。

第６回：グリッドで人間の横顔を描く方法について考える-口の描き方

側面の口についての考察はこちらです。

【blender備忘録】口をモデリングする方法のテスト①

口の3dcg制作についてはこちらで説明しています。

この記事をある程度書いて気づいたのですが、「口」の構造より「唇」の構造がメインになってしまいました。口の中の構造は表現の領域として区別することにします。また、人中や下顎等、唇の周囲の構造は別の記事で扱います。

口の構造の最小構成要素を考える

考えられる構造を挙げていきます。

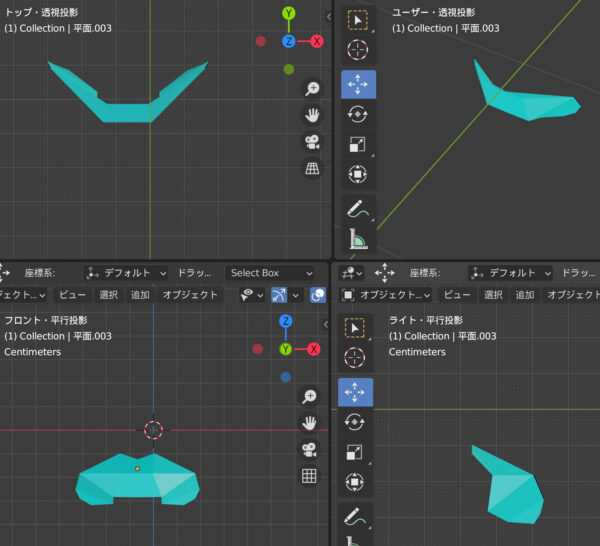
仮定1：唇はひとつの長方形とふたつの三角形で構成されている

仮説1の全体像(平行投影)

一つの長方形と、ふたつの三角形のモデルがまず考えられます。あるいはさらに分割して、二つの長方形と二つの三角形の計４つの面からなるものとして考えられます。

正面に見えるものと側面に見えるものの相違を明確に認識する

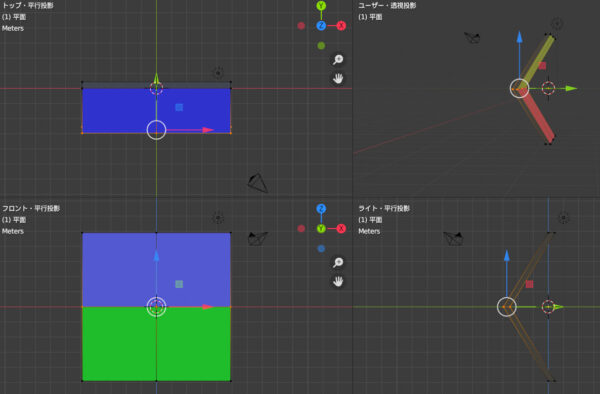
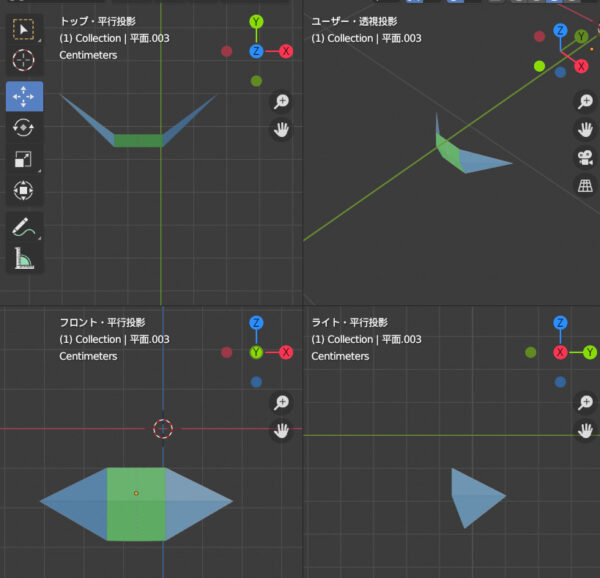
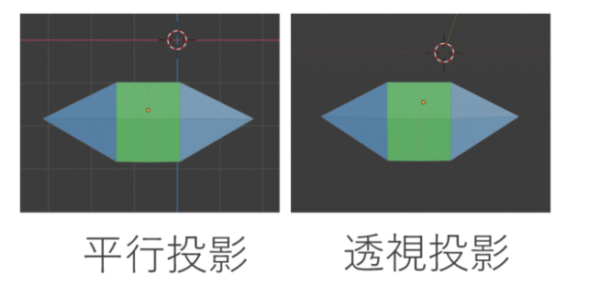
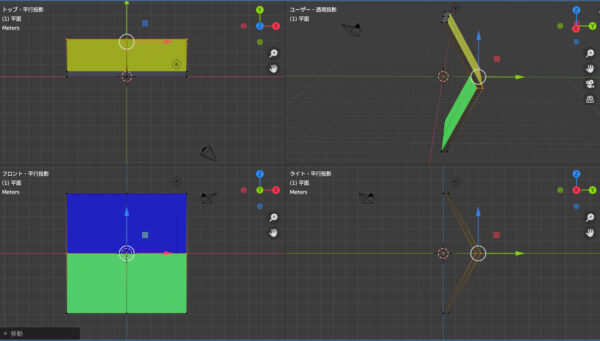
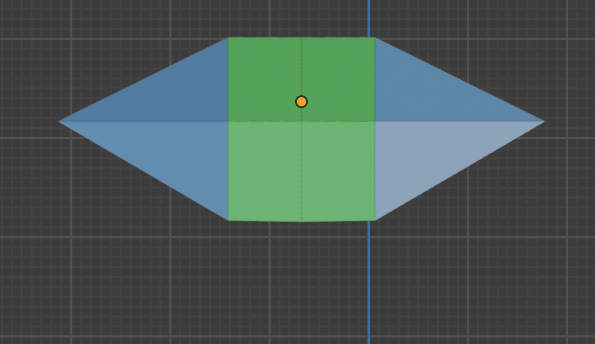
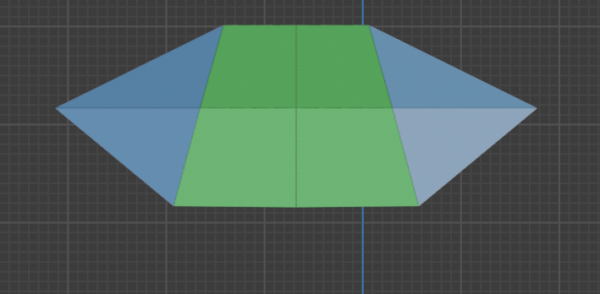
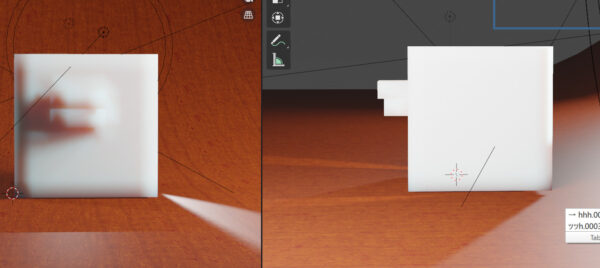
これは平行投影と透視投影を比較したものです。両者の違いが分かるでしょうか。正解は、横幅が違います。他にも細かく違うところはありますが、大事なのは「横幅」です。

動画にするとさらに明確に了解できます。

なぜこのような変化が生じるのかというと、この図形には「奥行き」があるからです。X軸とZ軸からのみ構成されていれば、このように変化しません。Y軸という奥行きの存在が、幅の広さの違いを生み出します。このようなことは遠近法の基礎理解ですが、頭でわかっても身体で覚えることがなかなか難しいです。

遠近法を単純化すれば、手前にある物ほど大きく見え、遠くにある物ほど小さく見えます。手のひらが富士山の大きさを超えて見えることもあるのと同様です。しかし実際の大きさでは富士山のほうが手のひらよりも大きいことは明らかです。すなわち、実在の問題と認識の問題が違うというのが遠近法の根本的な点です。

平行投影は「実在」をそのまま反映させる画面です。奥行きがどんなにあっても、大きさに違いを生じさせないということです。透視投影は「認識」をそのまま反映させる画面です。奥行きに違いがあれば、大きさに違いが生じます。

【絵を描くために学ぶ図法幾何学】平行投影とはなにか？

平行投影については以前記事にしたことありますので、この時点で理解できない場合はぜひご一読ください。

さて我々が漫画やイラストで絵を描くときに使うものは「透視投影」です。つまり我々人間の認識に基づいた絵を構成するのが、絵を描くということです。平行投影は実在の問題が重要になり、こうみたら4センチに見える、こうみたら10センチに見えるといったバラツキだと問題になるような「設計」の分野で使われます。例えば機械の部品の設計などです。

くの字型構造について

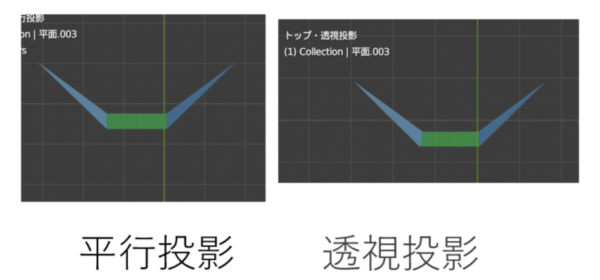
これは真上から見たものです。今度はどこが変化しているでしょうか。

こちらも動画を見ればよく分かると思います。まずは横幅が変化しています。横幅は短くなっています。つまり、全体的に小さくなっているように見えます。さらに中央の長方形は、中心に向かって斜線的になっていることが分かります。

この構成は意外と複雑ですね。真上から見ると、正面から見た時の上の長方形ではなく、下の長方形が見えているからです。

なぜそのような見え方をするのかを考えることが重要になります。

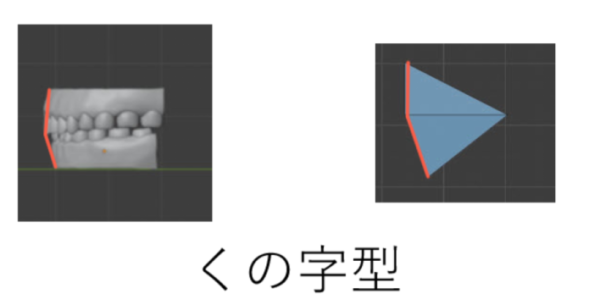
ヒントは側面図の「くの字型」にありそうです。唇の側面は、垂線的ではなく、斜線的だということです。

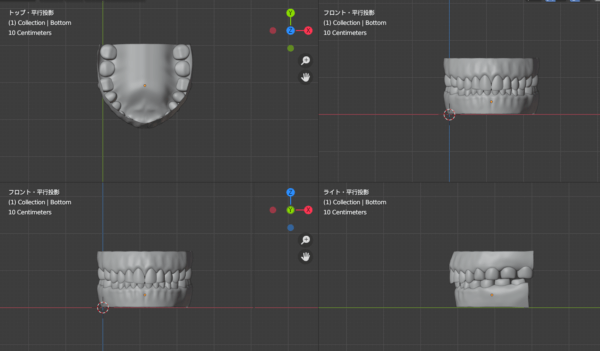
前回歯の分析をしましたが、これを見ても「くの字型」の理由がわかります。

合わせてみるとこのようなイメージになります。

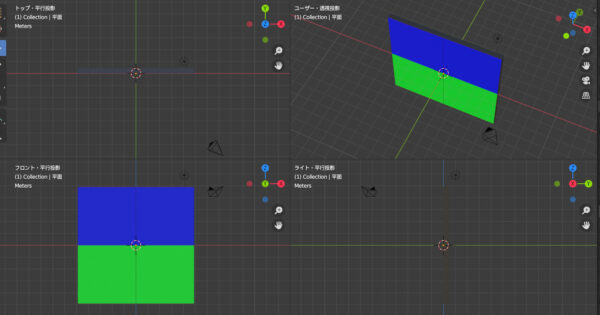
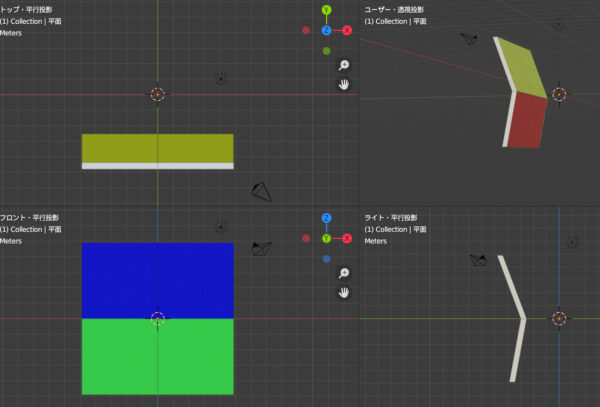
くの字型の折り紙をイメージしてください。まずは折る前の折り紙です。当然、上から見たらほとんど線にしか見えません。

くの字型に折ると、面が見えてきます。

動画にするとよく分かります。

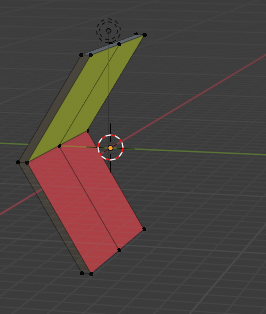
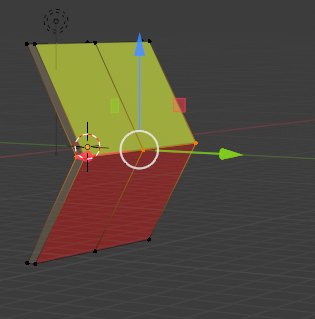
背面の黄色い部分が上から見え、前面の青い部分は隠れて見えなくなります。

口の場合は、「逆くの字」ですね。つまりこういうことです。今度は背面が隠れて、前面が見えます。ここで見える色が「赤色」ではなく「青色」ということが重要です。対照的な「くの字逆型」なら青色が見えるのです。

しかし、口の場合は上の色でいうと「赤色」の部分が見えていたということになります。

比喩的に言えば、傘が青色で、赤色を隠しているということになります。口のケースで赤色が見えなかったのは、傘が小さかったからです。

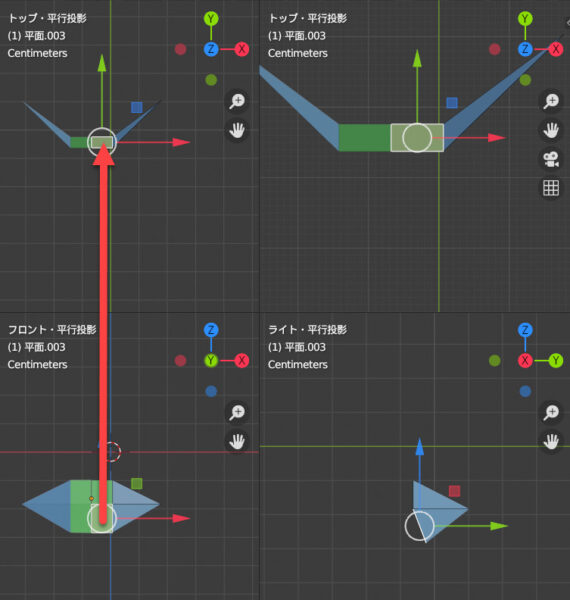
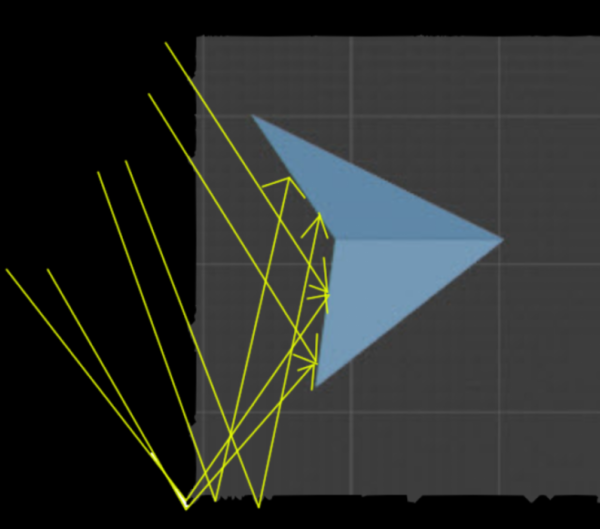
動画で表現すると、こういうことです。つまり、上半分は直線的で、下半分が斜線的な場合は、下半分の斜線的な面のみが上から見えるということですね。

つまり「逆くの字型(下半分)」といったところでしょうか。これはシンプルなモデルで起こる仮定の現象なので、これ自体が重要なのではありません。個人的に「なぜそのように認識されるのか」というのが重要なので扱いました。

さて問題は、なぜ透視投影で斜線的になるのか、ですね。おそらくこの現象は、単純に消失点へ向かって線が収束していっているからです。

この問題については別ページで扱っていますので、必要な方はご一読ください。収束していっているからこそ、近く物が大きく認識され、遠くのものが小さく認識されるのです。これは遠近感といわれるもので、この根本原則さえわかっていれば大丈夫です。

斜めに伸びる面に関する認識

さて、平行投影から透視投影に変えると横幅がなぜ短くなるかについて理解していきましょう。

これも「遠くのものが大きく見え、近くのものが小さく見える」という遠近感で説明できます。前の方で一度説明しましたが、これは「奥行き」の問題なのです。しかしどれほどの奥行きが、どれほど幅の見え方に影響を与えるか？という厳密な数値化には、厳密なパースの設定が必要になってきます。しかしこれはパースの具体論の問題なので省略します。

ここで重要なのは、口の構造において三角形の部分はY軸(奥行き)が異なるということです。そして奥行き「そのもの」を二次元において表現することはできず、”擬似”的に陰影や大小、色等々で表現きるにすぎません。どれだけ奥行きを陰影や大小で表現したとしても、モニターの奥行きは基本的に同じです。ペラペラの紙です。モニターを物理的に折れば奥行きができますが、普通に使う以上、物理的な奥行きは生じません。

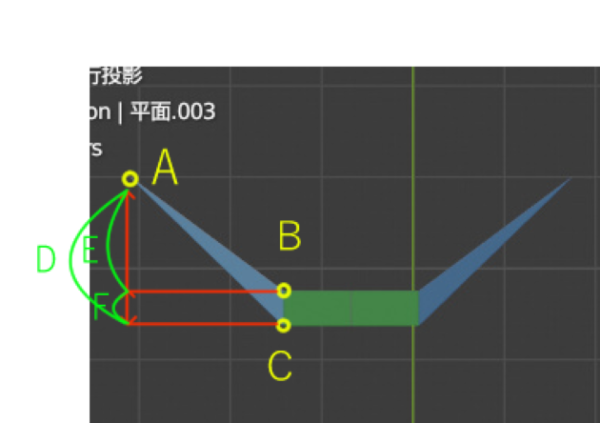
簡易的に示すとこうなります。さて奥行きはどれくらい違うのでしょうか。まず奥行きCと奥行きAの間には、距離Dほどの違いがあります。次に、奥行きBと奥行きAの間には、距離Eほどの違いがあります。奥行きCと奥行きBの間には、距離Fほどの違いがあります。奥行きCにある物体のほうが、奥行きAにある物体より「大きく」見えます。とうことは、奥行きAにある物体は「小さく」見えるということであり、X軸である幅も「短く」見えます。

この三角形は、3つの奥行きをもっているということが重要になります。このようなシンプルなモデルですら複雑なので、実際の口はもっと丸みを帯びており、何千、何万もの小さな奥行きの違いから構成されています。

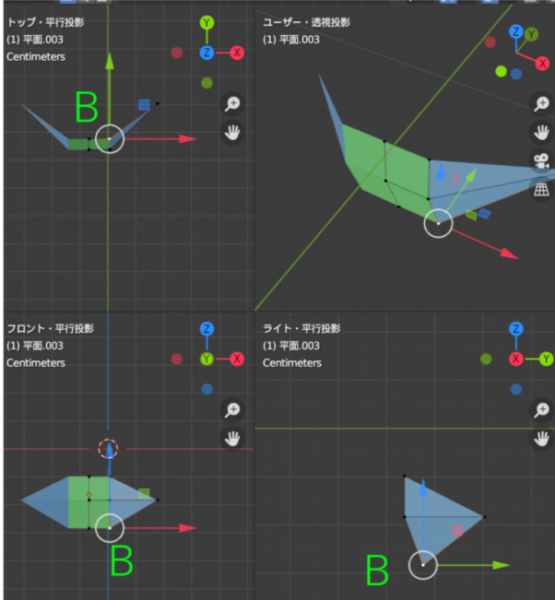上から見えていた奥行きBは、前から見ていた下の長方形の頂点なので注意してください。

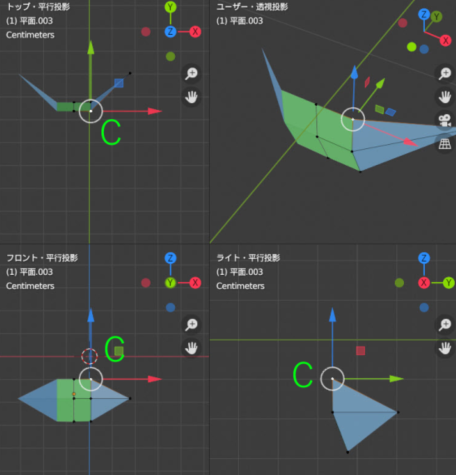さらに、上から見て「前に」見えていた頂点Cは前から見ていた上の長方形の頂点です。こうした空間の把握の理解は自転車の乗り始めは辛いものですが、慣れると自然に身についていくはずです。いわゆる「空間把握能力」です。この点は上から見るとどこに位置するのだろう、横から見るとどこに位置するのだろう、と多面的に思考できる能力は絵を描く際に役立つと思います。これは筋トレのようなものです。

もっと単純なモデルで繰り返し確認します。

実在としては同じ高さであるのにも関わらず、奥行きが違うと低く、さらに幅も短く見えます。これと同じ現象が口でも起きているということです。

つまり口の構造は顔にまとわりつくように、曲線的に張り付いているものだといえます。曲線的であるということは、奥行きを生みますよね。

逆くの字に近づける

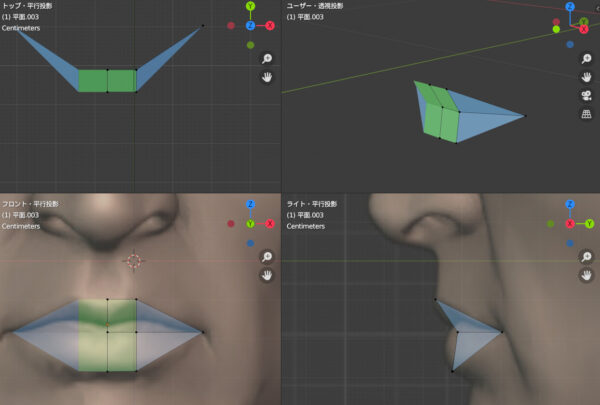
実際の顔と「平行投影」で合わせてみるとこうなります。まあまあ、わるくないですね。しかし口の「段差」があまり表現できていない気がします。

こうすれば、すこしは現実に近づくのかもしれません。つまり「逆くの字」により近づけるということです。

先程の簡易モデルで言うと、黄色い面が見えるようになるということです。

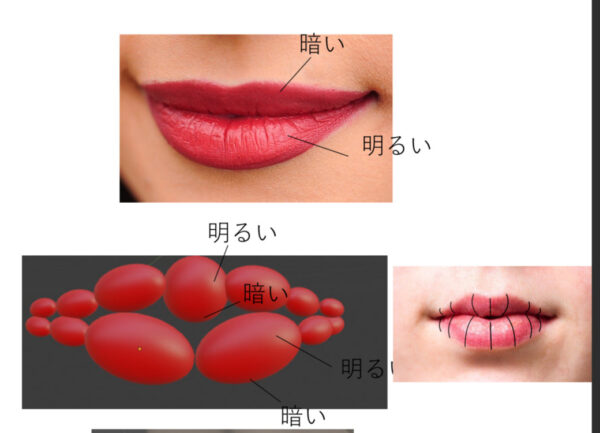
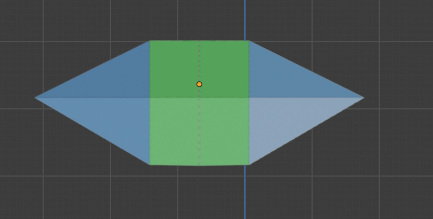このモデルの場合は、上唇のほうが下唇より「手前」にあります。つまり奥行きの違いで「段差」ができるということです。「段差」ができるということは、陰影が生じやすくなるということでもあります。通常は光源が上にあるものと想定されるので、くの字の上の面は暗くなるのです。

単純な想定を考えると、このようになります。左上に光源があると想定する場合、下の平面はより直接的に光が当たりますが、上の平面は地面に反射した光が当たる等、弱い光しかあたりません。このようなケースでは、上の平面が相対的に暗く、下の平面が相対的に明るくなります。

実際は光源や口の形状に左右される場合が多いのですが、標準的なケースを考えればやはり下の唇のほうが明るく見えやすいです。

「逆くの字」型モデルの整理

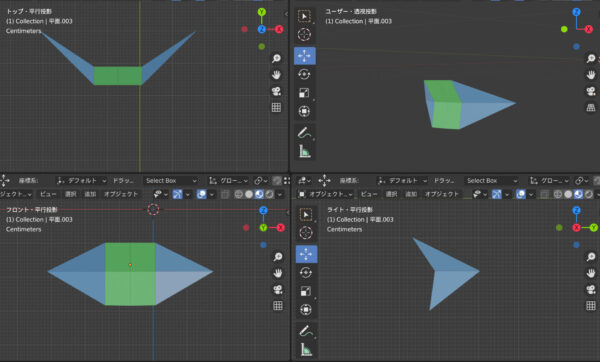
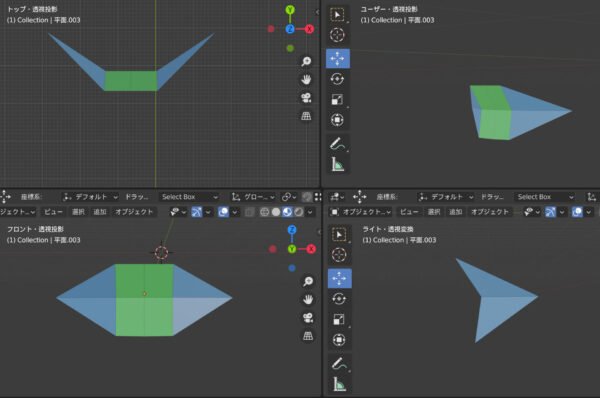
平行投影の全体像です。

透視投影の全体像です。

変化が微小なのでわかりにくいですよね。少し動画で見ていきましょう。基本的に透視投影になると幅が短くなります。上から見ると、収束へ向かって線がより斜線的になります。横から見ると、大きく見えます。横から見るとなぜ大きく見えるんでしょうか。近いものが大きく見えるので、大きく見えるのだと思います。見えていないだけで、反対側はより小さく見えています。

球体モデル

唇の描画で使われる球体

出典

こちらも球体的に唇を考えています。

出典

こちらはもっと素晴らしく、3つの球体から構成しようとしています。

球体の構造について

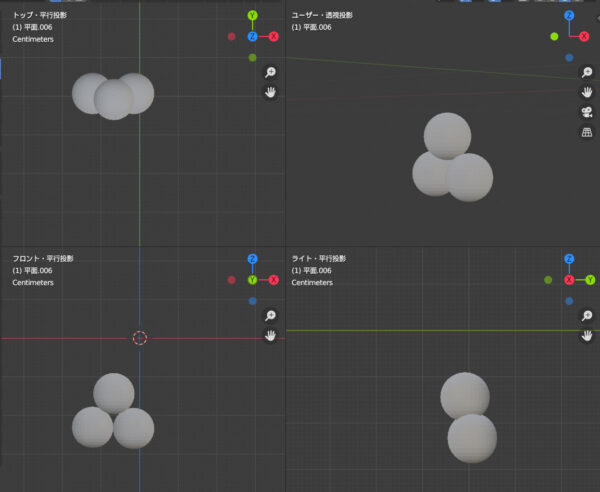
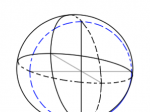
まず同じような大きさの球体がこのように並んでいることを想定してみます。

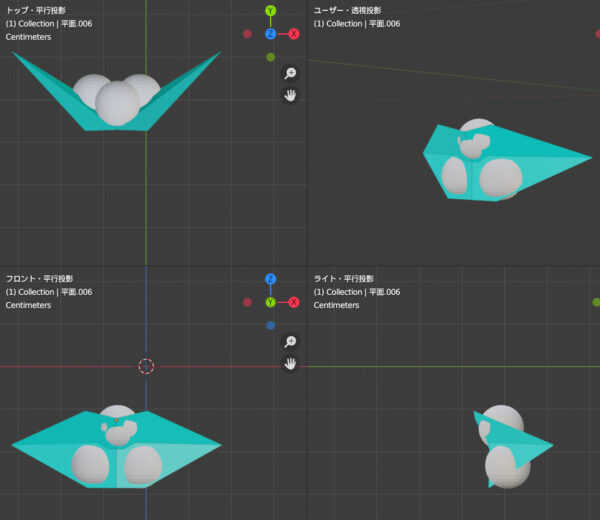
この球体状に沿って面を構成すると、このような形になります。さきほどの「逆くの字」モデルに足りなかった丸みを表現することが可能になります。

当てはめると、このような感じですね。もちろん口の真ん中の高さなど他にも細部を考慮する点がありますが、まずは単純化したモデルを作りたいので口の中心は文字通り口の中心にあるという仮定で進みます。そうした変化の領域は個性や表現の領域とします。

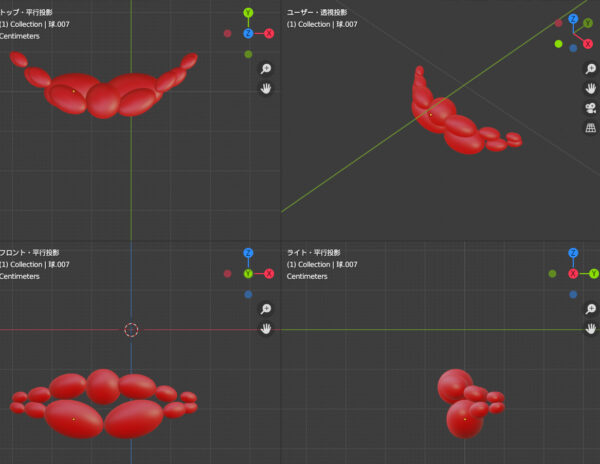
あるいはもっと球体の構造を増やして、このように考えることもできるかもしれません。

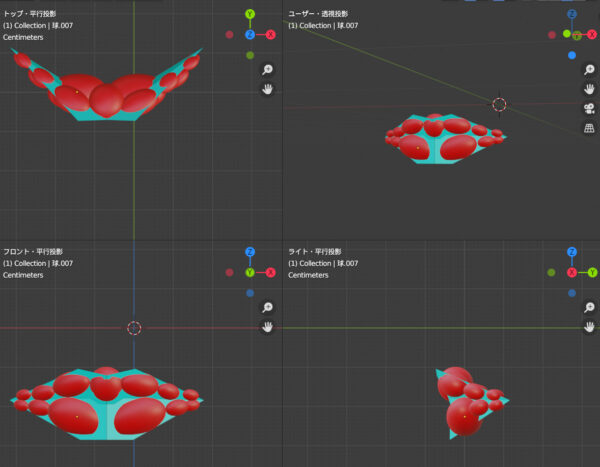
「逆くの字」モデルと合わせるとこうなります。それぞれの楕円球体は、どんどん奥へ斜め方向に配置されていきます。したがって、奥行きを生み出していく構造です。真横に並んでいるわけではないのです。仮に全ての楕円球体が同じ幅で構成されていたとしても、奥行きを生み出していく構造であれば、奥に配置された球体は手前に配置された球体よりも小さく見えるのです。小さく見えるということは、Z軸的に言えば低く、X軸的に言えば短く見えるということです。これは実在の話ではなく認識の話です。

また、仮に球体構造だと仮定すれば、球体に基づいた陰影ができることが仮定できます。あるいは「曲線」の重なりとも理解できます。球体を半分にカットすれば、そこに曲線ができます。

口の八の字構造

最初のモデルでは中央の長方形が直線的な上下関係にありました。

これを八の字型にすこし変形してみたものがこちらです。どのくらいの比率になるかは比率の問題なので、比率論で扱います。

「スカルプターの美術解剖学」

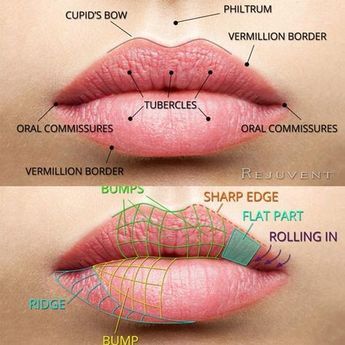
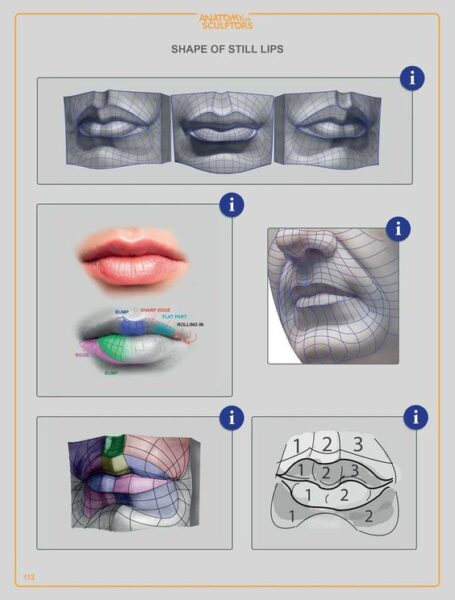
そもそもなぜ八の字型なのか、まず意識にのぼったきっかけは「スカルプターの美術解剖学」のこの説明画像です。たしかに直線ではなく八の字型のも見えます。これは口の中心から見てそれぞれ上下に最も高い「丸み」の位置を結ぶと、八の字になるという説明？だと思います。

これは透視投影です。たしかにそれぞれの頂点を結ぶと、八の字に近くなります。これは個性の領域なのか、そもそも基本性質のものなのかは定かではありませんが、一応頭に入れておいてもいいと思います。

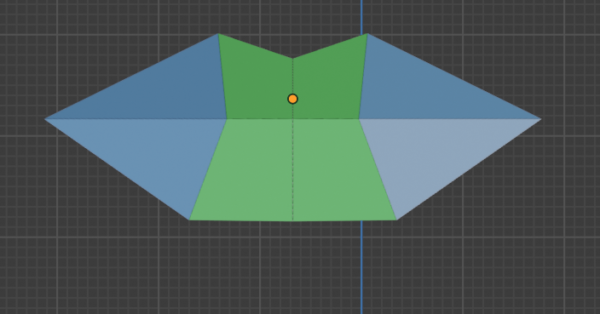とはいったものの、これは頂点同士の構造で、実際の構造はやはり「逆くの字」的であると思います。

出典

この説明イラストもとても有用だと思います。とくにFLAT PARTとROLLING INの違いは重要だと思います。つまり、唇の構造がやや斜線的な線から、端へ向かうごとにさらに曲線的な形状へ向かっているということです。

オトガイ唇溝の構造

口の真下に影ができる、というのは理解できます。なぜなら口のほうが手前にあり、口の下のほうが奥にあるからです。つまり「奥行きの差」によって「段差」ができ、陰影ができるというわけです。これは傘の理屈と同じです。傘を差せば下に影ができます。自分の唇を触れば、階段のように段差があることがわかります。

さて構造の理解で重要なのは影ができるかどうかではなく、どのような構造がどのような影を構成するのか、ということです。段差は直線的なのか、斜線的なのか、曲線的なのか、そういうものを了解する必要があります。

口の構造

「スカルプターの美術解剖学」にわかりやすく図説してありましたが、2つの構造が口の下にあることがわかります。下の１と２です、これは筋肉で言えば下唇下制筋や口角下制筋あたりなのだとおもいます。

つまり、筋肉の構造が表皮の膨らみの構造に影響を与えているということが仮説として考えられます。

それっぽいものをつくってみました。

物体Aと物体Bの間にあることにより、その隙間Cの陰影が目立つということです。

もし物体Aと物体Bがないと仮定すれば、隙間Cが目立つということはなく、唇の下全体が暗くなります。

もし物体Aと物体Bがあると仮定すれば、物体Aと物体Bのほうが手前にあり、隙間Cよりも明るくなるので、隙間Cは相対的に暗く見えます。

簡易構造的にはこうですね。この隙間Cを解剖学用語では「オトガイ唇溝(しんこう)」といいます。

もうすこしわかりやすくライティングするとこのようになるでしょうか。さらに物体Cとして「顎(あご)」が手前に出てくるので、その三者に挟まれる形になります。

イチョウが向かい合っているような構造ですね。

ネガとポジの関係のように、あるものの形態は「それ以外の形態」によっても定義できます。たとえば顎の丸みがあるから、オトガイ唇溝の周囲も丸みがつく、というように了解することもできます。

口の中心の線はなぜ線に見えるのか？

これはシンプルに「奥行きの段差」によって陰影が生じるからだといえます。

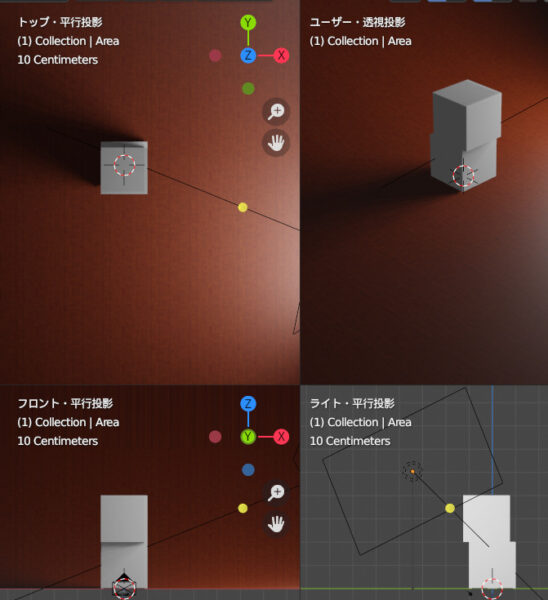たとえば立方体を2つ縦に並べ、すこし奥行きをずらしただけでその境界線に影ができます。

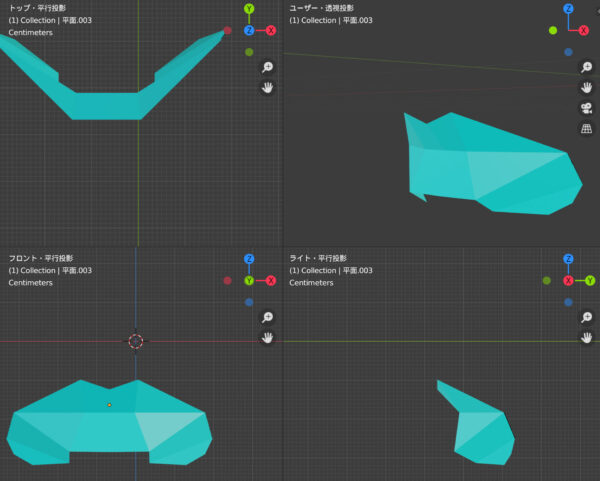そしてこの影の構造は口の線の構造と類似しています。もし仮に唇の真正面に強い光を様々な方向から当てると、影がなくなって線が消えます。あるいは暗闇の中でも同様に線が消えます。線は色と同様に、光に依存する現象だと言えます。

口角、モダイオラス、ほうれい線の区別と整理

すごく頭がごちゃごちゃしています。というより理解している人は少ないはず。

それぞれの定義をざっくり振り返りましょう。

口角(こうかく)：上唇と下唇がつながっている部分。口の両わきの上下のくちびるが合う部分。くちわき。
モダイオラス(口角結節)：蝸牛軸、あるいは口角結節とも。ラテン語のハブに由来する。口角近くに付着している多くの絡み合う筋で作られた結合組織構造。表面から見ると唇の両端の小さな肉の山。陰影と明暗により小さな皮膚のつまみのようにみえる
ほうれい線：ヒトの鼻の両脇から唇の両端に伸びる2本の線。しわでは無く、頬の境界線である。鼻唇溝。
マリオネットライン：口角が下がることによって現れる垂直ラインのこと。頬のむくみやたるみ、片側だけで噛むクセなどが原因に

モダイオラスと口角

このへんになってくるとよくわからないんですよね正直。

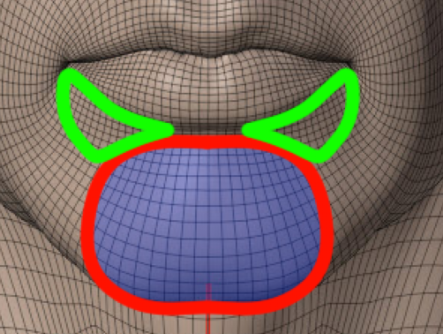
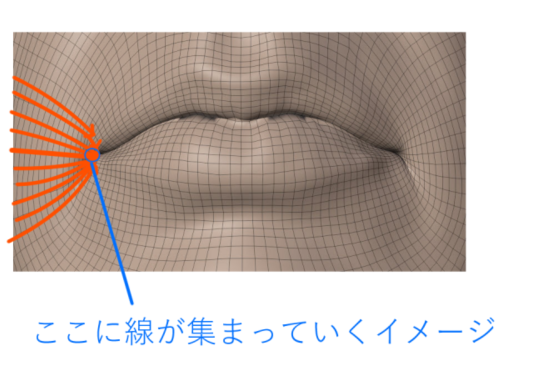
モダイオラスについては線の集まりというイメージです。実際に解剖学的にもさまざまな筋肉が集まる位置です。

脂肪や筋肉など、さまざまな要素の「境目」としての構造といったらいいのでしょうか。しかし描画においてそうした構造の理解をどう活かせばいいのかが明瞭としません。

そもそも口角とモダイオラスを分けて考えるのか、セットで考えるか悩みます。隣り合わせなので、お互いに関連付けしあっているような気がします。

©集英社、奥浩哉

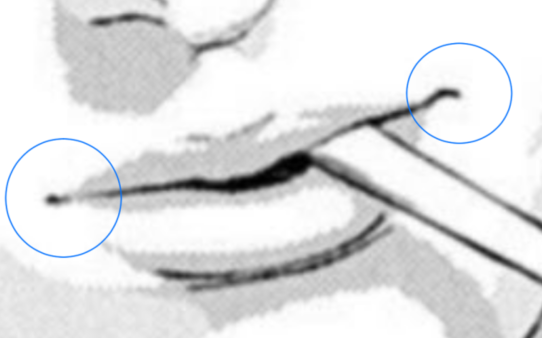
この二次元の描写でもモダイオラスが表現されています。

つまり、唇の中心の線の「端」がいわゆる口角＋モダイオラスなわけです。これを線としてどのように表現するか、というのがポイントになります。すこし太い線、あるいはすこしの斜線とでもいうのでしょうか。線があるからには、そこに段差があるということをこれまで学んできました。

まず奥行きとしては深い「点に近い口角」があり、さらにその横の「モダイオラスのふくらみ」が上下にむかって「線的なシワ」を構成しているとでもいえばいいのでしょうか。

「スカルプターの美術解剖学２」

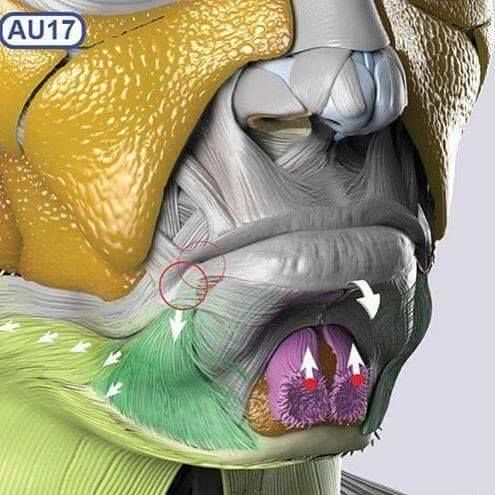
一番わかり易いのは「スカルプターの美術解剖学２」のこの画像なのですが、それでも正直よくわからない。たしかに筋肉が集まる位置にモダイオラスができる、つまり口角に筋肉が結節するということは理解できる。しかしこれを見ると、溝のようなものが膨らみの中にさらにあるような気もする。しかし気のせいかもしれない。

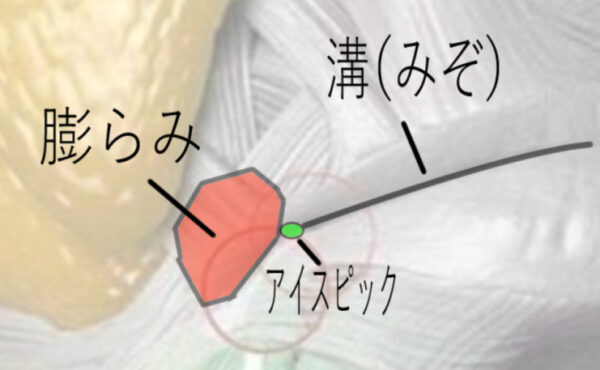
私のいままでのイメージでは、こうです。つまり、膨らみの凸、アイスピックとしての深い凹、線的な溝としてのやや浅い凹の合わさったものとして、口の線画が構成されているのではないか、ということです。

たとえば平面に突然凸があれば影ができます。

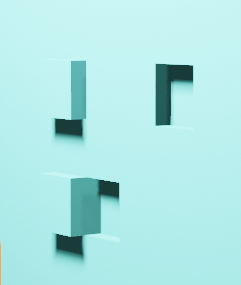もし凸と凹が隣り合わせの場合は、凸だけの場合よりも段差が広がります。たとえば１と０の差の絶対値は１ですが、１と－１の絶対値は２です。段差としては２倍になっています。

つまり、筋肉が集まってくる膨らみである凸と、口の隙間である凹が隣り合わせになり、その相乗効果として段差の絶対値が増え、影として目立っているのではないか、という仮説です。単純に上唇と下唇の間に段差ができていて、前提として線があります。そこに膨らみの効果が重なり、さらに濃い線ができるということです。それが口角＋モダイオラスという仮説です。

だからなんだと言われたらこちらは沈黙せざるを得ませんが、とりあえず記憶の肉付けにはなりそうです。

＜水戸場所＞千代丸の顔を変形させる、嘉風。#sumo pic.twitter.com/gRBXWmPeIm
— 日本相撲協会公式 (@sumokyokai) April 24, 2015

たとえばこうした表情におけるモダイオラスはどうなっているのか？などと考えてみます。これは単純に頬の肉が中央に押し出され、さらに凸が大きくなり、段差がさらに増え、線として大きくなったのではないでしょうか。モダイオラスはどこへいったのか、正直わかりません。モダイオラスかもしれませんね。これはおそらく表現の領域なので、今回は深く扱いません。スカルプターの美術解剖学２あたりで記載されているかもしれません。

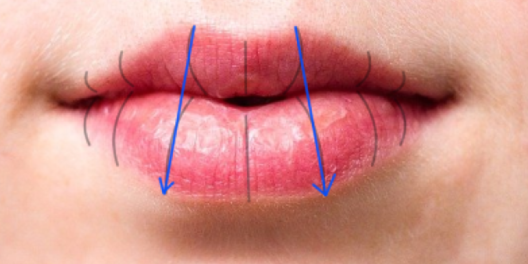
ちなみにこれがマリオネットラインです。高齢な方によくでるようです。笑顔になると、ほうれい線とモダイオラスとマリオネットラインがすべて一致しているような線にみえますね。

出典

たとえばこの引用させていただいた画像を見てください。どこが口角でどこがモダイオラスでしょうか。

出典

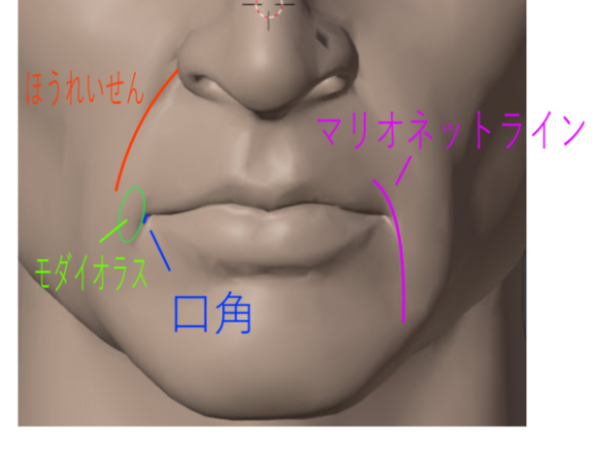
あるいはこの説明を見てください。ほうれい線とマリオネットラインの区別がよくわかります。

参考文献

人体の描き方関連

やさしい人物画

ルーミスさんの本です。はじめて手にした参考書なので、バイブル的な感じがあります。

人体のデッサン技法
ジャック・ハムも同時期に手に入れましたが、比率で考えるという手法にルーミス同様に感動した覚えがあります。ルーミスとは違う切り口で顔の描き方を学べます。

一番オススメの文献です。３Dのオブジェクトを元に作られているのでかなり正確です。顔に特化しているので、顔の筋肉や脂肪の構造がよくわかります。文章よりイラストの割合のほうが圧倒的に多いです。驚いたときはどのような筋肉構造になるか、笑ったときはどのような筋肉構造になるかなどを専門的に学べることができ、イラスト作成においても重要な資料になります。

アーティストのための美術解剖学

こちらはほとんどアナログでイラストがつくられています。どれも素晴らしいイラストで、わかりやすいです。文章が少し専門的で、難しい印象があります。先程紹介したスカルプターのための美術解剖学よりも説明のための文章量が圧倒的に多く、得られる知識も多いです。併用したほうがいいのかもしれません。