顔の立体性・割合(プロポーション)・法則・透視図法に関する研究(第二回)
目次
頭部を面で構成してみる
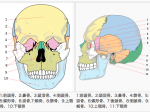
1:頭部の面の把握(ルーミス編)
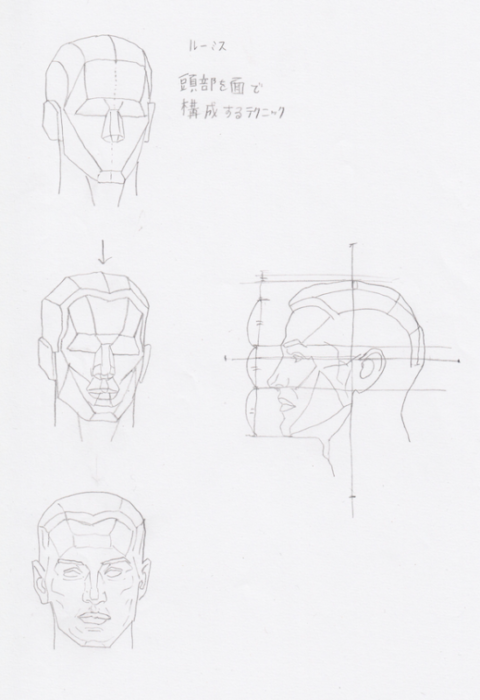
頭部の各面を覚えることはとても重要です。こうした面を覚えることによって、明暗をつけながら頭部を表現する基礎を把握できるようになるからです。記憶できるように練習してみましょう。
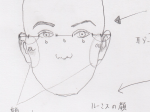
遠近法を使った頭部の理解
遠近法と顔のイメージ
なんとなくのイメージです
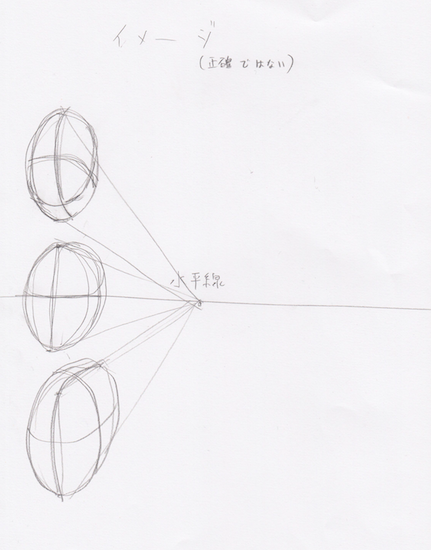
ルーミスさんを参考にしました。

これは顔をどの視点で、どの高さで描くかによって描き方がかわるということです。水平線の位置がちょうどこの絵における視点ですね。
2:そもそも遠近法って何?
遠近法は大体理解しているつもりだったのですが、いざ描いてみるとなかなか息詰まることがあります。もう一度詳しく学んでみようと思います。今回はスコット・ロバートソンの『HOW TO DRAW』とデヴィッド・チェルシーの『パース!マンガでわかる遠近法』をもとに学んでいこうと思います。
| 遠近法(perspective):ボリュームや空間関係を平面上に表現する手法 |
人間の視覚をそっくりそのまま紙の上に創りだすことはできないそうです。カメラもその意味では同じではないでしょうか。立体としてそのまま再現するのではなく、立体のよう「見せかける」テクニックが遠近法であるといえます。
3:(遠近法の理解)水平線って何?
| 水平線(horizon line) :画面を横切る水平方向の線。この線の位置が観察者の視高(アイレベル)と一致する。 |
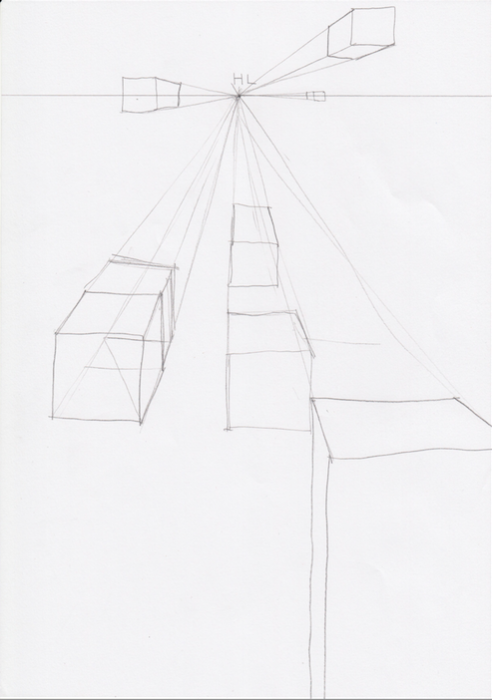
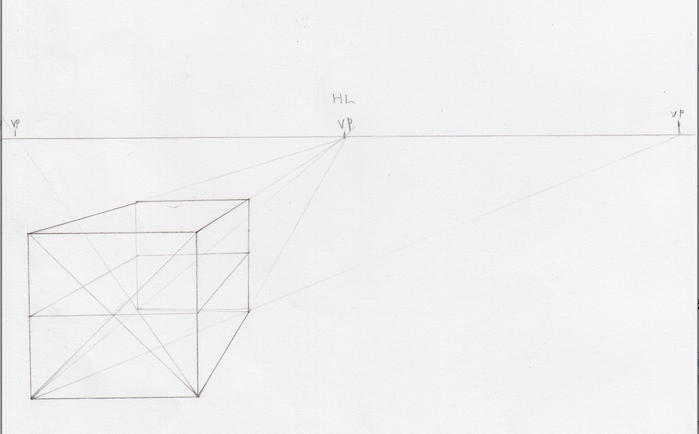
実際に絵で説明してみます。HLが水平線です。Horizon Lineの頭文字をとったものがHLです。HLが高い順に並べてみます。ラフですが、一点透視図法です。一点透視図法の説明は後ほど行います。
水平線は目の高さに保たれています。マグ本によると、水平線は空間にフラフープを置いたみたいなものだといいます。絵を描く側が高くジャンプしたり、飛行機で高い位置に移動すれば、当然水平線の位置も高くなります。低くしゃがめば、水平線の位置も低くなります。
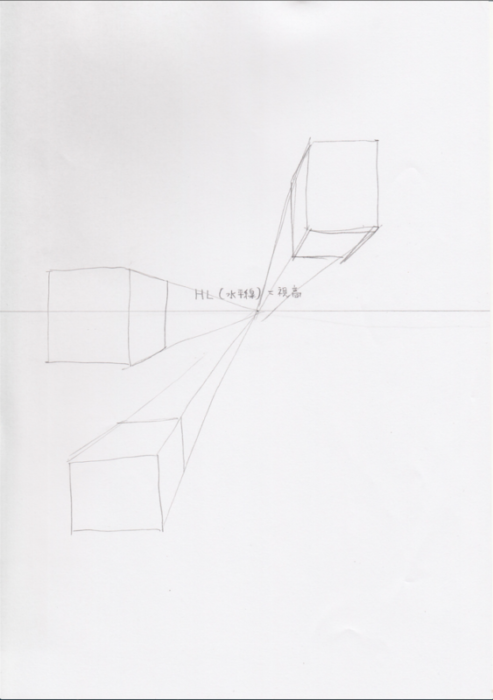
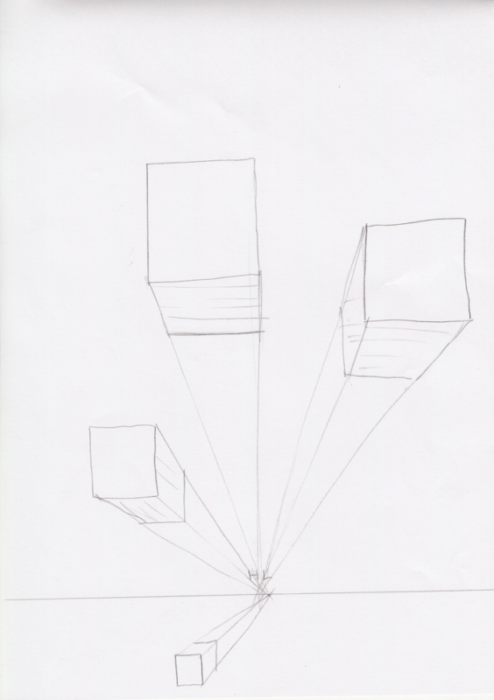
4:(遠近法の理解)一点透視図法って何?
一点透視図法:遠近法の一種で消失点を1つ持つ構図。奥行き方向の線は全て消失点に収束するように放射状になる(実用日本語表現辞典)。 消失点(vanishing point):通称VP。画面の奥へ向かう平行線が収束していくように見える点。 対角線の消失点:同じ幅の立方体をつくるために今回は対角線の消失点を使います。 |
消失点が一つしかない透視図法ですね。まずは描いてみます。先ほどの水平線(HL)と、今回学んだ消失点(VP)を組み合わせて一点透視図法を構成します。本当は視円錐についても触れなければいけないのですが、今回か頭部の立体性の記事なので、省略します。次回の記事で視円錐を詳しく扱います。
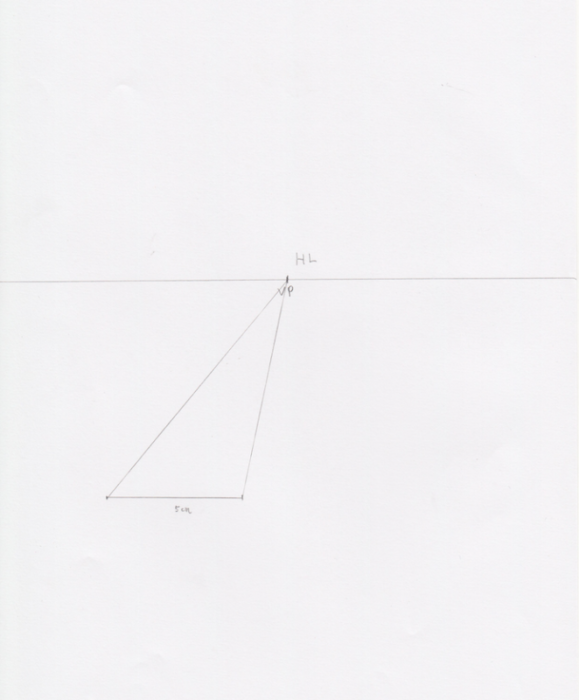
まずはHLとVPを設定します。次に、任意の位置に直線を引きます。今回は5cmにしました。

次に、引いた線からVPに向かって線を伸ばします。
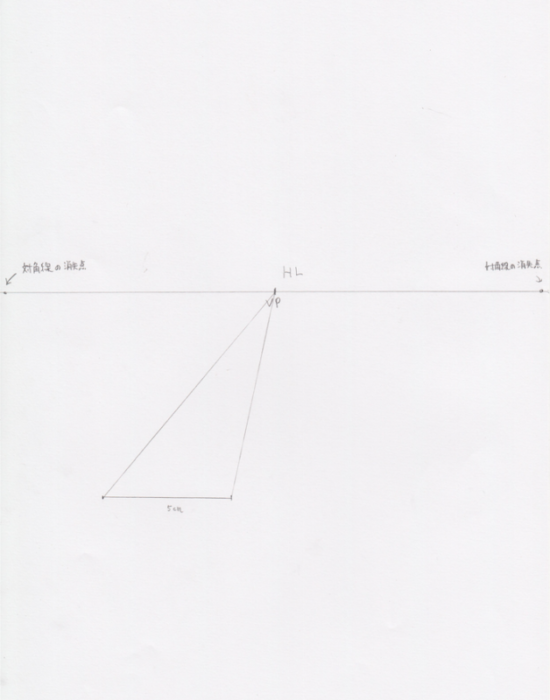
今は幅の線が5cmです。幅が等しい立方体を描くとき、一点透視図法では高さも定規では買った時と同じ5cmになります。しかし、奥行きの高さや幅は当然実寸通りの5cmではありません。どのようにその幅を決めるのかというと、「対角線の消失点」というものできめます。この消失点はどの位置でもいいのですが、できるだけ離れたほうが歪みにくいです。本来ならばもっと離れていてもいいです。詳しいことはパースの記事で扱います。視円錐などとも関係してきます。
引いた線から対角線の消失点へ向かって線を引きます。最初にVPに向かって引いた線をクロスするような位置が、奥行き5cmの幅になります。実際に測ると紙の上では3cmや3cmですが、5cmなのです。これが「トリック」なのです。もし定規で5cm通りに奥行きを書いてしまうと、歪んでしまうのです。
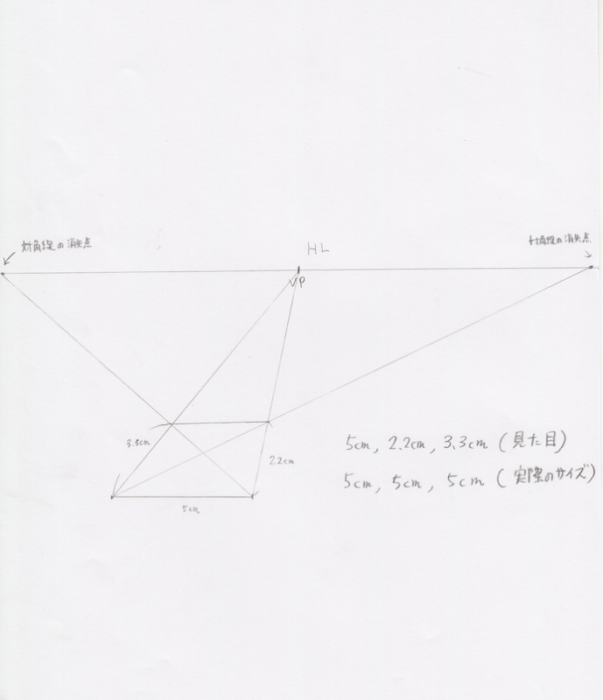
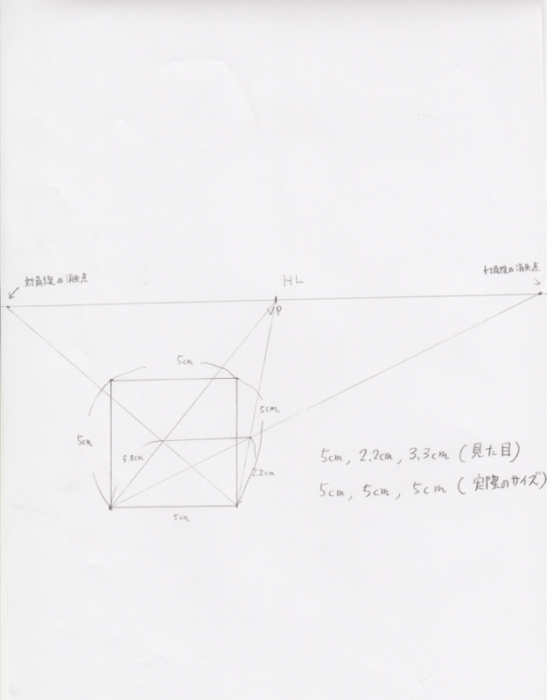
後は同じようにVPへ線を伸ばしたり、するだけです。簡単な作業です。これで5cmの立方体が完成しました。
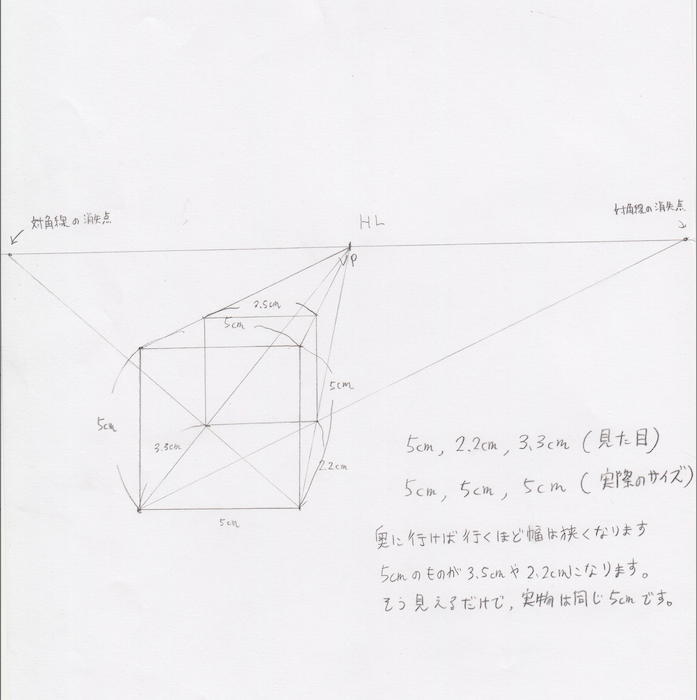
これが顔の立体性とどのように関係するのか。それはこの立方体から球体を構築すればおのずと答えは見えてきます。
5:(遠近法の理解)透視図法と頭部の立体性の関係とは?
まずは立方体を四分割してみます。今回は新しく作りました。線は薄くしたほうがいいかもしれません。
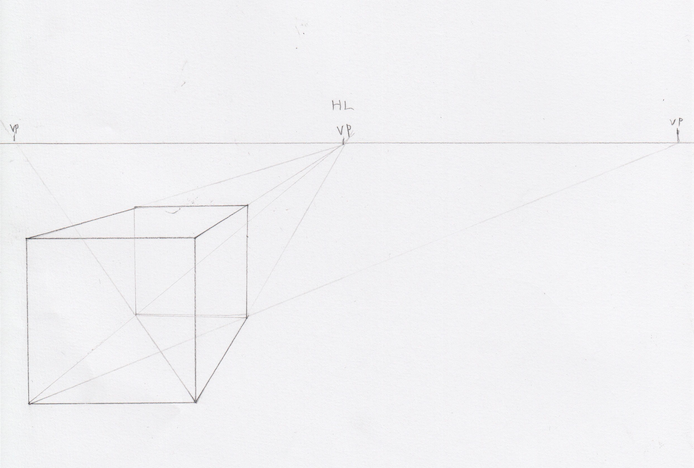
バツ印をクロスさせると、その面の半分の位置がわかります。
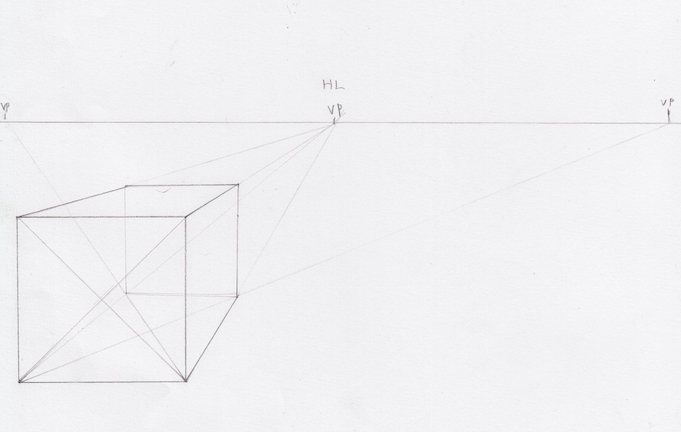
この手順ですべての面を4分割します。
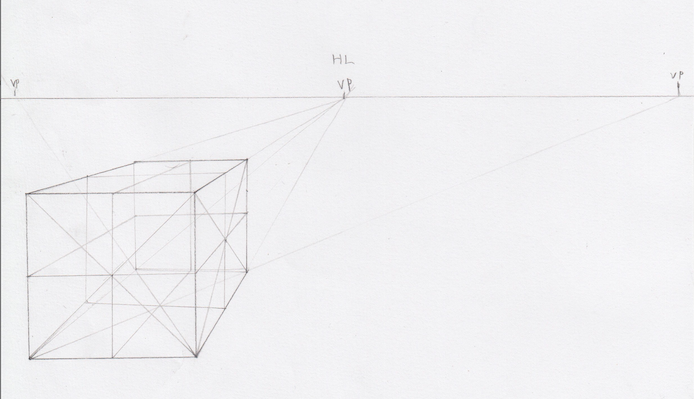
これで立方体は完成です(したのほう少し曲がっちゃった(´;ω;`))。
これを元に、球をなんとなくかきます。
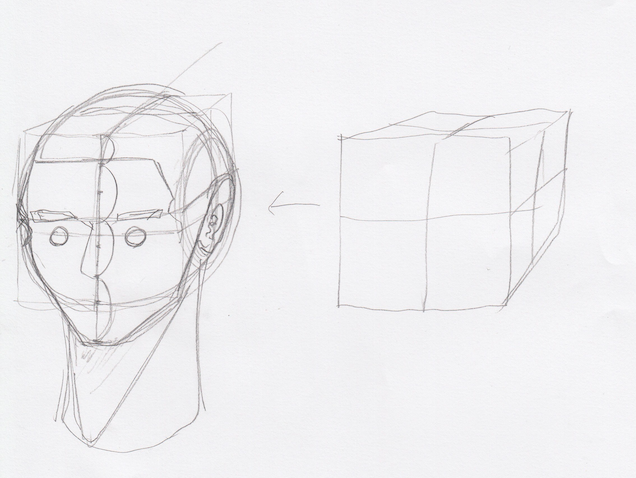
イメージ的にはこうなります(これでいいのか?)。
なんとなく球体の線の位置が把握できるようになったと思います。つぎに、立方体から球体をどのようにつくるかについて研究してみたいと思います。
6:立体とアウトラインの関係
すべての立方体には3つの寸法があるといいます。長さ、幅、厚さの3つです。それを元に立方体を構成します。
どうやらX,Y,Z座標というものも関係してくるらしいです。ロバートソンによれば、透視図を描くには、XYZ座標系を理解しないといけないそうです。X、Y、Zで定義される空間では、3つのじくがいずれも消失点に向かっています。それぞれの軸と垂直に交わる平面をそれぞれ、X平面、Y平面、Z平面と呼ぶそうです、どの平面上に描いているのかを常に意識し、描画をしっかりコントロールすることが重要です。
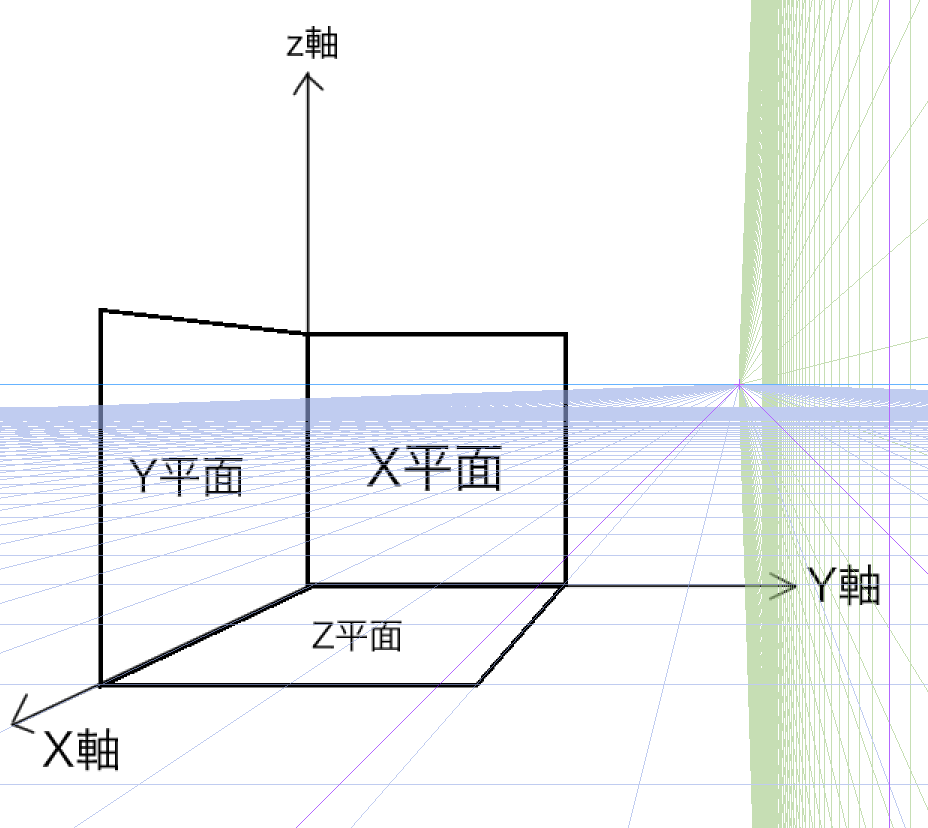
球体を描く実験をしてみます。失敗したらごめんなさい。まずは円をXYZ平面に書いてみます。
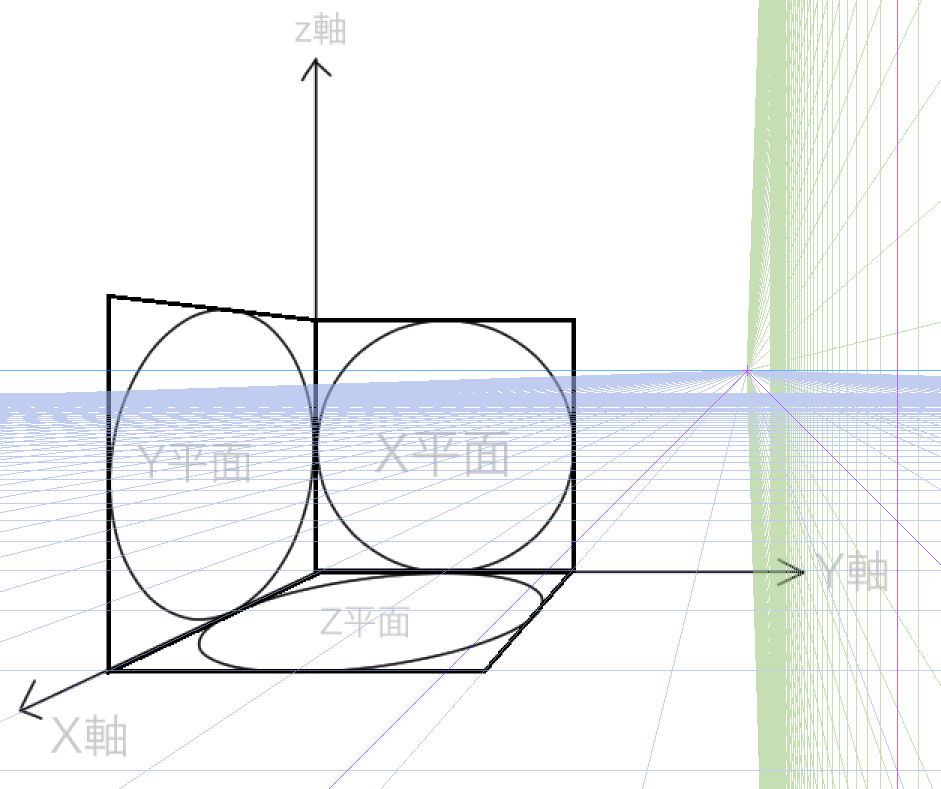
そこから四角形を4分割します。
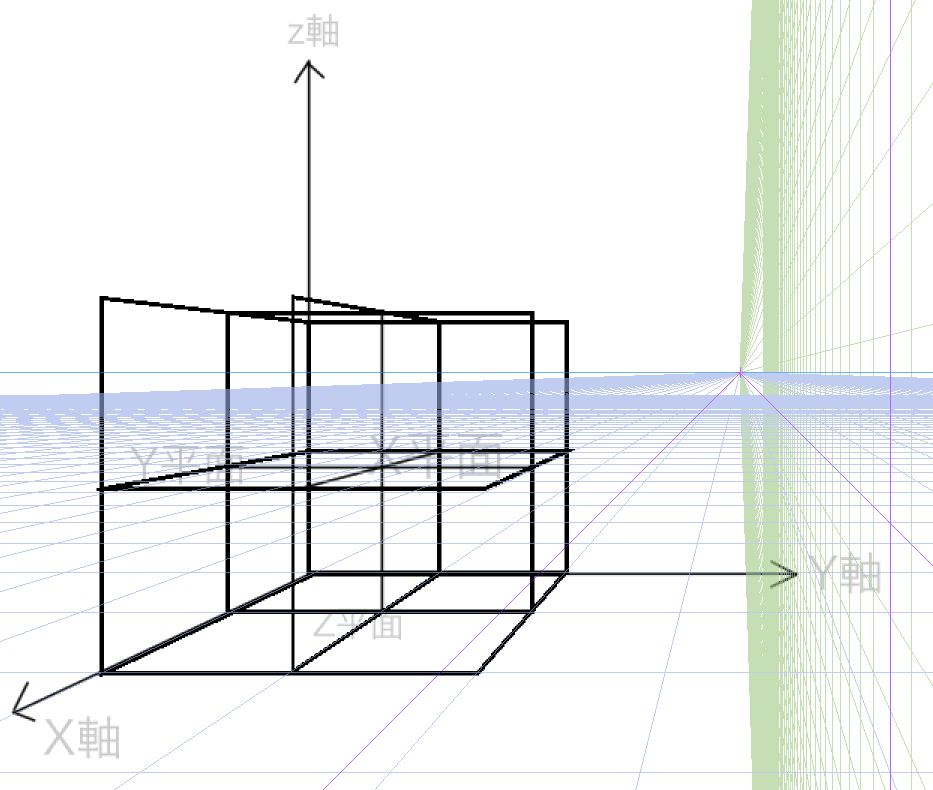
分割した箇所に円を描きます
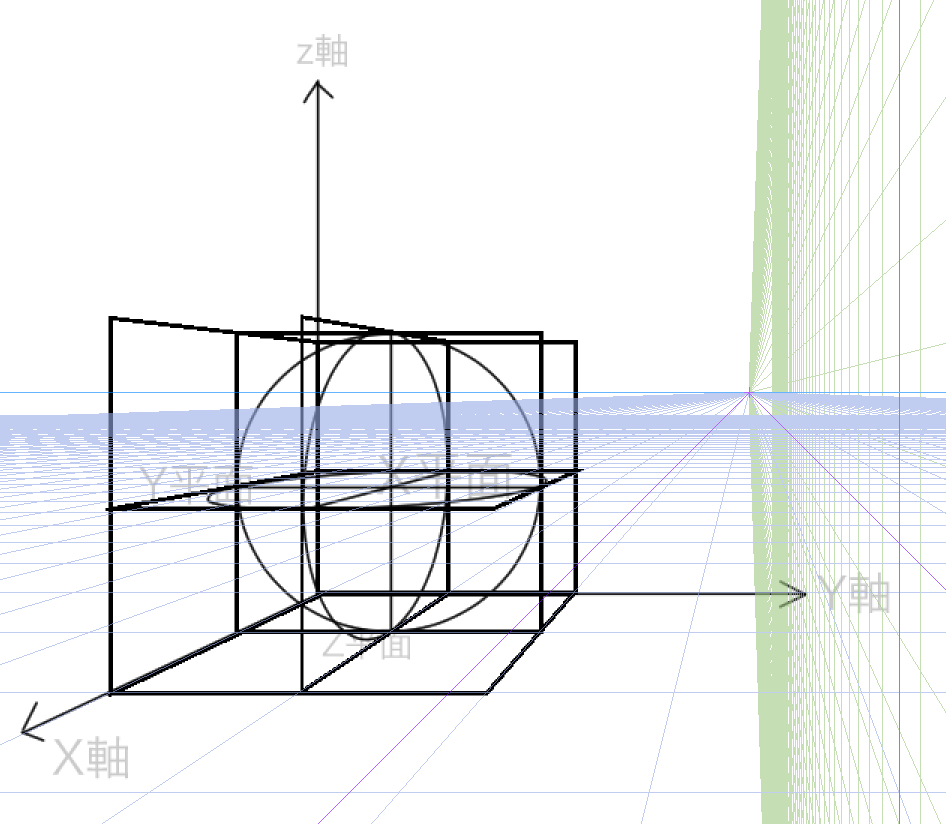
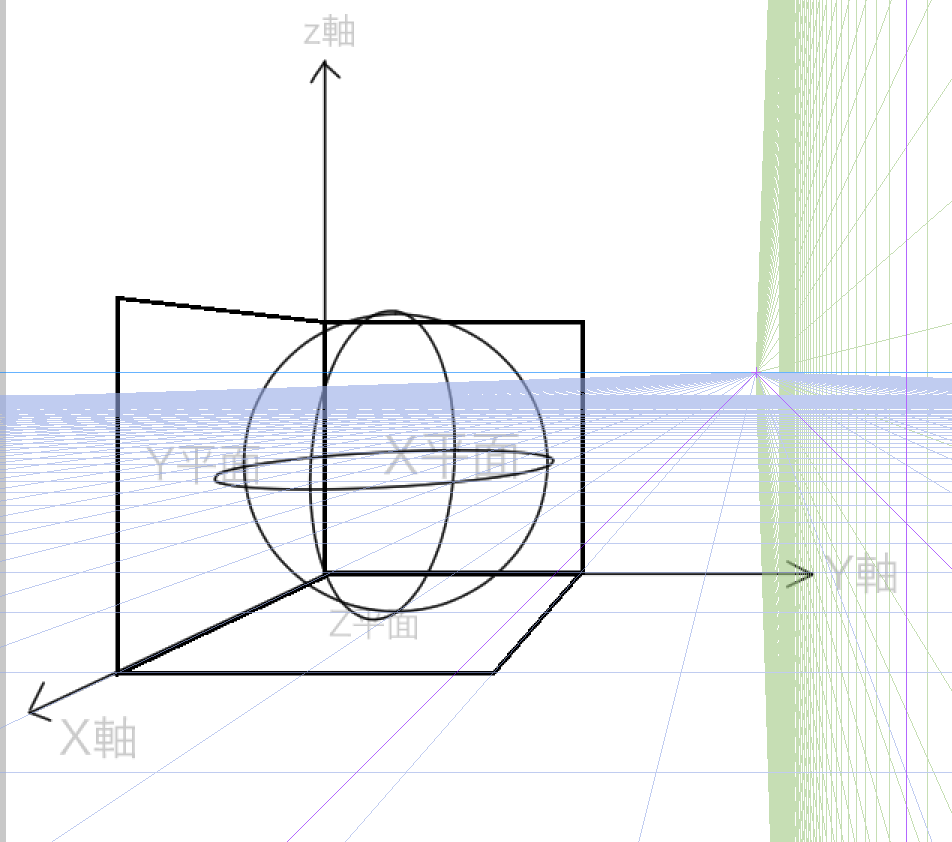
問題はここからです。微妙にずれていますよね。たしかにボックスの半分の位置を使って球体を描くと、このようになります。綺麗な球体を描く方法はないのか・・と模索している状態です。元の線を青く固定して、ベクターレイヤーをつかってすこし円の大きさを変えてみたものがこちらです。
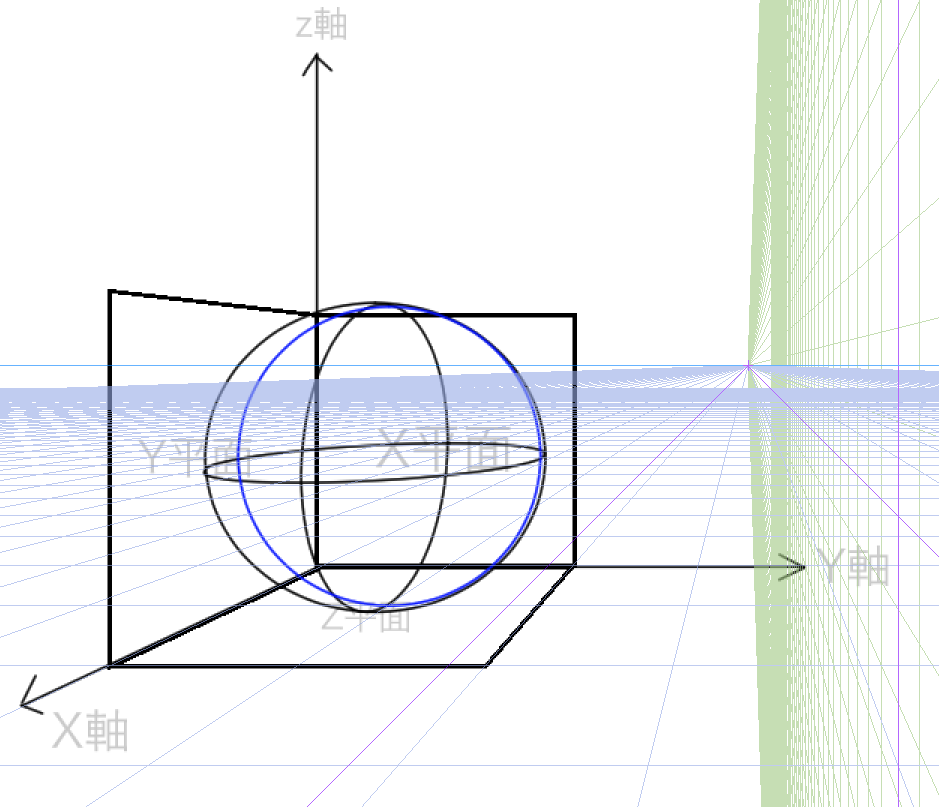
青い線がちょうど球体の半分の位置、4分割の位置だとしたら、新たにつけたした黒い線は、実際に見える球体の線であるといえます。
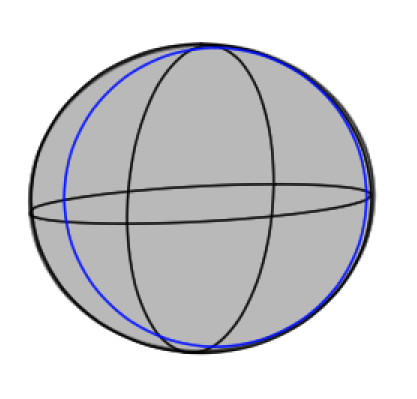
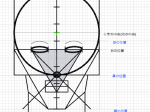
これを次は正面から描いてみます。
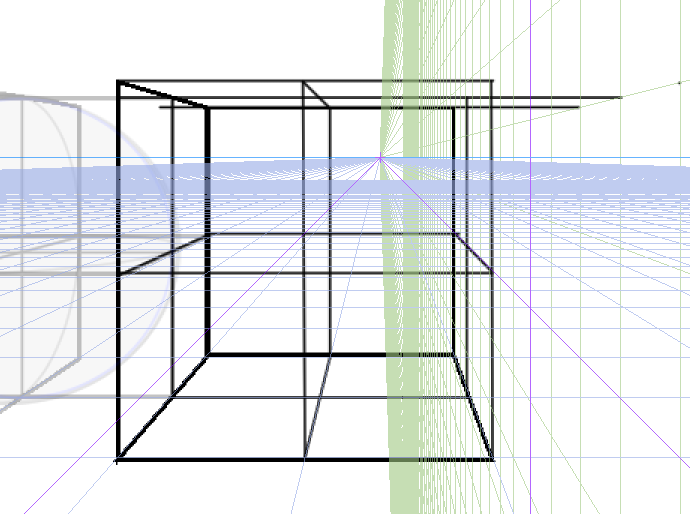
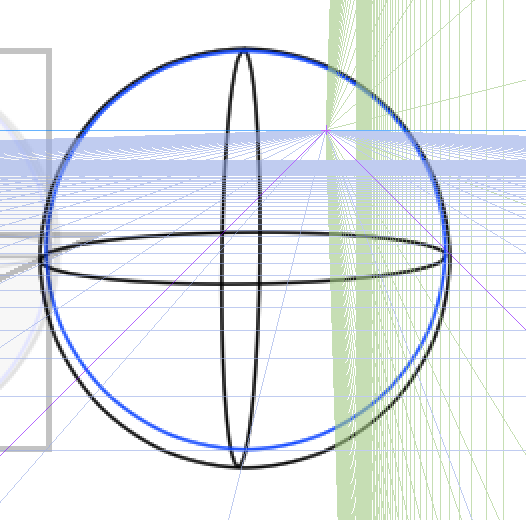
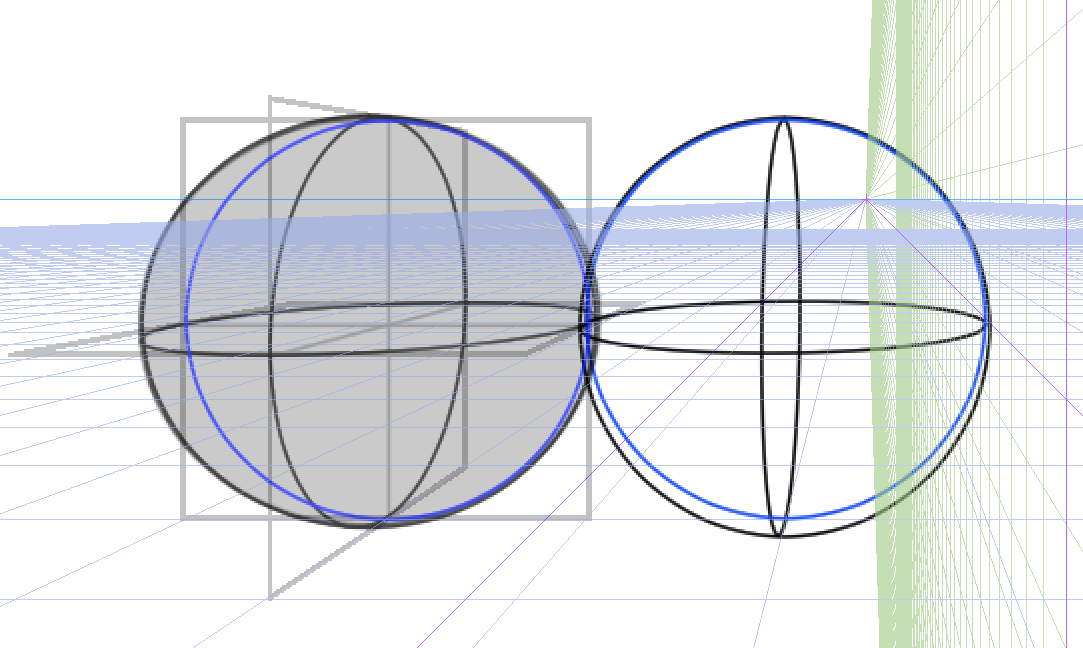
上にも描いてみましょうか。
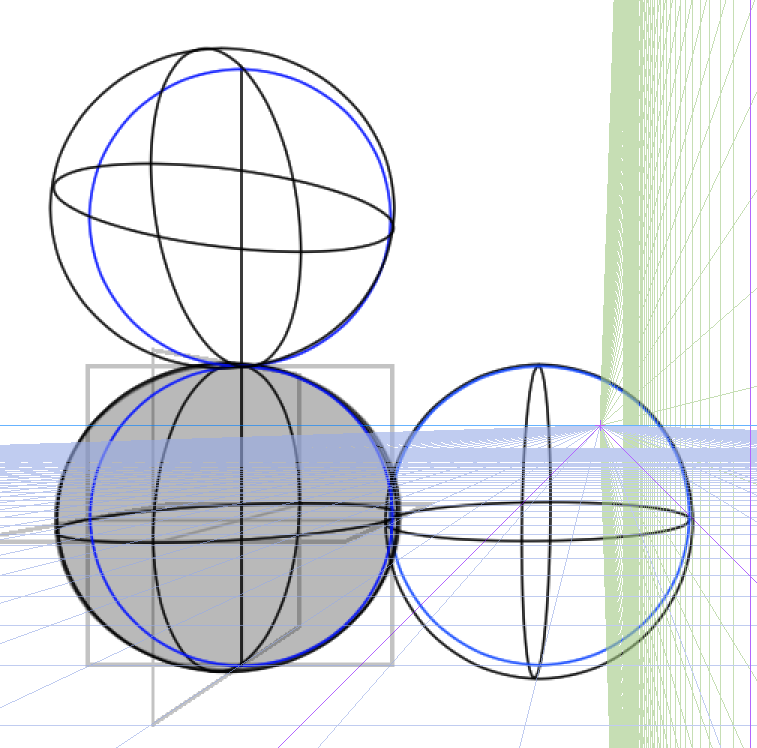
正確に見える線だけを描くと、このようになります。
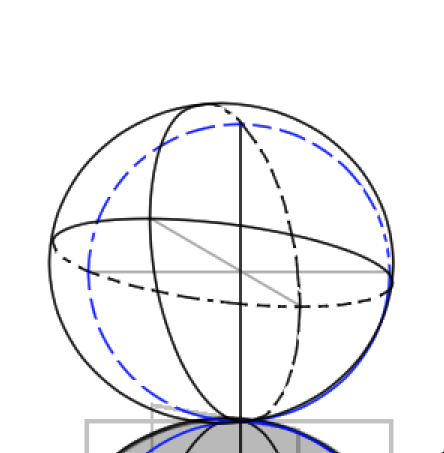
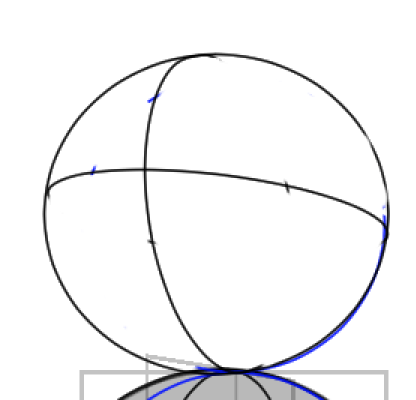
コメント
この記事へのトラックバックはありません。









この記事へのコメントはありません。