目次
- はじめに
- 対角線の消失点を割り出す関数一覧(是非ブックマークしてください)
- 【部分】45度のDPの位置を割り出す(正方形の場合)
- 【部分】50度のDPの位置を割り出す(正方形の場合)
- 【部分】60度のDPの位置を割り出す(正方形の場合)
- 【全体】45度のDPの位置を割り出す(正方形の場合)
- 【全体】50度のDPの位置を割り出す(正方形の場合)
- 【全体】60度のDPの位置を割り出す(正方形の場合)
- 【全体】45度のDPの位置を割り出す(長方形の場合)
- 【全体】50度のDPの位置を割り出す(長方形の場合)
- 【全体】60度のDPの位置を割り出す(長方形の場合)
- 【部分】45度のDPの位置を割り出す(長方形の場合)
- 【部分】50度のDPの位置を割り出す(長方形の場合)
- 【部分】60度のDPの位置を割り出す(長方形の場合)
- パースにおける視円錐を理解する
- 参考文献
はじめに
動画での説明
・この記事の「概要・要約・要旨・まとめ」はyoutubeの動画の冒頭にありますのでぜひ参照してください。
よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m
対角線の消失点を割り出す関数一覧(是非ブックマークしてください)
【部分】45度のDPの位置を割り出す(正方形の場合)
【部分】50度のDPの位置を割り出す(正方形の場合)
【部分】60度のDPの位置を割り出す(正方形の場合)
【全体】45度のDPの位置を割り出す(正方形の場合)
【全体】50度のDPの位置を割り出す(正方形の場合)
【全体】60度のDPの位置を割り出す(正方形の場合)
【全体】45度のDPの位置を割り出す(長方形の場合)
【全体】50度のDPの位置を割り出す(長方形の場合)
【全体】60度のDPの位置を割り出す(長方形の場合)
【部分】45度のDPの位置を割り出す(長方形の場合)
【部分】50度のDPの位置を割り出す(長方形の場合)
【部分】60度のDPの位置を割り出す(長方形の場合)
パースにおける視円錐を理解する
視野と視円錐の違い
視野とはなにか、意味、定義、わかりやすく解説
前回の動画(第三回)で説明したように、大きな画面である視野と、特定の画面であるキャンバス(ファインダー)に分けて画面を考えることができる。
視野角とはなにか、意味、定義、わかりやすく解説
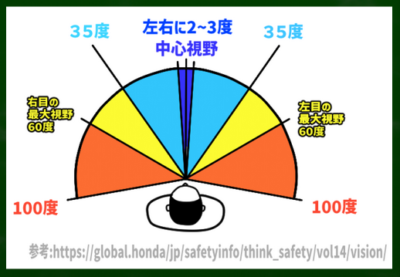
視野角:目やカメラが一度に見ることができる範囲を角度で表したもの。
人間の視野角のうち、最大視野は100度、有効視野は左右に35度程度くらいだといわれる。いわゆる有効視野が自然に見える範囲の境界あたりである。パースの世界では左右に30度ほどだともいわれる(視円錐60度)。
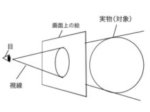
視円錐とはなにか、意味、定義、わかりやすく解説
視円錐(Cone of Vision、COV):透視図法において、観察者が自然に見ることができる視界の範囲を示す概念のこと。線画によって示される視覚領域のこと。視野角と同義的に扱われることもある。
要するに、視円錐とは視野や視野角の範囲の中で人間が特に自然に見える範囲を角度で表し、それをさらに円錐の形で図示したものだと言える。特定の画面はこの自然に見える視界の範囲にできるだけ合わせて構成する必要がある。
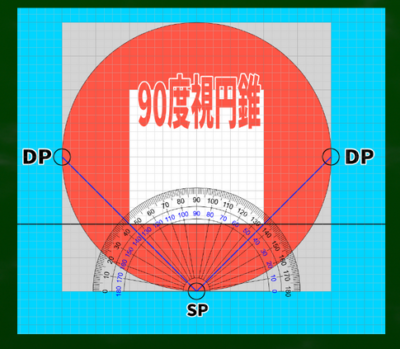
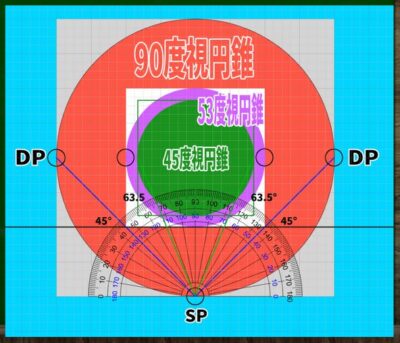
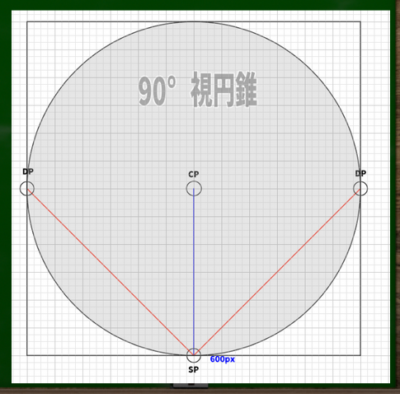
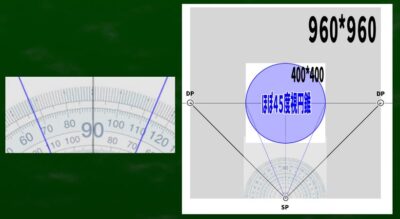
たとえば以前作成した対角線45度の距離点(DP)を用いた90度の視円錐は、このような形で図示することができる。
左右に45度ずつであり、180-(45*2)=90であるため、90度の視円錐ということになる。
前回の動画の勘違いについて
幅の長さと視円錐の大きさは単純な比例か?
どこか間違っていると思いつつ、どこが間違っているのかがよく理解できなかった点について今回は掘り下げていこうと思う。
前回の動画をまるごと消すことも考えたが、私の動画はそもそも正解を陳列する講座ではなく「理解の履歴(ログ)」であるため、失敗もまた成功の元と考えていく。私と同じ失敗をする人への助けにもなるはずである。
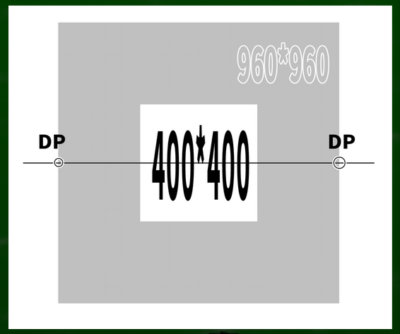
私の認識では、正方形のキャンバスの場合、45度の対角線の消失点の幅の半分のキャンパスが45度の視円錐にぴったり収まるものだと考えていた。
つまり、幅の長さと視円錐の大きさが比例すると考えていたのである。たとえば800の幅が90度視円錐を形作るならば、400の幅が45度視円錐を形作るものだと考えていた。ここが私の勘違いだ。
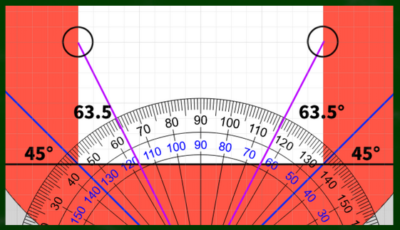
しかし実際に分度器を使って線を引くと、視円錐が45度にはならないことがわかった。
だいぶ昔に同じことを実験したことがあるのだが、分度器がたまたま合わないという都合の良い解釈をしてしまっていたようだ。
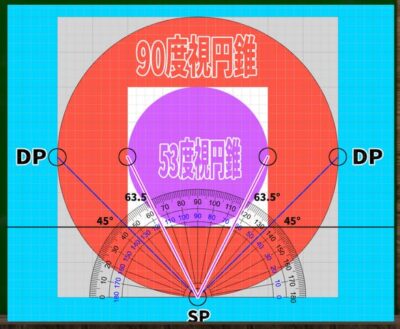
実際の視円錐は45度ではなくおよそ53度
実際に得られたデータはおよそ63.5度であった。
180-(63.5*2)=53なので、およそ53度の視円錐が400*400のキャンバスと重なっていることになる。
もちろん、視円錐は一般に60度未満なら歪みは小さいのでこれでも大きな問題はない。実際に立方体を作成しても、大きな歪みは見られなかった。
ただし、一点透視図法では50度未満40度以上が推奨されることがあり、わずかに大きいことになってしまうので個人的に気になってしまう。
今回の動画では、この400*400の画面にちょうど45度の視円錐(他にも50や60)がぴったり重なる方法があるかどうかを模索していくことになる。
45度の視円錐が画面に収まる位置を探す
45度の視円錐はどのあたりにあるか
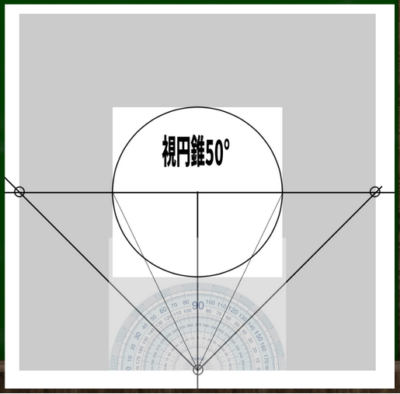
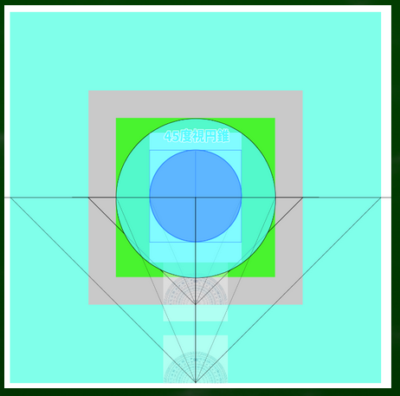
45度の視円錐はどのあたりにあるか、分度器を使って作成してみた。
この緑の円と画面(白い部分)がぴったり収まるようにするにはどうしたらいいのか。
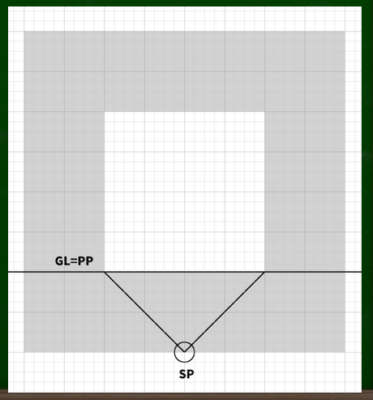
前回はこのように、GL(基線)とPP(画面)が等しい位置から、45度に線を伸ばしてSP(立点)の位置を決めていた。
そこから線を伸ばして対角線の消失点を見つけていたのである。ただし、前回の対角線の消失点の位置が間違っていたというわけではない。
対角線の消失点の位置は正しく、それを利用して歪みのない立方体を描くという目的ならば、おおよそ成功している。
画面からではなく、立点から考えてみる
すこし発想を変えて物事を捉え直してみる。前回はキャンバスの大きさありきで、立点の位置を決めていた。今回は立点の位置を自由に決めてみよう。
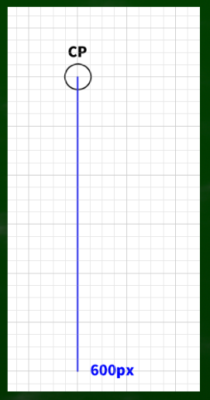
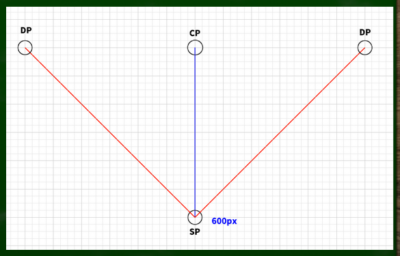
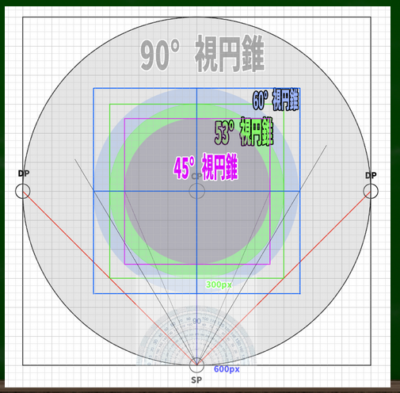
まずはCP(視心)からの距離である。この距離を任意に決め、今回は600Pixelだと仮定する。そうすると、このようになる。肝心なのは、まだ画面(PP)のサイズを決定していないという点である。45度の視円錐ができたら、そこに画面をつくればいいものとする。
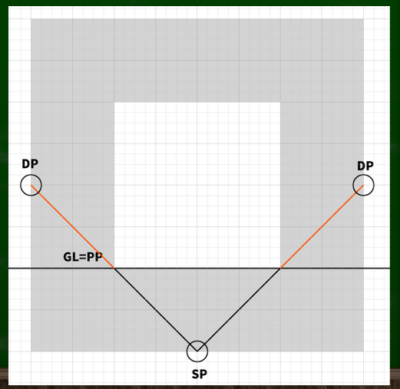
このCPからSP(立点)の距離によってDP(対角線の消失点)の位置が決まる。
SP(立点)から45度の線を伸ばし、CP(視心)の線上、つまりIL(アイレベル)の線上に重なる位置がDP(対角線の消失点)となる。
CP(視心)からDP(対角線の消失点)、もしくはCP(視心)からSP(立点)の位置を基準に正方形を作り、そこに円を描くと90度の視円錐ができる。
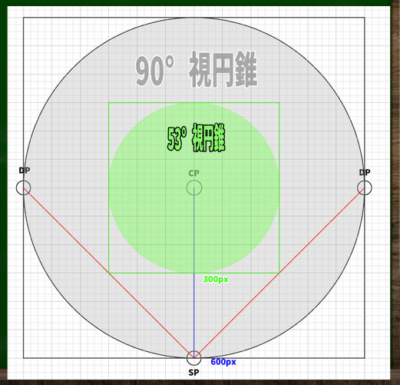
次に、適切な視野角、つまり視円錐内に画面を収める必要がある。
先ほど計算した通り、CP(視心)からSP(立点)への距離を半分にすると、約53度の視円錐が形成される。
しかしわれわれは、この距離の半分の画面以外を今回は作りたい。しかも45度の視円錐にぴったりおさまる画面(キャンバス)を作りたいとする。
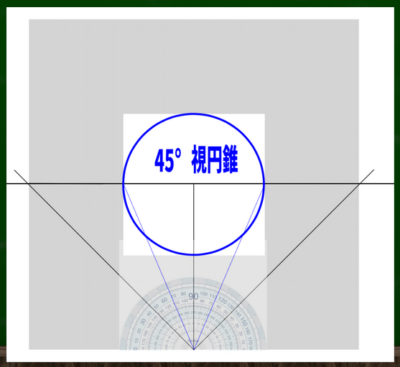
(1)分度器を使って画面を構成する方法
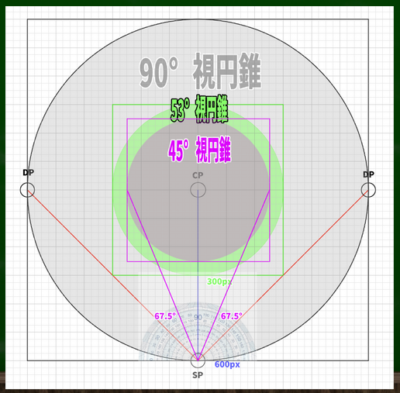
【1】まず、素直に分度器を使う方法がある。左右に67.5度の線をSP(立点)からIL(アイレベル)線上にのばしていけばいい。
これで45度視円錐ができるので、これを覆うような正方形を画面として後から設定すればいいのである。たとえばここから500*500ピクセルにキャンバスを設定すればいい。
キャンバスサイズを使って画面を構成する方法
【2】分度器以外の方法を探す(キャンバスサイズを使う)
- CP(視心)からSP(立点)までの距離は600である。
- 90度の視円錐は1200*1200である。
- 53度の視円錐は600*600である。
- 45度の視円錐は500*500である。※数字はおおよその数値で厳密ではない。
どうにかしてキャンパスサイズのみから、45度の対角線の消失点内にぴったりおさめたい場合はどうすればいいのか。
まず考えられるのは、「SP(立点)の距離を伸ばす」というアイデアである。つまり、PP(画面)ではなくDP(対角線の消失点)の位置を調整するということである。
500*500がPP(画面)のときに、DP(対角線の消失点)は1200にくる。つまり、およそ2.4倍の位置に来ると仮定することが出来る。
この法則を応用させると、400*400がPPのときには、400*2.4=960の位置にDP(対角線の消失点)が来ると推測することが出来る。
具体例:400*400のキャンバス内に45°視円錐を作る方法
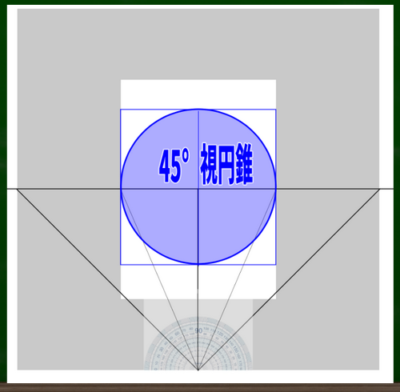
試しに作ってみよう。まずは400*400のキャンバスをつくる。
次に、960*960をつくり、そこをDP(対角線の消失点)とする。
このPP(400*400の画面、絵を描きたい画面)がちょうど45度の視円錐に収まっているかどうか、分度器で測ってみる。
その結果、左右に67.5度の直線上近くに一致した(誤差はありうる)。つまり、45度の視円錐に収まっているということである。
180-(67.5*2)=45
まとめると、正方形のキャンバスに限っては、
・45度DP=HもしくはW×2.4となる。
・53度DP=HもしくはW×2となる。
他にも汎用性が高そうな、40度、50度、そして1点透視図法ではあまり使わないかもしれないが60度も計算式を出していくことにする。
※Hは高さ、Wは幅を意味する。特定の画面内の正方形に収まる正円の任意の視円錐を出したい場合の式である。
50度の視円錐が画面に収まる位置を探す
50度の視円錐を構成するための数式を探す
50度の視円錐はおおよそ576*576だった。したがって、1200/576=2.083…である。繰り上げて2.1とする。建築でもない限り、単位の厳密な正確さは不要だと考える。
・正方形のキャンバスに限っては、50度DP=HもしくはW×2.1となる。
50度DP=HもしくはW×2.1を前提に、画面を構成していく。H(W)を400とする。計算すると、およそ840になる。
この位置にDPを設定していく。そうすると、おおよそ正しい位置、つまり50度視円錐が画面にくる位置にきた(左右に65度)。
60度の視円錐が画面に収まる位置を探す
60度の視円錐を構成するための数式を探す
60度の場合は、だいたい710*710くらいだった。
したがって、1200/710=1.69..となる。1.7と繰り上げておく。
・正方形のキャンバスに限り、60度DP=HもしくはW×1.7となる。
イメージ図がこちら
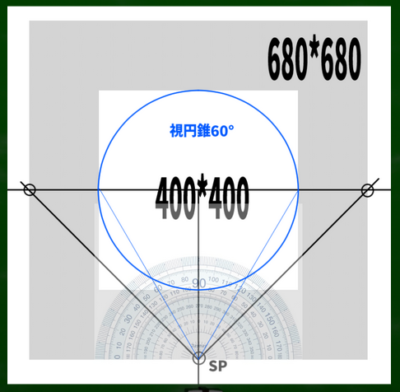
60度DP=HもしくはW×1.7で、Hを400とする。計算すると、およそ680になる。
この位置にDPを設定していく。おおよそ正しい位置にきた。つまり60度視円錐が画面にくる位置にきた(左右に60度)。
長方形の画面の場合の計算式を探す
前回の復習
【第三回】パースの基礎を学ぶ:一点透視図法で立方体を作成する方法、対角線の消失点について
さて、問題は「長方形」においてもこの数式が通用するかどうかだ。以前求めた計算式がこちらである。
- もし高さのほうが幅よりも数値が高い場合は、DP=2W+(H−W)となる。
- もし幅のほうが高さよりも数値が高い場合は、DP=2H+(W−H)である。
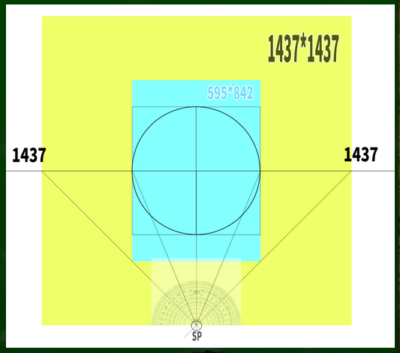
分度器を用いて引いていくと、意外な結果としてほとんど45度になるような視円錐の位置にきている。1437/595=2.41であることからも、2.4倍の計算式に近似する。以前、この計算結果を知って誤解したのかもしれない。
なぜそうなるのかは、ここでは考えないでおく。高さと幅の比率など、さまざまな要素が関係しているのかもしれない。ただし、この長方形における視円錐というのはやっかいな要素が潜んでいる。簡潔に言えば、「視円錐は楕円なのか」という問題である。
視円錐の性質上、正方形に納まるのではないか
そもそも視円錐の性質上、正方形に納まるのではないだろうか。
したがって、実際の視円錐はこのようになるのではないかと推測ができる。楕円の視円錐なるものが構成できれば別であるが、今回はそのようなケースを考えない。
45度の視円錐内により多く画面を収めたい場合の方法を考える
もし45度の視円錐内に全て収めたい場合は、もうすこし大きな視円錐を用いる必要があるのではないだろうか。
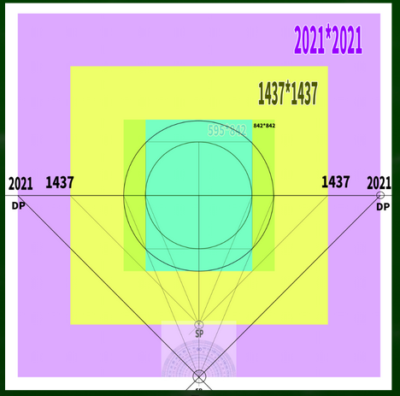
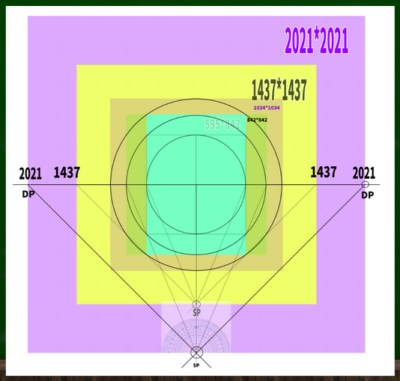
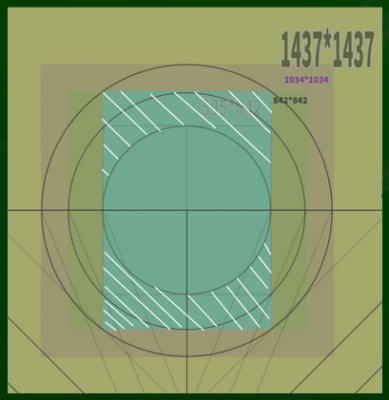
たとえば842*842のすべてが45度の視円錐に収まるようにするためにはどうすればいいのか。
・45度DP=HもしくはW×2.4となる。
それゆえに、842*842の場合はDPが2020.8の位置にくればいいということになる。2021としておこう。
図にするとこのようになる。
もちろん、完全にA4サイズを隅々まで埋めようとすれば、もうすこし大きな視円錐が必要になるのだろう。
この問題は、先程扱った正方形のキャンバスサイズにも言えることである。つまり、端のほうもすべて視円錐にどうしても45度でしっかり収めたいと考える場合は別の計算式が必要になる。絵を描く際にはほとんど気にならない歪みだと思うが、それでも気になる人がいるかもしれない。また、こうした歪みを気にして立点をどんどん下げる、つまり視円錐45度の円自体を大きくしていくと、全体に歪みとは違う違和感を感じる可能性も出てくる(遠くに感じるイメージ)。
45度の視円錐内に全て画面を収めたい場合の方法を考える
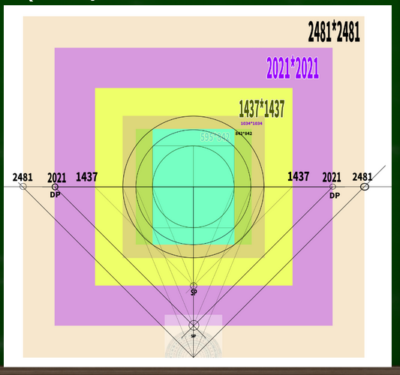
たとえば1034*1034の視円錐を考えると、すっぽり入る。この視円錐を45度にするためには、またさらに対角線の消失点を移動させる必要がある。
・45度DP=HもしくはW×2.4となる。
それゆえに、1034*2.4=2481.6の位置にDPがくるということになる。
部分の場合と全体の場合の計算式を探す
2つの選択肢
もしA4サイズ595(幅)*842(高さ)の画面を45度の視円錐におさめたい場合、選択肢が2つある。
- 画面を全て45度の視円錐に収めるケース
- 画面の一部分を45度の視円錐に収めるケース
1の選択をする場合、A4サイズをまるまる収めるような正円を考える必要がある。そして、その正円が納まるような正方形を想定する。
そしてその正方形から対角線の消失点の位置を把握すればいい。
全体の場合の数式
数式にすると以下のようになる。正円が収まるような一辺の長さをXとする。
X=√幅の二乗+高さの二乗
たとえばA4の場合は、X=√595*2+842*2となる。※「√(595^2+842^2)=」のようにグーグルで打ち込めばすぐ計算結果が返ってくる。計算結果は1031であった。さきほど目視で1034だと思っていたものが、正確には1031らしい。√はルートと読む。^2は2乗という意味である。今回は1034のまま利用する。
具体例:A4サイズの場合の「全部」のパターン
・45度DP=HもしくはW×2.4
次に、そのXに2.4をかければいい。X=1034だったので、1034*2.4=2481.6である。
2481*2481のキャンバスを作り、このキャンバスを基準にすればいい。
※2482に切り上げてもいい
あとは対角線の消失点を設定するだけで終わりである。
本来の描画画面に戻すとこのようになる。
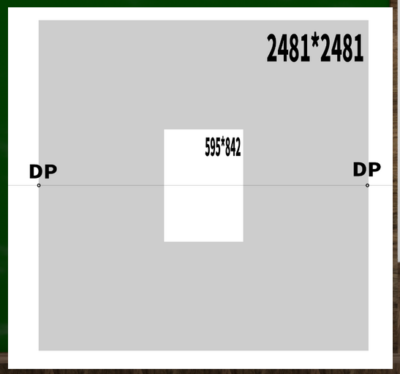
画面の一部分を45度の視円錐に収めるケース
では、最大幅の辺の正方形のみで収めるケースを考えてみよう。
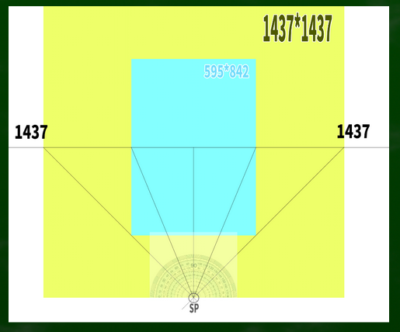
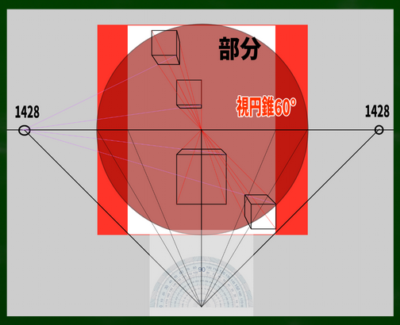
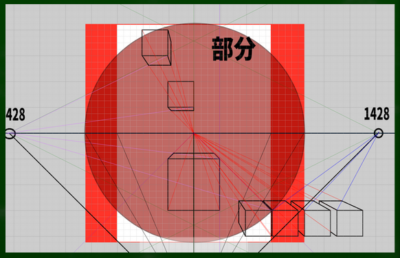
A4サイズ595(幅)*842(高さ)の場合は、595*595が視円錐45度に収まるのであり、それ以外ははみ出すケースである。
図でいうと、白い斜線の部分は視円錐45度の範囲外ということになる。
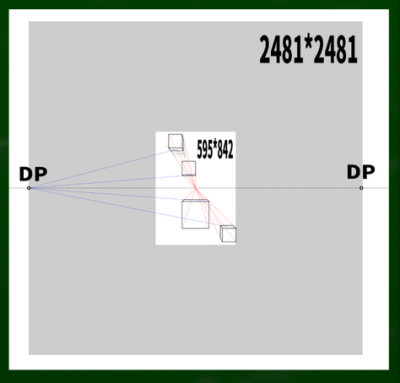
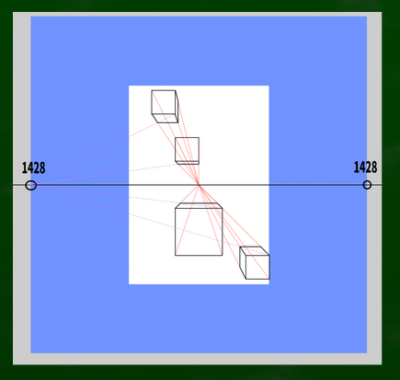
・45度DP=HもしくはW×2.4
式に当てはめると、595*2.4=1428である。この対角線の消失点を使って、立方体を先ほどと同じように描いてみた。
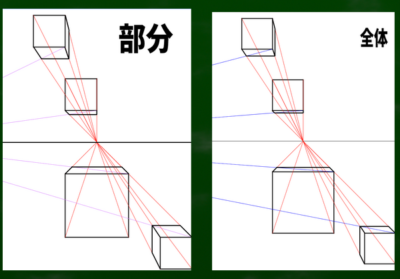
部分のケースと全体のケースで、立方体の歪みを比較する
たしかに比べてみると、画面全体をきちんと視円錐45度に収めたほうが綺麗な気もする。
特に、端の部分はすこし立方体が長く見える気もする。圧倒的な違和感というわけではないが、すこし気になる。全体の場合はすこし短い気もするが、このような感覚は実際の物体を見て感覚を鍛えるべきものなのだろう。これこそ芸術のセンスと関わってくる。
ちなみに、部分からはみ出てしまった範囲はどのくらいの視円錐なのだろうか。
この辺りが60度視円錐なので、大部分は60度視円錐内に収まっているといえる。この視円錐を超え始めると、60度を超え、歪みはもっと大きくなる。
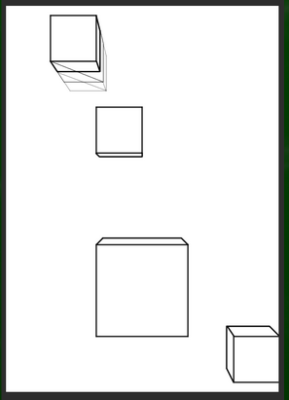
たとえばこの辺りに正方形を描くと、歪んで見えるだろう。
やはり一点透視図法の場合は部分よりは全部を45度視円錐、もしくは50度視円錐に入れたほうが安全なのかもしれない。二点、あるいは三点透視図法だと60度でもいいらしい。芸術に正解はないとはいえ、こんな隅に見せたい物を描くケースは稀だとも考えることが出来る。もし中心がより鮮やかに見えると仮定するならば、しかたない犠牲という考えもできる。
一点透視図法、二点透視図法、三点透視図法の各視円錐は何度にするべきなのか
スコット・ロバートソンによれば、以下の数値に収めれば自然な画面が得られるという。
一点透視図法の場合の適切な視円錐は何度にするべきか
視円錐は40度から50度以内に保つこと。視円錐を狭めすぎると、望遠レンズで撮影したようになってしまう。
二点透視図法の場合の適切な視円錐は何度にするべきか
視円錐は60度以内に保つこと。ただし、端の方は歪みが大きくなるため、重要な要素は端に描かないほうがいいらしい。
基本的に60度の視円錐で描かれることが多いそうだ。
三点透視図法の場合の適切な視円錐は何度にするべきか
視円錐は60度以内に保つこと。
※二点、三点透視図法の説明は別の記事で扱う予定
歪みを犠牲に得るものとはなにか
絵にどれだけのものを描き入れたいのか、どの程度の歪みならよしとするか
ロビー・リーは(DPの位置は)「絵にどれだけのものを描き入れたいのか、どの程度のゆがみならよしとするかで決まる」と述べている。
三分の二という数値を使って自然な画面を作成する
大抵の場合は「画面の端から消失点までを、画面の横幅の約三分の二の長さにするとうまくいく」ともリーはいう。
たとえば400*400の場合は、DP=400+(400*2/3)*2のキャンパスサイズの端だということになる。およそ933になる。
実際に作成してみたところ、およそ45度の視円錐が作成されている。
このあたりはもっと厳密な作図を行えば正しい値が得られそうだが、およそ44~46度の範囲といっていい。この計算結果は、45度DP=HもしくはW×2.4とも近似する。この場合は960となり、933と27の差がある。
さて、A4サイズの場合にもこの方法が利用できるだろうか。595*842で、幅を595とする場合を計算してみよう。
DP=W+(W*2/3)*2であることから、およそ1388.3となる。
実際に図示してみると、44~46度の範囲にきそうだ。つまり、おおよそ45度の視円錐におさまっているといえる。
しかし、これはA4サイズの「部分」ケースである。端の方は45度を超えてしまうというわけである。
もっとも、だからといってただちに不自然な絵になるわけではない。端の方でも60度以内におおよそは収まっているといえるのであれば、端であっても異常なほどの不自然な画面にはならない。
リーが述べたように、「どの程度のゆがみならよしとするか」を重視するべきなのだろう。
単なる歪みだけの問題なのか、歪みと視野の関係の問題を考える
そもそも、もし単なる歪みだけの問題ならば、我々があえて広い視円錐をとる必要性はないのではないだろうか。
45度視円錐、もしくは50度視円錐にすべての画面が納まるようなDPを設置するほうがいいという結論になる。たとえばX=√幅の二乗+高さの二乗で正円を計算すればいい。しかし残念ながら、視円錐の設定問題は、歪みだけの問題ではない。歪みを直そうとしすぎると、他の点が美的に、あるいは実用的にマイナスに作用する可能性が出てくる。
A4サイズの場合は、計算すると1031のキャンパスサイズを基準にすればいいということになる。
もしロビー・リーの計算法を使うならば、DP=W+(W*2/3)*2であることから、2405の位置にDPを設置すればいい。2.4倍を用いるなら、2474である。
視円錐の問題は「歪みと視野の関係の問題」だと言える。歪みを抑えようとして視野を小さくすれば、我々の視界もまた小さくなる。
もし目の前に物体が10個あったとして、45度の視円錐では5個しか描けず、60度の視円錐ではもっと描けるということがありうる。また、単にSP(立点)を離す方法、つまり目の前の物体から遠ざかって物を描く場合、たしかにより大きな範囲を描くことが出来るが、その分、細かく見ることはできなくなるのだろう。
絵を描く際の適切な視円錐の範囲、および立点の位置という問題は想像以上にやっかいであり、これといった絶対的な正解はないといえる。
明らかに歪むケースはよくない、という消極的なことしかいえないのだろう。もちろん、わざと歪ませたい場合は別である。
自然な範囲で、どれほどの歪みを許すのか、どれほどの絵のラフさを許すのか、どれほどの物を描き入れたいかなど、さまざまなクリエイターのセンスが試される。経験と知識の織りなす領域といえる。偉そうにこれが正解だ、などとは言えない。
大事なのは、クリエイターが作りたいと思った画面構成を手助けすることだろう。
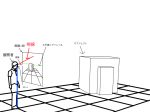
たとえばあなたがカメラマンだとして、目の前の生徒全員をファインダーに収めたいとする
もしファインダーに収まらない場合はズームアウトしたり、遠すぎる場合はズームインするのだろう。そもそも近すぎる場合はカメラマン自身が足を使って後ろに移動したり、遠すぎる場合は前に移動する必要がある。このように、距離と視野を調整するのである。
たとえば生徒が三人だけなら、この画面でも構わないだろう。
しかし、どうやらもっと生徒がいそうである。カメラのズームアウトで対処してみる。
ズームアウトというのは、要するに視野を広くするということであり、視円錐を大きくするということである。
11人全員(立方体)をファインダーに収めるために、視野角は約40度から104度にまで変更する必要があった。当然、端の方は歪んでしまうだろう。
そんなに歪んでいない、と思ったかもしれない。これは立方体同士が重なっているために歪みが和らいでいるだけである。
距離を開けてみると歪みはハッキリする。
さて、視円錐を広げないで、10人全員を収めるためには、立点を移動させるしかない。
つまり、カメラマン自身が後ろに下がる必要がある。y軸上に50mほど下がってみた。
あるいは生徒の縮尺を物理的に小さくする、ということもできなくはないが現実には難しい。
あるいは並び方を変える、(階段状の舞台を作って)寄せ集めて、できるだけ歪みを和らげた画角にするなども現実では可能であろう。後ろへ下がったり、視野を広げたりせずに画面に収める工夫も選択肢にはある。
カメラマン自身が後ろに下がった結果、得られた画面はこちらである。右側の歪みがなくなっている。
ただし、オブジェクトが小さくなっており、生徒の細かい顔の表情はおそらくよくみえないだろう。SP(立点)を下げるのとSPはそのままで視野を広くすることは歪みがあるかどうかの違いであり、どちらも全体的に鈍く、遠く見える。
両方とも視円錐40度だが、SPの位置が左のほうが近く、右のほうが遠い。制作における画面の大きさが指定されている場合は悩む必要がある。右の画像を、左の立方体と同じくらいの大きさに綺麗に拡大するという手もある(そんな大きな画像を並べられないので、一部を並べた)。
ドローイングの問題というより、構図の問題
我々は主にこの四択を強いられている。
- 大きく、鮮やかに部分を収める(自然な画面)
- 小さく、鈍く全体を収める(自然な画面)
- 小さく、鈍く全体を収める(不自然な画面)
- 大きく、鮮やかに全体を収めるように画面構成を工夫する
こうした問題はドローイングの問題というより、構図の問題と関わっていく。適切な画面構成、構図とはなにか、という芸術の根幹的な問題と関わり合っている。
大きく、鮮やかに全体を収める方法は難しい。小さく、鈍く全体を収めた画面を拡大するというような方法もなくはないだろうが、私にはまだ上手く画面に収めるイメージができない。たしかに同じくらいの大きさで見えるかもしれない。しかし、絵が大きすぎる場合、我々は一挙に、適切に、美的にそれらを捉えることは難しいケースが出てくるだろう。美はバランスの問題と大きく関係してくる。
カメラを撮る際には大きな制限がある(例えば富士山は動かせない)。
しかし絵で自由にオブジェクトを創り出す人にとっては、無理に画面を広げるのではなく、適切な画面にどれだけのオブジェクトを配置するべきか考える自由と悩みがあるといえる。すでに描いた絵を小手先でズームインやアウトをするのではなく、そもそも設計図(ラフ画)の段階で考慮するべき問題というわけである。
参考文献
初心者でもわかりやすい本
ロビー・リー「超入門 マンガと図解でわかる! パース教室」
・パース全般の基礎において一冊目にこれを手に取るのに適している。 ・私は「パース!マンガでわかる遠近法」よりも平易に、かつ丁寧に説明されていると感じた。それゆえに、初心者は特に一冊目にこの本をおすすめする。
デヴィッド・チェルシー「パース!マンガでわかる遠近法
・イラストが多く、わかりやすい。パースの基礎用語の説明もされていて、かつ平易にパースの使い方が説明されている良本。ただし、建築パースに特化しているわけではなく、「イラストレーション(漫画)」に特化している点を注意する必要がある。 ・パース全般の基礎を学ぶという目的において一冊目にこれを手に取るのに適している。
上級者向け
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
絵を描く、特に線画に特化した本。小難しいが広く、深く説明されている良本。
山城義彦「現代パースの基本と実際」
・パースの歴史や細かい用語が説明されていて便利。ただしメインはイラストレーションではなく「建築パース」に特化している点を注意する必要がある。 ・かなり小難しく説明されている(建築パースゆえにそうならざるをえないのだろう)。例えるなら文系が理系の数学を見たときのあの感覚に近い。建築家ならば通らなければならない道ではある。ただし、この本はだいぶ古く、現代ではコンピューターグラフィックスをもっと多用して楽をするのだと感じた。ただし、楽をするにもその原理を知っておいて損はない。
その他(パースがメインではない本)
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
・全般的な絵の知識が語られている本であり、パースに割かれる箇所は少ない。ただし、それなりにそれぞれ濃く説明されている本である。 ・パースを学ぼうとしてとる本ではないが、絵の描き方を学ぼうとする場合は選択肢に入ってくる。ただし高いのが難点。
コメント
この記事へのトラックバックはありません。




















この記事へのコメントはありません。