目次
はじめに
動画での説明
・この記事の「概要・要約・要旨・まとめ」はyoutubeの動画の冒頭にありますのでぜひ参照してください。
よろしければサイト維持のためにチャンネル登録をよろしくお願いしますm(_ _)mモチベになっていますm(_ _)m
一点透視図法(M点法)で立方体を描く
画面(PP)とは
画面とはなにか、意味、定義、わかりやすく解説
画面(Picture Plane,PP):視野を(たいていは)長方形に切り取ったもの。身の回りの三次元の世界にカメラを向けた時、ファインダーに映る二次元の画像のようなもの。
ファインダーとはなにか、意味、定義、わかりやすく解説
ファインダー:撮影範囲や焦点を調節するために、カメラに取り付けられたのぞき窓。
キャンバスとはなにか、意味、定義、わかりやすく解説
キャンバス(カンバス):主に油絵をかくための布。
油絵を描く場合の画面とは、この場合、キャンバスを意味する。
たとえばデジタルペイントでは、このような白い長方形が主にキャンバスと呼ばれている。
もちろん、長方形と決まっているわけではないが、代表的な形である。正方形でも楕円でも、星形でもかまわない。
大きな画面から特定の画面へ
私たちが「ある景色」を画面に収めようとする場合を想定してみよう。この場合、画面以外の景色も我々に見えている場合がある。
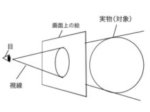
つまり、我々は「大きな画面(視野)」から「特定の画面(フィルター、キャンバス)」を切り取って、カメラを撮ったり絵を描いたりするということになる。
図にするとこのようなイメージとなる。
視野角
視野角とはなにか、意味、定義、わかりやすく解説
視野:視力の及ぶ範囲のこと。
視野角:目やカメラが一度に見ることができる範囲を角度で表したもの。
大きな画面、つまり視野がどのくらいかは動物によって、あるいは状況によって違う。
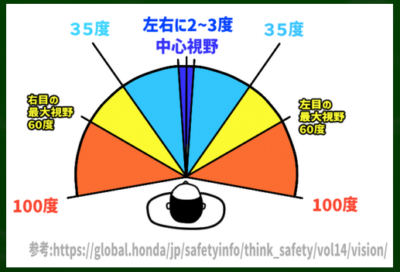
人間の視野角は水平に200度、垂直に125度くらい。
文字をしっかり認識できる範囲を「中心視野」といい、わずか1度から2度です。対象が歪まずに見える「有効視野」は左右に35度であるという。左右に約35度を超えるあたりから、視覚の解像度が低下し始め、「ぼんやり」とした感じになるというわけだ。
画角と立点の関係
立点とはなにか、意味、定義、わかりやすく解説
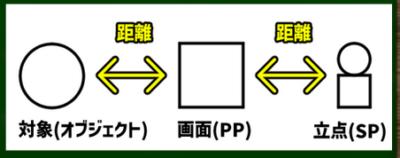
私たちがカメラを撮る時、または絵を描く時、我々の身体とファインダー(キャンバス)の距離は離れていることが多い。
対象物とキャンバスの間に距離があるように、キャンバスと我々の間にも距離がある。
キャンバスと目が密着するような距離で絵を描く人はまずいないし、それはカメラも同様だろう。距離があるという点が重要である。
画角:立点(SP)と画面(PP≒GL)の両端を結んだときにできる角度。視野角ともいう。
立点(station point,SP):観察者が描く対象を観察する定点のこと。カメラの位置ともいえる。
立点の位置次第で画角が変化する
重要なのは、画角と立点の関係である。端的に言うと、立点の位置次第で画角が変化するといえる。
したがって、絵を描く際にはまず「立点」を設定する必要性があることになる。対象とどのくらいの距離、位置関係を保つか、とも言い換えることができるだろう。
例えば対象に近づけば近づくほど(立点が対象に近づくほど)、多くの範囲が画面に収まらなくなり、遠ざかれば遠ざかるほど多くの範囲が納まるといえる。
カメラの場合はズームインやズームアウトでその距離を操作できるだろう。しかし人間の場合は、なんらかの道具を使わない限り、実際に足で前に進むか後ろに下がるかする必要がある。
不自然になってしまうレベルの画角について、いわゆるパース崩れとは
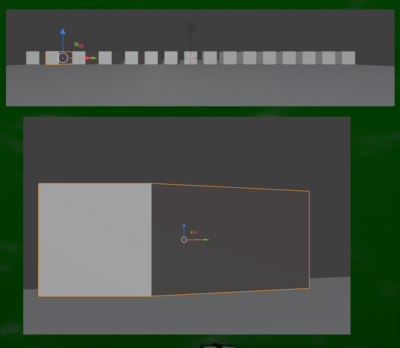
立点をイメージ化するとこのようになる。
近い場合の視野角は約18度で、遠い場合は約140度にしてみた。これは極端なケースである。
人間の自然な視野角は広くても60度であることを我々は先ほど学んだ。
視野角140度というのは本来ならば見えすらしない範囲である。また、そのような視野角で絵を構成しようとすると、立方体は歪んでしまう。つまり、絵が不自然になってしまうのである。立方体にはとても見えなくなってしまっている。
追記(2025/05/08):どうやら立方体と正六面体を混同して、「正立方体と表記してしまっていたようだ。そもそも立方体を直方体ないし単なる立体として認識してしまっていたのかもしれない。正方形で構成される立体が立方体であることを修正しておく。
我々は視界に入ったものや想像したもの「全て」を描くわけではない
視野角100度は、いわば我々の「視野(視界)」である。しかし、我々は視野に入ったもの全てを描くわけではないだろう。
たとえば目の前に見える広い花畑から、一輪の花にフォーカスを当て、それだけをキャンバスに収めるということも可能である。
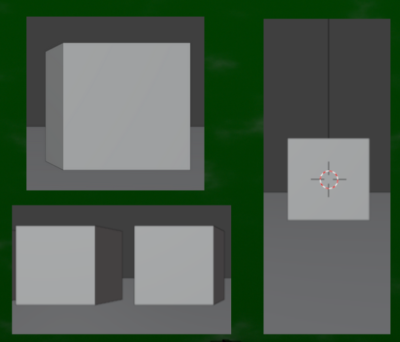
たとえば人間の最大の「視野」として100度(左右に)の景色がこちらである。
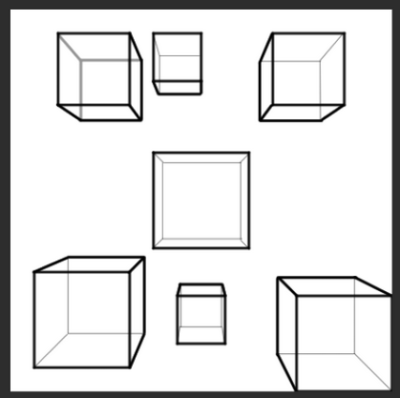
端のほうの立方体は歪んでしまっている。人間の視野は60度を超えたあたりから見えるには見えるが、しかし歪んで見えてしまうのである。100度を超えると、そもそも見えなくなるという話である。
われわれが絵を描く場合、たいていは中心視野に近いものを描くだろう。
斜め右にミケランジェロを置いてデッサンする人はいないだろう。たいていは真正面の、近すぎず遠すぎない位置に置く。われわれが自然だと思えるような位置関係にあるとき、たいていは自然な視野角で画面は構成されているのだろう。40度から60度くらいが自然だとよくいわれている。特に、目の前にオブジェクトがなく、想像で物を構成する場合はこの基準値が活躍することが多いだろう。
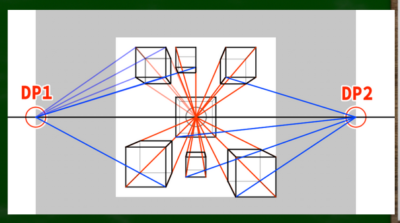
たとえば視野角100度の景色、つまり「大きな画面(視野)」から、ちょうど60度に納まるように「特定の画面(キャンバス)」を構成するとこのようになる。この特定の画面内の立方体はどれも大きくは歪んでいない、という点がポイントである。
もちろん、視野角60度の全ての景色を描く必要はない。この範囲において、どれを切り出しても、拡大してもいいわけである。場合によっては想像によって形を変えたり、違った配置を行うことも自由だ。
どの点にフォーカス(焦点)を当てるかがクリエイターの見せ所というわけである。
立点(SP)と基線(GL)の関係
基線、基面とはなにか、意味、定義、わかりやすく解説
立点(station point,SP):観察者が描く対象を観察する定点
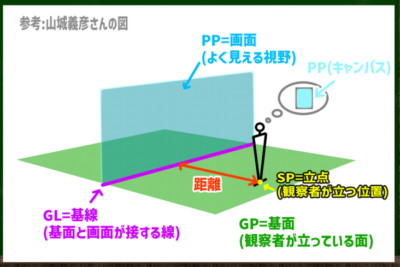
基線(Ground Line,GL):基面と画面が接する線のこと。
基面(Ground Plane,GP):対象物が置かれ、見る人が立っている面
我々が対象物を画面に写し取る時、殆どの場合、下には地面がある。部屋なら床であり、外なら小石や花畑、歩道かもしれない。この地面のことを「基面(GP)」という。
そして、この基面(GP)に人は立っていて、その位置を「立点(SP)」という。
この立点から対象物との間には距離がある。もちろん、対象物と「特定の画面」、たとえばキャンバス(紙など)の間にも距離がある。
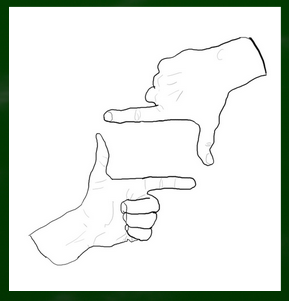
つまり、我々の視野(PP1)と、我々の視野から切り取った特定の視野ないしキャンバス(PP2)をわけて考えるということである。写実のイメージでいうならば大きな画面を切り取り、写し取るような感じである。もうすこし直感的なイメージを言うならば、両手で枠を使って狙いを定めて、それをキャンバスに写し取るようなイメージである。
その意味でいえばキャンバスと観察者との距離はあまり重要ではないかもしれない。
極論、まったく紙を見ないで絵を描ける人もいるので、キャンバスに対して人がどういう角度で見てるかはさほど重要ではない。大事なのはオブジェクトに対してどういう角度で見ているか、どういう角度でキャンバスにおさめたいかである。
図にするとこのようなイメージとなる。
対角線の消失点(DP)
対角線の消失点や測点とはなにか、意味、定義、わかりやすく解説
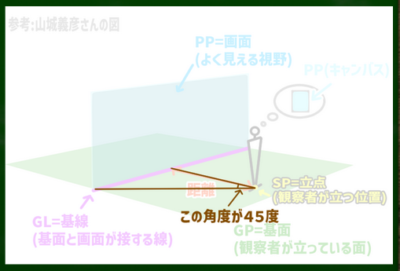
対角線の消失点(Distance Point,DP):立点からちょうど45度の直線を伸ばし、その線がちょうどアイレベル(IL)と交わる箇所の点のこと。測点(MP)の一種。
測点(Measuring Point,MP):水平線上に視中心から視点距離と同じ長さを測った距離点。平行透視の奥行きを図る場合に使う点のこと。測点(M)を利用した透視図法をM点法という。
「対角線の消失点」は消失点のひとつに数えていいのか
一点透視図法では、消失点が中央の一点だけしかないことが特徴である。それにもかかわらず、対角線の消失点なるものが存在すると、1点ではなくなるのではないか。
この疑問に関しては、MP(測点)やDP(対角線の消失点)は「あくまでも作画補助用の消失点」と考えればいいという点でなんとなく納得していくことにする。メインの消失点は1つだが、サブとして2つあるという考え方である。
参考:http://www.persfreaks.jp/main/1p/square/
対角線とはなにか、意味、定義、わかりやすく解説
対角線(Diagonal):多角形において、隣り合わない2つの頂点を結ぶ直線。長方形なら、向かい合うコーナーを結ぶ直線。
全ての多角形の対角線が45度というわけではないが、正方形の場合はつねに実測上は45度になる。
画角とは立点(SP)と画面(PP)の両端を結んだときにできる角度のことだった。
この角度が45度になるような位置に立っていればいいのである。こうした知識は実際に目の前にあるリアルなスケッチで気をつけるというより、目の前にないものを想像で1から構成する場合のテクニックに近い。
【具体例】400×400ピクセルのキャンバスにおける対角線の消失点はどこか?
たとえば400*400ピクセルの用紙があるとする。そして、この画面をちょうどキャンバスの画面にしたいとする。
この場合、どこに対角線の消失点は置かれるのだろうか。
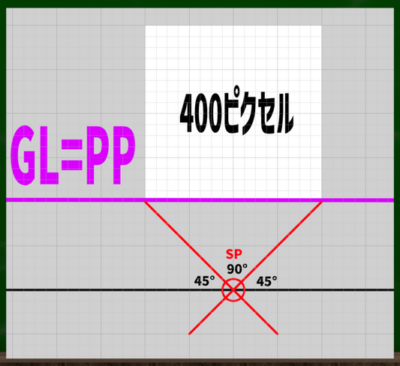
まずはSP(立点)がどこにあるのかを考えていこう。SPと画面(PP)は重ならないことから、SPは必ずこのキャンパスの外にあることになる。
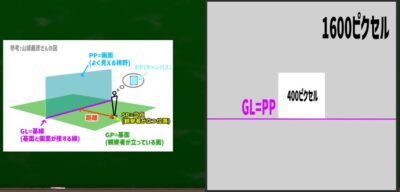
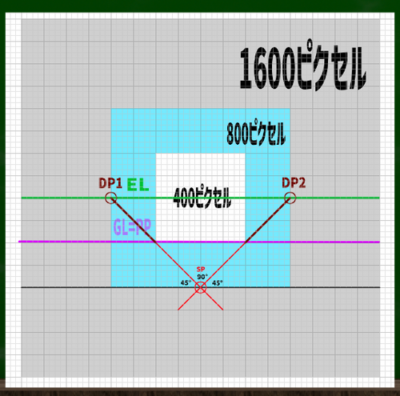
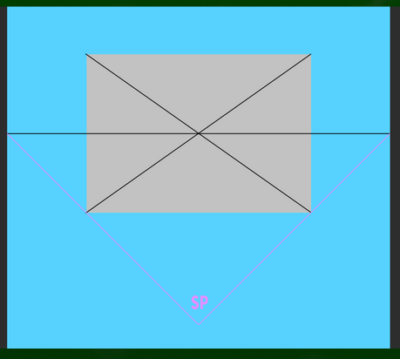
たとえば1600*1600ピクセルの内に400ピクセルのキャンバスを収めてみると、このようになる。
PP(画面)とGL(基線)が重なる線は、ここになる。
画面の端から、45度にまっすぐ線を引いた箇所が立点(SP)となる。
もちろん、どんなケースでもここに立点がくるというわけではない。画角が45度の場合はここにくるという話であり、60度や30度では違った位置に立点がくる。
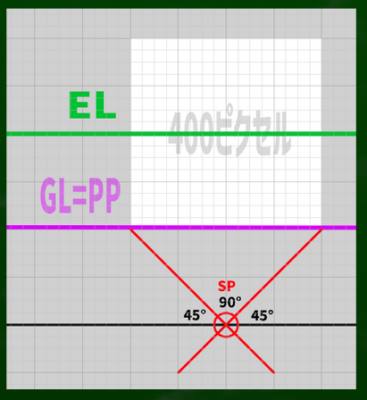
アイレベル(Eye level,EL):ある時点での視線(目)の高さを指す。アイレベルは、観察者の位置に応じて変化する。アイレベルはたいてい、実際の水平線(水面と空の境界)と一致する。
対角線の消失点(DP)は、さらにEL(アイレベル)と立点からの対角線が交わった箇所にある。一点透視図法において、アイレベルは基本的に画面の中央に位置する。
もちろん、絵によってはアイレベル(水平線)は上や下にくる場合もあるが、それは中央にきた画面を上や下の部分で切り取っているということである。背を伸ばしても、かがんでも、その視界内の中央にHLが来ることは変わらない。
我々は目で見たもの、あるいは想像したもの全てをキャンバスに取り入れるわけではなく、取捨選択を行う。
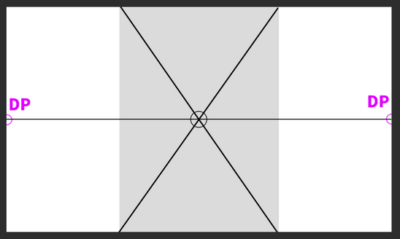
ELを画面(PP)の中央に引くと、このようになる。手書きで中央に引くことが難しければ、2つの対角線を使うといい。ちょうど対角線が交わる点に視心がくるので、その高さに水平線を引けばいい。
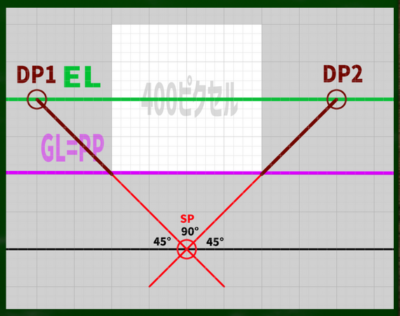
SPからELへ向かって真っ直ぐ線を伸ばしていくと、ELと交わる点が見つかる。ここが対角線の消失点(DP)である。
DPは基本的に画面の外にあるという点が重要である。
対角線の消失点をキャンパスサイズで調べる方法
正方形のキャンバスと長方形のキャンバスでは調べ方が違う?
先ほど面倒な作業をしていたが、あのケースに限っていば対角線の消失点は基本的に画面の横幅の倍のサイズを使えばいいという簡単な作業である。そもそも横幅も縦幅も同じサイズなので、単に2倍でよかった。
たとえば400*400ピクセルのキャンバスならば、800*800のピクセルの端の位置に対角線の消失点がくるということになる。
(800*800のキャンバスならば1600*1600の端になる)
A4サイズでDPIが72ならば、595*842ピクセルである。
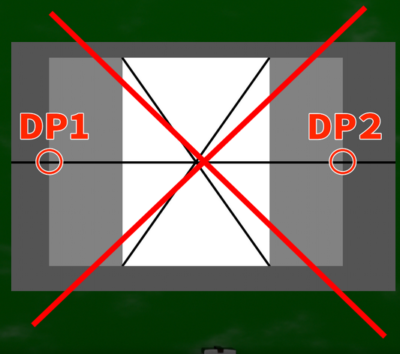
もし幅が595ピクセルならば、その倍のキャンパスサイズ、つまり1190ピクセルの位置に対角線の消失点(DP)がくるのだろうか。と、うまく行けばいいのだが、そうはうまくいかないようだ。
実際にA4サイズを用意し、画面の端からILへ線を伸ばしていくと、2倍のサイズと一致しないことがわかる。
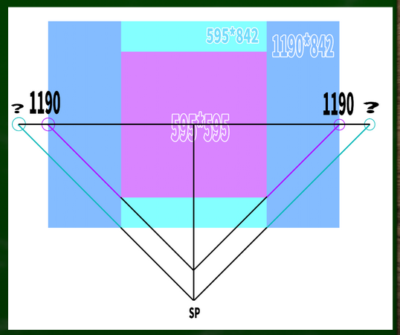
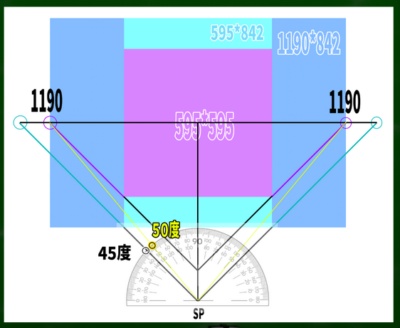
もしキャンバスが595*595のような正方形ならば、1190に対角線の消失点がくるのは適切だ。
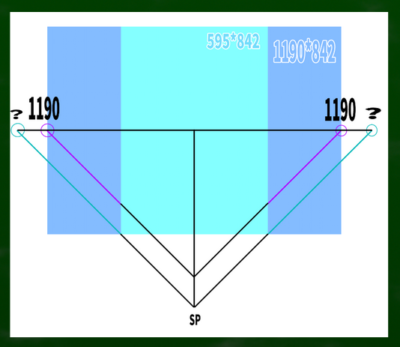
しかし、595*842のような長方形ならば、適切ではないということになる。
長方形のケースで、単に幅の2倍の位置に対角線の消失点をとっても歪まないケース?
ただし、1190の位置を仮に対角線の消失点としたとしても、595*842の画面は特段歪むわけではない。
いま焦点となっているのは、45度の対角線の消失点はどこかという話である。45度の対角線を使わないと歪むという話ではなく、40度から60度の範囲なら歪みにくいという話だ。もっとも、一点透視図法では40度から50度の範囲が推奨されることが多い。
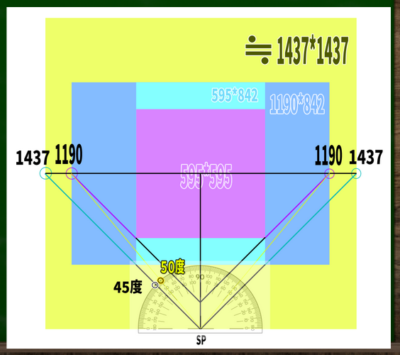
実際に画面の端、つまりGLから45度線に線を伸ばしていくと、1190よりも左側の、およそ1437ピクセルの位置に対角線の消失点が来る。
長方形の場合に対角線の消失点の位置を把握する方法を考えてみる
なぜ、1437ピクセルの位置にくるのか、その計算を推測してみた。まず、お互いの差を計算する。
新しくできた視心から対角線の消失点までの距離は、1437/2=718.5ピクセルである。
単に2倍してできた位置は1190なので、1190/2=595ピクセルである。したがって、718.5-595=123.5ピクセルとなる。
また、お互いの「高さ」の差分も計算する。
正方形の場合は幅と同じ595ピクセルだが、A4の場合は842ピクセルだった。
したがって、842-595=247ピクセルである。
差分が247と123.5であることがわかった。つまり、おおよそ1/2あたりの差異があるということになる。
したがって、A4サイズである595*842のキャンバスの対角線の消失点を近似的に知りたい時は、まず幅を2倍する。
そして、高さと幅の差分、つまり842-595=247を足せばいい。
つまり、DP=595*2+247=1437ということになる。視心から対角線の消失点までの距離の長さはこの半分の、718.5ピクセルである。
長方形の場合に対角線の消失点を出す数式
ややこしいので、簡潔にまとめよう
- もし高さのほうが幅よりも数値が高い場合は、DP=2W+(H−W)となる。
- もし幅のほうが高さよりも数値が高い場合は、DP=2H+(W−H)である。
【具体例】A4サイズ(595×842)の場合の対角線の消失点の位置
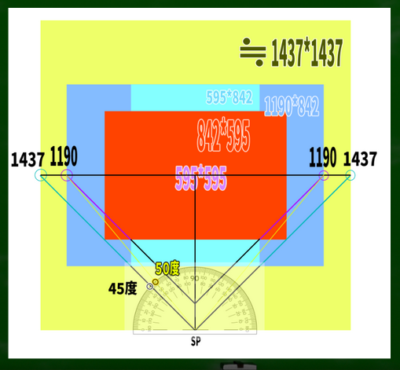
1:595(幅)*842(高さ)をつくる。わかりやすく灰色にぬっておいた。
2:幅を1437に変更する。アイレベル上の端が、対角線の消失点となる。
DP=2W+(H−W)
DP=2(595)+(842-595)
【具体例】B4サイズ(729×1032)の場合の対角線の消失点の位置
問題は、この計算が他の比率のキャンバスにも使えるかである。たとえばB4のキャンバスで実験してみよう。
B4は729(幅)*1032(高さ)である。したがって、差分は303である。幅の二倍である1458に303を足すと、1761となる。
図にすると、このようになる。
ここから、実際にGLから45度に線を伸ばして確かめてみる。
どうやら、おおよそ正しそうである。
【具体例】A4サイズ(842×595)の場合の対角線の消失点の位置
仮に、A4サイズの幅が842で、高さが595だった場合はどうだろうか。
DP=2H+(W−H)にあてはめていけばいい。DP=2(595)+(842-595)となり、1437である。実際にGLから45度の線を引いたところ、一致したことからも、おおよそ合っているといっていいのだろう。
高さが842だったときと同じDPに来るという点は興味深い。
高さと幅を入れ替えただけならば、同じDPが使えるということになる。
もちろん、デジタルソフトがなくてもこの方法は利用できる。正方形なら、A4用紙を3枚用意して、そのうち2枚を半分に折ればいい(あるいは2枚用意して、そのうち1枚を半分に切る)。半分に折ったA4用紙を、折っていないA4用紙の左右に並べれば対角線の消失点がわかる。
もちろん、正方形以外でも定規などを使って対角線の消失点を調べればできる。A4サイズなら一度作れば使い回しがきく。大きめの紙の中に絵を描いて、あとで切り取るという方法もありかもしれない。紐のような道具やパース定規を使う場合もある。
対角線の消失点を使って立方体をつくる
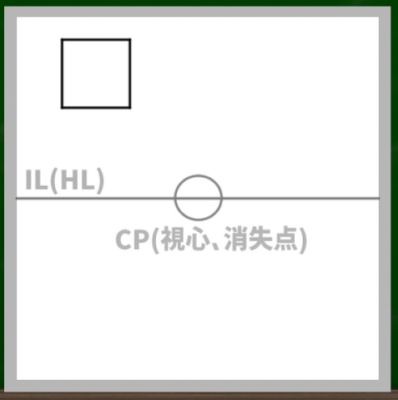
(1)まずは正方形を描く
では、さっそく立方体をつくっていこう。
たとえば任意の正方形を、このように適当に描いてみる。
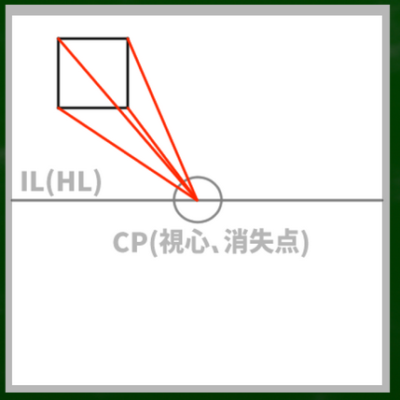
(2)視心と対角線の消失点に、各頂点を伸ばしていく
それぞれの頂点はただ1つの消失点へ向かって収束していくというのが一点透視図法の特徴であった。
つまり、このように収束していくことになる。しかし、どこまでの奥行きで区切ればいいのか、という点が(正)立方体作成の問題であった。
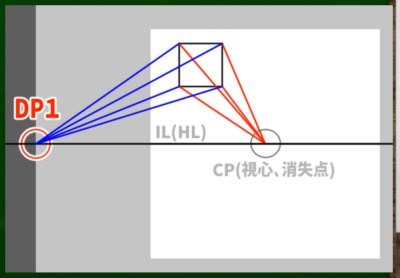
そこで、対角線の消失点を利用する。単に、頂点から対角線の消失点へ線を伸ばしていけばいいのである。右の頂点ならば左へ、左の頂点ならば右へ線を伸ばしていく。
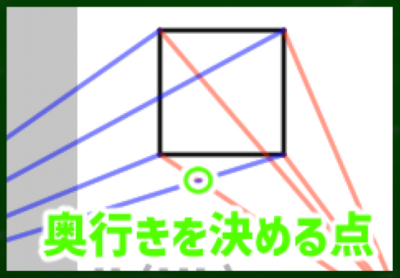
(3)「奥行きを決める点」を見つける
CP(VP,視心)へと伸びる線と、DP(対角線の消失点)へと伸びる線が交差する点が「奥行きを決める点」ということになる。
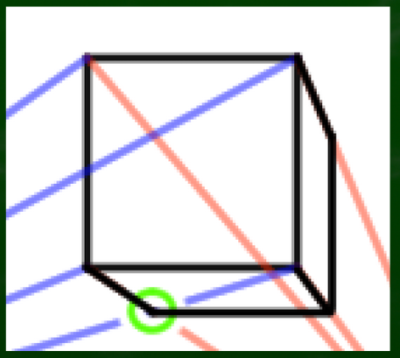
(4)「奥行きを決める点」を基準に線を伸ばしていく
あとは、この「奥行きを決める点」から線を伸ばしていけば立方体は完成する。
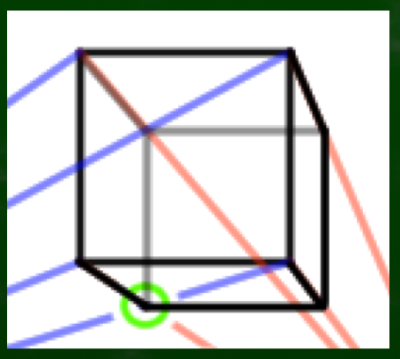
より精密に内部まで描けば、このようになる。
補助線を消すとこのようになる。
もちろん、どの位置に正方形を描いても、きれいに立方体ができる。
DPへの線は1本だけでも可能である。また、デジタルソフトを使えば、自動的にDPへ引けるように設定することもできる。
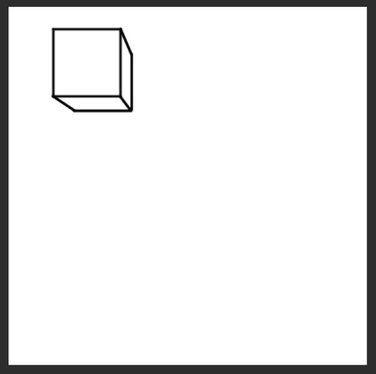
補助線を消して、キャンバスサイズを本来のサイズに戻すと、このように綺麗になる。
参考文献
初心者でもわかりやすい本
ロビー・リー「超入門 マンガと図解でわかる! パース教室」
・パース全般の基礎において一冊目にこれを手に取るのに適している。 ・私は「パース!マンガでわかる遠近法」よりも平易に、かつ丁寧に説明されていると感じた。それゆえに、初心者は特に一冊目にこの本をおすすめする。
デヴィッド・チェルシー「パース!マンガでわかる遠近法
・イラストが多く、わかりやすい。パースの基礎用語の説明もされていて、かつ平易にパースの使い方が説明されている良本。ただし、建築パースに特化しているわけではなく、「イラストレーション(漫画)」に特化している点を注意する必要がある。 ・パース全般の基礎を学ぶという目的において一冊目にこれを手に取るのに適している。
上級者向け
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
「スコット・ロバートソンのHow to Draw -オブジェクトに構造を与え、実現可能なモデルとして描く」
絵を描く、特に線画に特化した本。小難しいが広く、深く説明されている良本。
山城義彦「現代パースの基本と実際」
・パースの歴史や細かい用語が説明されていて便利。ただしメインはイラストレーションではなく「建築パース」に特化している点を注意する必要がある。 ・かなり小難しく説明されている(建築パースゆえにそうならざるをえないのだろう)。例えるなら文系が理系の数学を見たときのあの感覚に近い。建築家ならば通らなければならない道ではある。ただし、この本はだいぶ古く、現代ではコンピューターグラフィックスをもっと多用して楽をするのだと感じた。ただし、楽をするにもその原理を知っておいて損はない。
その他(パースがメインではない本)
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
「デジタルアーティストが知っておくべきアートの原則 改訂版 -色、光、構図、解剖学、遠近法、奥行き」
・全般的な絵の知識が語られている本であり、パースに割かれる箇所は少ない。ただし、それなりにそれぞれ濃く説明されている本である。 ・パースを学ぼうとしてとる本ではないが、絵の描き方を学ぼうとする場合は選択肢に入ってくる。ただし高いのが難点。
コメント
この記事へのトラックバックはありません。

























この記事へのコメントはありません。