【絵を描くための色彩学】ウェーバー・フェヒナーの法則とはなにか

フェヒナーの法則とはなにか
フェヒナーの法則の数学的理解
光の強さとフェヒナーの法則
ウェーバー・フェヒナーの法則という呼び方の是非について
- 個人的な数学の復習
参考文献

フェヒナーの法則とはなにか

フェヒナーの法則の定義

フェヒナーの法則(英:Fechnner’s law)：反応の大きさをR、刺激閾S0の倍数として表した刺激強度をSとしてR=K・logSとして表された関係をフェヒナーの法則、または対数法則(logarithmic)という。刺激強度が等比級数的に変化するとき、反応の大きさは等比級数的に変化することを意味する*1。

難しい定義はまず置いといて、簡単な話から理解しておきましょう。

フェヒナーの法則の具体例

たとえば「１００の刺激が１１０になったときはじめて『増加』したと気づくならば、２００の刺激が２１０に増加しても気づかず、気づかせるためには２２０にする必要がある」

という言い方をよくします。重さで考えてみましょう。１００ｇの重さから１０g増やすことではじめて重さの変化を感じたとします。これで「１0ｇ増やせば重くなるのか！」と思ってしまいますよね。しかし２００ｇから１０ｇ重くしても変化を感じません。２０ｇ重くしてやっと変化を感じるのです。

こういった経験はよくあるはずです。小さな音量からすこし音量を増やせば音量が大きくなったと変化を感じますが、大きな音量からすこし音量を増やしても大きくなったと感じません。10センチから1センチ長さをふやして長くなったと気づけても、1メートルに1センチを足しても長さを気づけません。もっと応用しようとすれば1万円の服が1000円引きなのと、100万円の服が1000円引きなのとではどちらがお得に感じるかといった身近な問題にまで広げることができるかもしれません。つまりフェヒナーの法則は五感全てにあてはめることができる法則だと言えます。ただし個人差や環境によってあてはまらないことがあるので注意です。目がいい人や重さに敏感なひともいますよね。

フェヒナーの法則と飽和

フェヒナーの法則では、「刺激が大きくなればなるほど刺激の変化を感じるために刺激量を大きく増やさなければいけないという法則」と解釈することもできます。つまり「刺激が強くなるほど、感覚の強さの増加度は小さくなる」ということです。鈍感になっていくとも理解することができます。お腹が空いているときはハンバーガを食べて幸せを感じると思います。ですが2個、3個、4個と食べるうちにどんどん幸せに感じる大きさは小さくなってくると思います。もうこれ以上食べても幸せほとんど変化しないよというのが飽和です。

フェヒナーの法則の数学的理解

フェヒナーの法則にウェーバー比を導入する

フェヒナ－の法則は「R=K・logS」でした。Rは反応の大きさを表し、Sは刺激強度を表します。

別の言い方をすれば「　E(感覚量<心理量>) ＝ｋ(定数)log R(刺激強度)」になるわけです。E=Rです。

ここでいうKは定数ですがウェーバー比を使います。

参考：種々のウェーバー比
重さ：1/40 ～1/30, 圧覚：1/7
音の大きさ：1/11,　明るさ：1/62
からさ：1/6.6,　あまさ：1/5,　酸っぱさ：1/4,　苦さ 1/4.8
ゴム臭：1/10
*4

このようにウェーバー比はさまざまあります。比率が大きければ大きいほど、鈍感になりやすくなります。感覚量(反応の大きさ)を増やすために必要な刺激量が比率が大きくなればなるほどたくさん必要だということです。

Kにウェーバー比あてはめるのですが、たとえばゴム臭の場合1/10でK=1.1となります。ウェーバー比が1/10ということは刺激量１０の変化には１増やさなければいけないということです。つまり１0を1.1倍する必要があります。ということでウェーバー比が1/10の場合、K=1.1になります。

これでE=1.1logRですね。

フェヒナ－の法則における刺激強度を理解する

「E(感覚量<心理量>) ＝ｋ(定数)log R(刺激強度)」のRが刺激強度になります。「R=K・logS」の場合はSが刺激強度になります。

刺激強度とは刺激量を基準となる最小刺激量で割ったものです。たとえば100gではじめて重さを感じた場合１００を最小刺激量とします。なにを最小刺激量とするかは感覚や表示によってかわります。

たとえば１００から１１０ｇに変化してはじめて重さを感じるとします。その場合の１１０ｇというのが刺激量にあたります。そして１１０-１００の１０ｇは最小刺激変化量となります。最小刺激変化量のことを弁別閾ともいいます。

弁別閾(べんべついき,difference thereshold difference ilmen)：刺激量が変化する場合に、その変化を知覚できる最小刺激変化量を弁別閾という。刺激量の方向は一般的に上昇、すなわち刺激量が増大してく場合と、下降、すなわち刺激量が減少していく場合の両方向が考えられるが、前者の場合の弁別閾を上弁別閾、後者の場合の弁別閾を下弁別閾といい、一般的に弁別閾というのはこの平均弁別閾のことを指す。弁別閾は差異が近くできることから丁度可知差異(just noticeable difference)または最小可知差異ともよばれる*1。

先程のウェーバー比と今回の刺激強度をあてはめることうなります。

「E(感覚量<心理量>) ＝1.1(定数)log 110/100(刺激強度)」

これで出る！と思ったのですがもうすこし手順を踏まないといけないみたいです。

指数関数の逆関数を使う（対数関数を使う）

さて　E(感覚量<心理量>) ＝ｋ(定数)log R(刺激強度)」とありますがまずは刺激量を求める計算式を出してみます。

【１】E(感覚量<心理量>) ＝ｋ(定数)log R(刺激強度)」

【２】刺激量＝100×1.1^（感覚量－１）

刺激量を求めるためには【２】の式を使う必要があります。感覚量と刺激量の関係は刺激量１，２，３と増えていくとしたら刺激量は1,1のx倍、1のx倍のx倍、1のx倍のx倍のx倍と増えていくことになります。つまり1,1.1,1.21,1.33と増えていくわけです。2を２でかけて、また２をかけてといった表現を乗数ともいいますよね。２の３乗を2^3といったように示します。このときの３を指数といいます。つまり【２】は指数関数といえます。

たとえば定数が0.1で最小刺激量が100のケースを考えてみます。

(例題)感覚単位が３の場合の刺激量を答えなさい

刺激量＝100*1.1^(3-1)＝121となります。

ちなみに感覚単位が2のときは100*1.1^(2-1)で110になります。

(例題)感覚単位２のとき、感覚単位を1増やすために必要な弁別閾を答えなさい

弁別閾とは変化を感じるために必要な刺激量でした。つまり感覚単位３の刺激量から感覚単位２の刺激量を引くことで求まります。

121-110で11です。つまり感覚単位２から感覚単位３にするためには１１の刺激が必要だということです。感覚単位１から感覚単位２にするためには１０の刺激量が必要だっあので、１の分だけ余計に刺激量が必要になっているということがわかります。このように感覚単位や刺激量が増えれば増えるほど弁別閾が増え、ウェーバー比が高ければ高いほど必要な弁別閾も増えるということがわかります。

【３】E＝log_1.1（R/100）＋1

この式は【２】の刺激量＝100×1.1^（感覚量－１）の指数関数の逆関数、つまり対数関数です。

S：x = a^pのとき、p = log_a x だから、
　　感覚量－１＝log_1.1（刺激量／100）
　　　　　　　　　（100は、本来は最小刺激量）
　　E＝log_1.1（R/100）＋1　･･･(3)

数学に疎い私は理解するのに苦労しました。【３】の右辺が＋１となっているのは感覚量ー１の－１を右辺に移行したからです。

S：x = a^pというのが【２】の刺激量＝100×1.1^（感覚量－１）にあたり、p = log_a xというのがE＝log_1.1（R/100）＋1にあたるということです。

実際に計算する

実際に計算するためには底の変換法則を利用する必要があります。「logab=logcb/logca」というものです。

E=log1.1*110/100になるわけですが、このままグーグル電卓に入れても間違った計算結果を叩き出してしまうので一度底の変換法則を適応させる必要があるということです。

つまり「log1.1*110/100」を「（log110/100）/log1.1）」に変換するということです。変換しないでもhttps://www.wolframalpha.com/input/?i=log1.1(1.1)のサイトでは計算結果が出るのでおすすめです。

（より数学的な理解をするとすれば、グーグルは常用対数の１０をとり、フェヒナーの法則の上記の例は自然対数のネイピア数をとるということです。 $Ln1.21/Ln(1.1) =log1.1(121/100)ということです。どちらもネイピア数で計算すれば2になりますが、グーグルの場合は常用対数１０で計算するので違う計算結果が出るということです。このへんはややこしいのであまり理解する必要はなく、単純にWOLFRAMで計算できるので計算内容は気にしないでください。グーグル電卓で「ln(1.21)/ln(1.1)=」と入力すれば２と計算結果が出ます。$ ）

さて表にしてみましょう。

今回はわかりやすくするために最小刺激量を１００とし、ウェーバー比を0.1とします。


刺激量	100	110	121	133.1	611.590904484	4114.47777893	186218.201326	1252782.93998	1378061.23398	17264116041.9
弁別閾	１０ (110-100)							125278.294 (1378061.23398-1252782.93998)
感覚単位	１	２	3	４	２０	４０	８０	１００	１０１	２００
計算方法			100×1.1^（3－１）=	100×1.1^（4－１）=	100×1.1^（20－１）=	100×1.1^（40－１）=	100×1.1^（80－１）=	100×1.1^（100－１）=	100×1.1^（101－１）	100×1.1^（200－１）=

結果はこのようになりました。感覚単位を１から２にするためには１０しか必要なかったのに、感覚単位を１００から１０１にするためには12万5278.294も必要になります。感覚単位が増える数は同じなのに、必要な刺激量な大きく異ることがわかります。これがフェフィナ－の法則です。刺激が大きくなればなるほど刺激に鈍感になるのです。


刺激量	100	235.7947691	1252782.93998
弁別閾	135.7947691	1252547.14521
感覚単位	１	10	100
計算方法	（235.7947691-100）	（1252782.93998-235.7947691）

感覚料を＋１から＋１０へとしたときは１０倍になりますよね。１０倍の感覚量のためには感覚単位１０の刺激量から感覚単位１の刺激量を引けばいいだけです。１から１０の感覚単位にするために必要な刺激量はおよそ１３５、１０から１００の感覚単位にするために必要な刺激量はおよそ125万2547です。全然違いますよね。

刺激量から感覚単位を計算することできます。

（例）１万の刺激量なら感覚単位はどれくらいか

wolframのサイトで「log_1.1（10000/100）＋1」と入力します。結果は「49.3177…」と出ました。感覚単位はおよそ49ということです。

この「49.3177…」を刺激量の式に入れてみると「100×1.1^（49.3177－１）」となり「9999.98488744」と出ます。つまりおよそ1万です。これで式の正しさが証明されました。

等比級数と等差級数

フェヒナーの法則は対数法則ともいわれ「刺激強度が等比級数的に変化するとき、反応の大きさが等差級数的に変化すること*1」ともいわれます。

等差数列：一定の数を足すことで次の項が得られる数列のこと

等比数列：一定の数をかけることで次の項が得られる数列のこと

等差数列と等比数列を理解することで上の文章が理解できると思います。たとえば１，２，３，４，５と並んでいる場合はそれぞれに１を足していけば次の項が得られます。１＋１＝２，２＋１＝３,３＋１＝４といったぐあいにです。こうしたものを等差数列といいます。等差級数的というのはこのような理解でだいたいOKだとも思います。

それに対して１，２，４，８，１６と増えていくような数列を等比数列といいます。1*2=2,2*2=4,3*2=6といったように一定の数をかけることで次の項が得られる数列を等比級数といいます。

フェヒナーの法則でいうところの等差級数における一定の数というのが「ウェーバー比」になります。

感覚単位は1,2(1+1),3(2+1),4(3+1),5(4+1)と増えていくので等差級数的といえます。刺激量は一定の数を1.1(ウェーバー比0.1)とした場合1,1.1(1*1.1), 1.21(1.1*1.1), 1.331(1.21*1.1),1.4641(1.331*1.1)と1.1を乗じていくので等比級数的だといえます。指数がつくので逆関数を使えるということで対数関係にあるというのだと思いますがそのへんの深い理解はまだできていません。

光の強さとフェヒナーの法則

明るさのウェーバー比0.01のケース

フェヒナーの法則は光の強さにも当てはまります。定数は諸説あります。経験的にいっても暗闇からすこし明るさを強くしてもすぐ明るさの変化を感じるように、最初のうちは敏感に変化を感じることができます。しかし光の明るさを強くしていくと、だんだん明るさを強くしても変化を感じにくくなります。これはウェーバーの法則と同様です。フェヒナーの法則は感覚単位に注目しただけで基本的にウェーバーの法則と変わりません。現在はスティーブンスのべき法則がより正確に感覚と刺激の関係を表していますが、ウェーバーやフェヒナーの法則でも十分理解できます。

参考：種々のウェーバー比
重さ：1/40 ～1/30, 圧覚：1/7
音の大きさ：1/11,　明るさ：1/62
からさ：1/6.6,　あまさ：1/5,　酸っぱさ：1/4,　苦さ 1/4.8
ゴム臭：1/10
*4

上のウェーバー比を見ると明るさに関するウェーバー比は1/62です。 0.016…ですね。

色彩用語辞典には「光るの明るさに関しては、観察者によって1/60から1/200に及ぶ*1」とあり、かなり幅があるようです。


刺激量	100	101	102.01	103.0301	104.060401	105.10100501	106.15201506	107.213535211	108.285670563	109.368527268
弁別閾	１	1.01	1.0201	1.030301	1.04060401	1.05101005	1.061520151	1.072135352	1.082856705
感覚単位	１	２	３	４	５	６	７	８	９	10
		101-100=	102.01-101=	103.0301- 102.01＝	以下略

外国のサイトには0.01とありました*4。いろいろ諸説はありますが0.01を採用したいと思います。最小刺激量は１００とします。ちなみに弁別閾は1.01乗でも求まります。たとえば感覚単位３の弁別閾1.01を1.01乗すると感覚単位4の弁別閾になります。感覚単位は1,2,3と増えていくのに弁別閾は1,1.01.1.0201と1.01を乗じた数でかけていくということになります。刺激値も同様です。ただし感覚単位１，２，３と続いている場合だけなので注意です。感覚単位１から１０の弁別閾を調べたい場合は刺激量Aー刺激量Bの引き算です。


刺激量	120.810895044	122.019003995	162.834833846	164.463182184	267.803349448	270.481382942	2054617.74707	2075163.92454
弁別閾	1.208108951		1.628348338		2.678033494		20546.17747
感覚単位	20	21	50	51	99	100	999	1000

光の場合はウェーバーが1.01なので、1単位あたり1%ずつしか増えていかないので人間は光の明るさに対してかなり敏感だといえます。わずかな量の変化でも変化したと気づくということです。たとえば感覚単位１から２にするために必要な変化量(弁別閾)は1.01でした。２から3にするために必要な弁別閾は1.0201です。しかし99から100にするためには2.67必要になってきます。緩やかですがだんだん変化したと感じるために必要な刺激量が大きくなってきています。重要なのは同じ感覚単位、１増やすということのために必要な刺激量が変わってくるということです。もっと数を大きくしていくと、999から1000にするために必要な刺激量はおよそ2万546です。このように刺激量を大きくすればするほど人間は鈍感になっていく、変化に気づきにくくなっていくということができます。鈍感になっていく早さが違うだけで、基本的に五感はほとんどの場合刺激が増えるほど鈍感になっていきます。

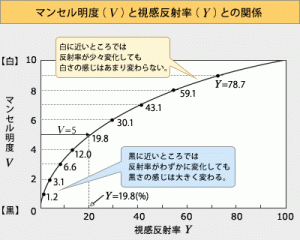
フェヒナーの法則と「明度と視感反射率」の関係について

*1

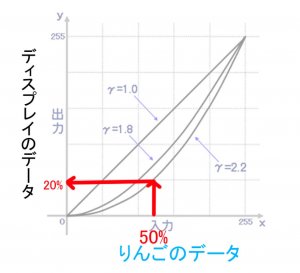
さて私がフェヒナーの法則を学んだのは視感反射率がわからなかったからです。上のグラフを見てください。もうみなさんも理解できると思います。この図はまさにフェヒナーの法則の、おそらくウェーバー比0.01を簡易的に1-100%でグラフにしたものです。

視感反射率が刺激強度だとしたら、マンセル明度は感覚単位に相当します。人間の五感の感覚量は大雑把には受ける刺激の強さと対数関係にあるのです。さてこの対数関係とはなにかというのを今回は学んできたわけです。別の言い方をすれば感覚量は等差的、刺激量は等比的に変化しているということです。この等比的というのは乗じていくことなのですが、それがウェーバー比によってなにを乗じるかが異なるということです。光の明るさ、つまりここでいう輝度(視感反射率)の場合はおそらくウェーバー比を0.01、すなわち1.01を乗じていくということです。

ウェーバー比が小さいので最初は緩やかです。グラフを見ると、わずかな視感反射率の変化で、マンセル明度は大きく変化しています。視感反射率が２０の時点でマンセル明度はおよそ５０%に達しているのです。これはすごく簡単に言えば光の強さ２０％で人間は５０％ほどの明るさに感じるということです。

*2

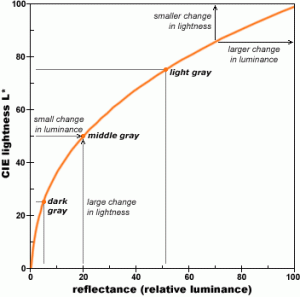
別のグラフを見てみましょう。外国のグラフです。刺激強度に相対的な輝度、感覚単位に明度をとったグラフです。基本的に先程のグラフと変わりませんが、ｙ軸が１-１００なのですこしわかりやすくなっていると思います。輝度２０％は明度５０％に相当するよというグラフです。

要するに明るくなるほど肉眼で感じる明度感は飽和してく、だんだん鈍感になっていくということです。

フェヒナーの法則とガンマ補正の関係について

ガンマ(gamma)：コンピュータの画像処理においては「中間調（グレー）の明るさ」を示す用語として使われるのが一般的*5

※写真におけるガンマは少し概念が異なる。「ガンマは写真感光材料のコントラストの程度を表す。ガンマが大きいものを硬調であるといい、微妙な明度差を表現できる*1。」

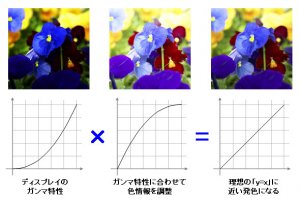
ガンマ特性：PC環境で「色」を扱うハードウェアには、ディスプレイ、プリンタ、スキャナなどがある。これらの機器をPCとつないで利用する際には、それぞれに色情報の「入力」と「出力」が発生するが、各機器には固有の発色特性（いわば、クセ）があり、入力された色情報をそのまま素直に出力できない。この入出力における発色特性のことを「ガンマ特性」という*5。

ガンマ補正：通常、ディスプレイのガンマ特性は中間調が暗くなる傾向にある。そこで、あらかじめ中間調を明るくしたデータ信号を入力し、「入力：出力」のバランスを「1：1」に近づけることで、色情報を正確にやり取りできるように工夫している。このように機器側のガンマ特性に合わせて、色情報を調整して帳尻を合わせる仕組みを「ガンマ補正」と呼ぶ*5。

*3

フェヒナーの法則を学んだ後は「ガンマ補正」が理解しやすくなっていますね。このガンマ補正はフェヒナーの法則をさらに正確にさせたスティーブンスのべき法則を参考に作られていますが、光に関してはそこまでグラフの違いがないのでフェヒナーの法則を理解していれば問題ありません。

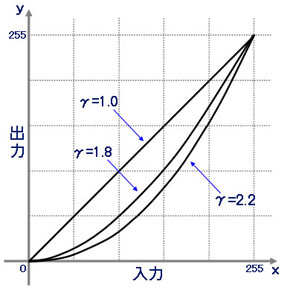
さて下の図の真ん中のグラフをみてください。どこかで見たことありませんか。そうです、光の明るさに関するグラフにそっくりです。X軸が増えれば増えるほど、Y軸は伸びにくくなっています。つまりX軸とY軸の関係は対数関係にあるのです。そしてこの対数関係にあるということは、人間の目の仕組みということです。

下の図の左側のグラフをみればディスプレイのガンマ補正をしなければいけない理由がわかります。ディスプレイのガンマ特性はフェヒナーの法則とはちがう向きになっていることがわかります。この人間にとって不自然なディスプレイのガンマ特性を補正する、調整するというのがガンマ補正なのです。

フェヒナーの法則では簡易化した光の明るさに関するグラフで刺激量２０で感覚単位５０に感じると習いました。たとえば自分が絵を描いたとします。R123、G０、Bのりんごの絵です。Rが123ということは輝度がおよそ50％ということです。この５０％というのは刺激量に値しています。そしてデータが輝度50%としているのだから、ディスプレイの最大の明るさの半分で表示したとします。人間はどれくらいの明るさを感じるのかという問題です。

ディスプレイが５０％の刺激をそのまま使用してしまえば、人間の感覚的には75%くらいに感じてしまうのです。りんごのデータはたしかに輝度50%ですがそのまま入力してしまうと人間は明るさを75％ほどに感じてしまうのです。この問題を補正するためには、データが５０％の輝度なら、ディスプレイの輝度の出力は２０％にすれば人間が明るさを50％に感じることができるのでうまくいくということです。これがガンマ補正なわけです。*3

上の図はY軸に出力、X軸に入力とあります。この出力がディスプレイの輝度だとすれば、入力はデータの輝度です。先程のりんごのデータが輝度５０％だとすれば、実際にディスプレイで出力される輝度は20%に調整されるということです。輝度20％でも人間の目には明るさとして50%程度に感じるので最終的にはデータの50%と一致するよということです。これがガンマ補正です。

一般的なガンマ補正は2.2というものが使われているみたいです。macなどは1.8が使われるものもあるみたいです。またsRGBはガンマ補正2.2に該当しているのもポイントです。

最近の液晶ディスプレイはディスプレイがきちんとガンマ補正をしてくれるので、あまり気にする必要はないように思えます。ただデータとして輝度５０％と入力したからといって、輝度がそのまま50%出力されていると思うのは間違いなので注意してください。人間の目を考慮して輝度は20%程度に抑えられています。

ウェーバー・フェヒナーの法則という呼び方の是非について

色彩用語辞典によれば「ウェーバーの法則は、感覚的な弁別ということが介在しているにせよ、物理的な測定値、ΔSとSとの関係を記述しているにすぎない。それに対して、フェヒナーの法則は、感覚的の増分がウェーバー比に比例して生じるという仮定から導き出されたにせよ、結果として反応と刺激との関係を記述する精神物理学的法則となっている。したがってウェーバーの法則とフェヒナーの法則は、別の法則であって、１つの法則であるかのような言い方がなされるのは適切ではない*1,63P」とありました。

フェヒナーの法則はウェーバー比を利用するのでウェーバー・フェヒナーの法則と呼んでも問題はなさそうですが、１つの法則であるかのような言い方は問題があるそうですね。個人的にはフェヒナーの法則と呼んだほうが短くていいと思います。