まえおき
よく丸に十字を描いて顔を描けだとか、顔全体に比率を覚えて顔を描けだとか言われます。個人的にイマイチしっくりきませんでした。
今回紹介する正三角形を使った顔の描き方は意外とよかったです。正三角形さえ綺麗にかければ顔がどんどん出来上がっていくのは面白いですね。
応用すれば十字も正三角形を利用してより正確に描けると思います。さらにパースを理解することによって三角形の見え方の変異を習得することができます。自由に顔が描けるようになります。
実際問題として絵に決まった比率などはありません。今回紹介する比率は成人の比率に近いです。子供と大人の比率は違いますし、男女でも違います。もちろん人によっても違います。自由に大きくしたり小さくしたりしてもいいのです。ですがそうした比率も基本的な比率からどの程度比率を変えてバランスを保つかにすぎません。左右ぐちゃぐちゃで歪んだ目はやはり不自然だと思います。
美術の世界では「ものの構成のパターン」を探求することが重要とされています。自分で研究してみましょう。算数や数学の知識があるとより創造性は広がるかと思います。自分が美しいと思う目の位置はaだから、それを元にして三角形を描いて・・など様々なパターン作りができます。
ルーミスさんは「熟練とは障害を克服することにほかならない、まず第一の障害は今始めようとしていることに対する知識の欠如がほとんどである」と言いました。まさにそのとおりだと思います。
絵を熟練させるためにはまず障害を克服しなければならない。そして障害を克服するためには問題(障害の原因)を見つけなければならない。いわゆる問題発見能力と問題解決能力です。
顔がうまく描けないという障害に対して、知識の欠如が原因であるという問題を発見します。そして必要な知識は比率であるという仮説を立て、情報収集を行い、分析を行い、問題を解決します。仮説が間違っていた場合はさらに情報収集して仮説をたて、実証するのです。この繰り返しが絵の熟練過程だと私は思います。
正三角形について
正三角形とはなにか
デジタル大辞泉によれば三角形とは「三つの線分で囲まれた多角形」です。
今回は3つの線分が等しい長さの三角形について主に扱います。いわゆる「正三角形」です。
正正三角形(せいさんかくけい、英: equilateral triangle)は、正多角形である三角形である。つまり、3本の辺の長さが全て等しい三角形である。3つの内角の大きさが全て等しい三角形と定義してもよい。1つの内角は 60°(π/3 rad)である。また一つの内角が60°である二等辺三角形は正三角形となる(wiki)。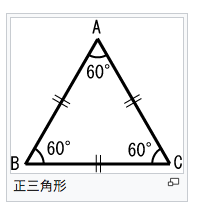
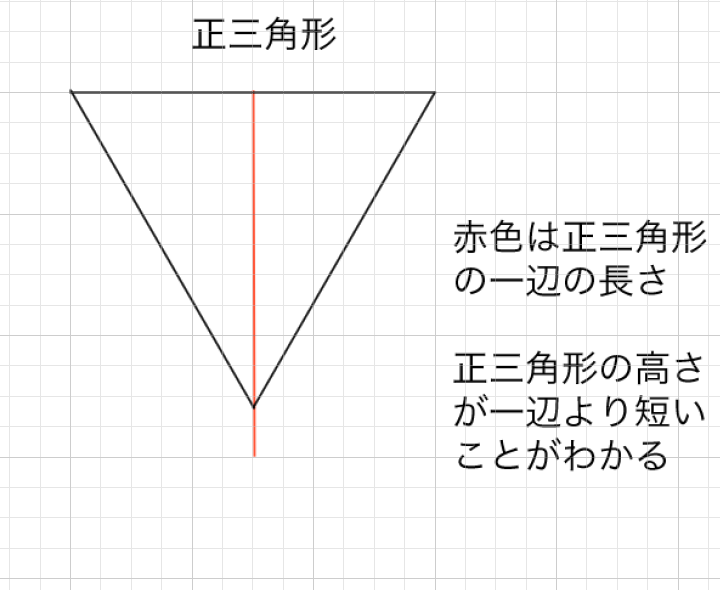
ちなみに正三角形の高さは一辺をaとするとa(√3/2)です。a=6センチだとします。6(√3/2)=3√3となります。√3は1.7くらいなので5.1となります。正三角形の一辺より高さは低いことがわかります。
升目などを使って三等分できる線を引いてみます。分度器で60度の位置に向かって最初に引いた線の中央に線を引いてみます。そうすると正三角形ができます。
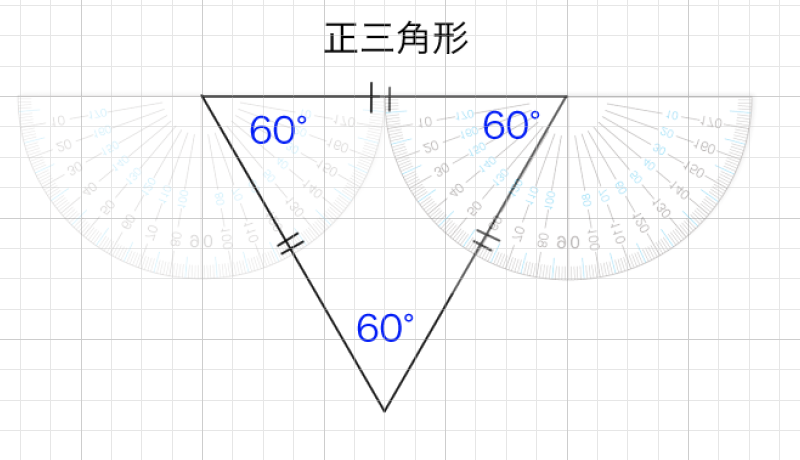
3等分した線を最初に引きました。これを3センチだとします。一辺の長さが3の正三角形の高さは3*√3/2です。約2.6センチほどの高さとなります。正確には2.59807621135..です。
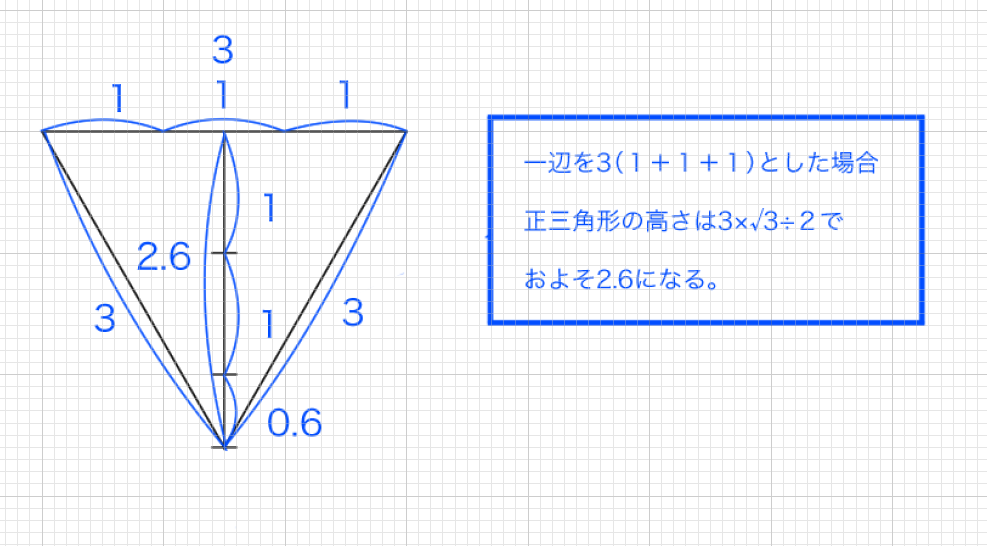
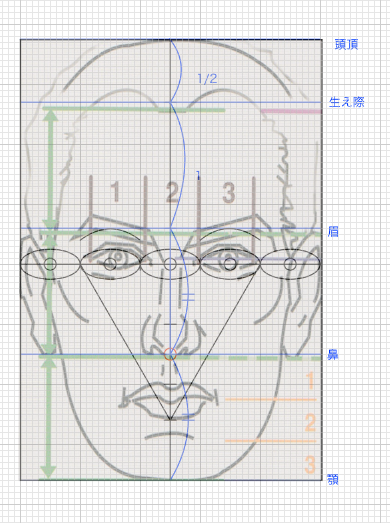
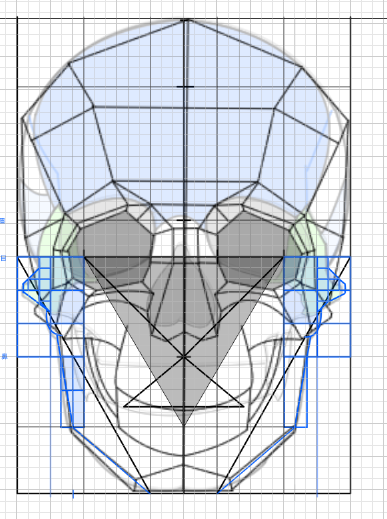
正三角形と顔の比率の関係について
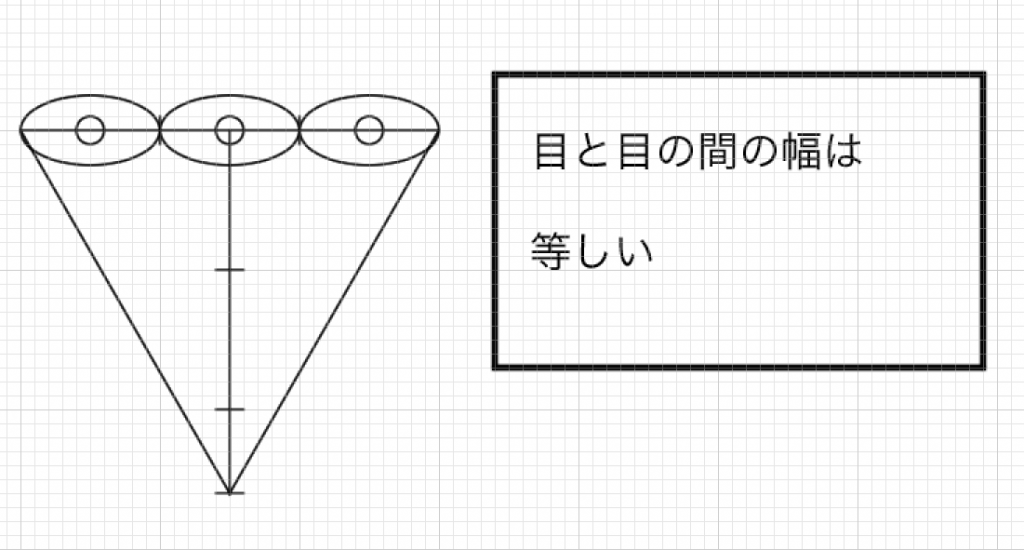
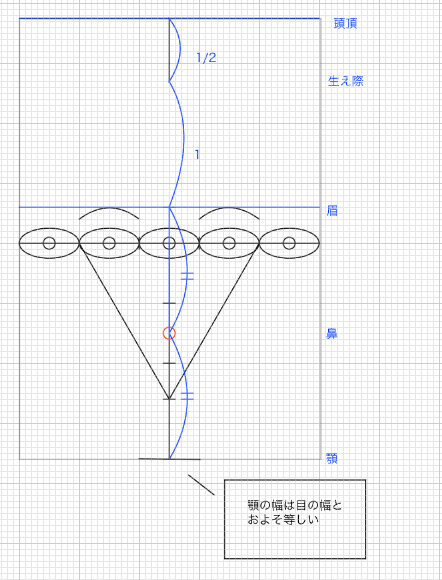
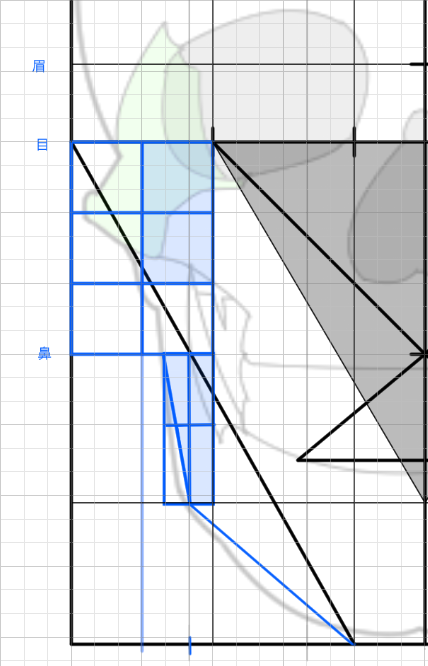
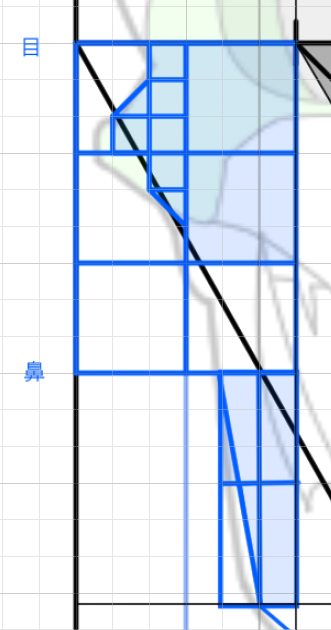
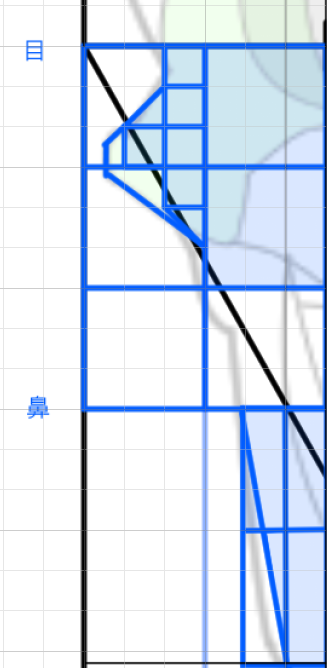
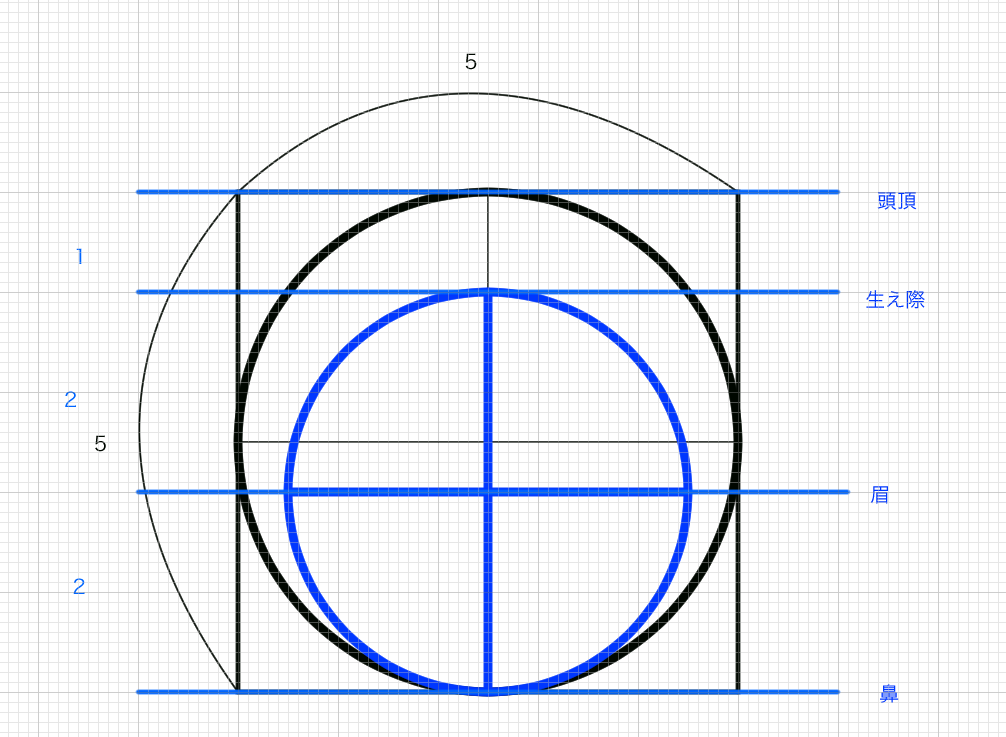
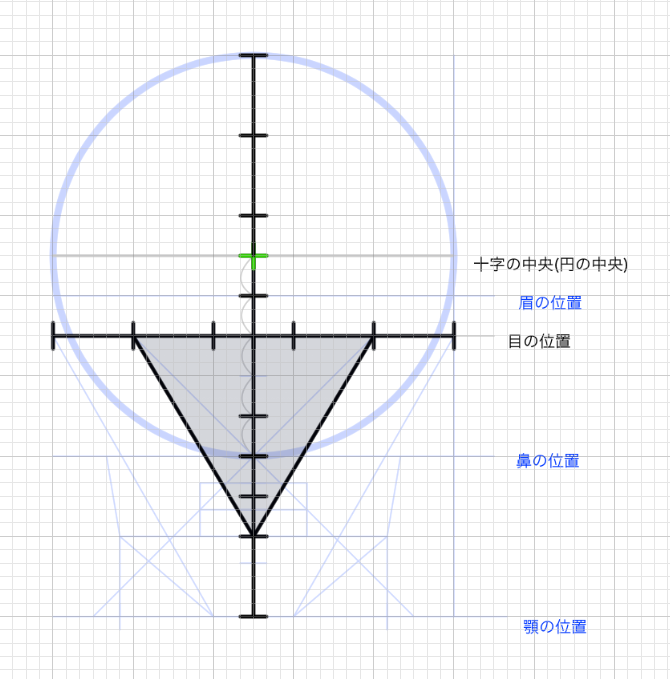
「目」と「両目の間の幅」は等しい
「目と目の間の幅は等しい。この法則をまず覚えます。正三角形の1ぺんを三等分にした場合、ちょうど目が三個入る横幅になります。目の大きさや位置は後ほど検討します。
顔の横幅は目が5つ分
顔の横幅は目の横幅5つ分です。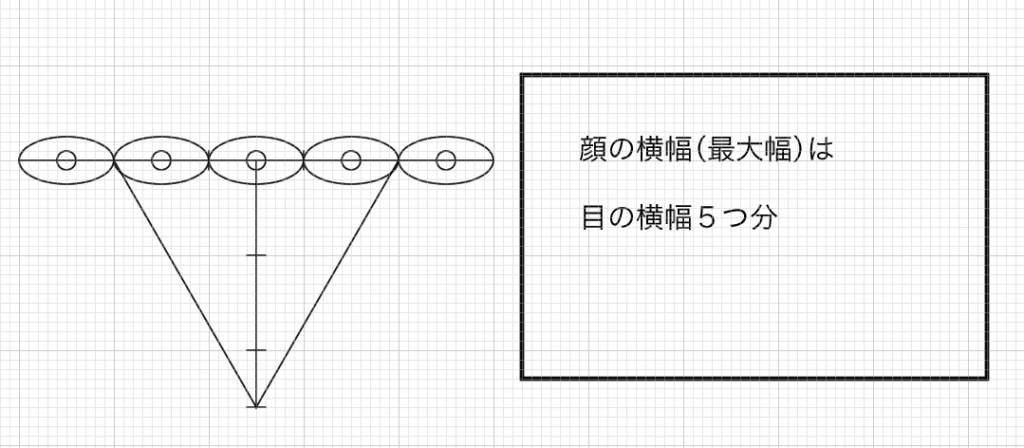
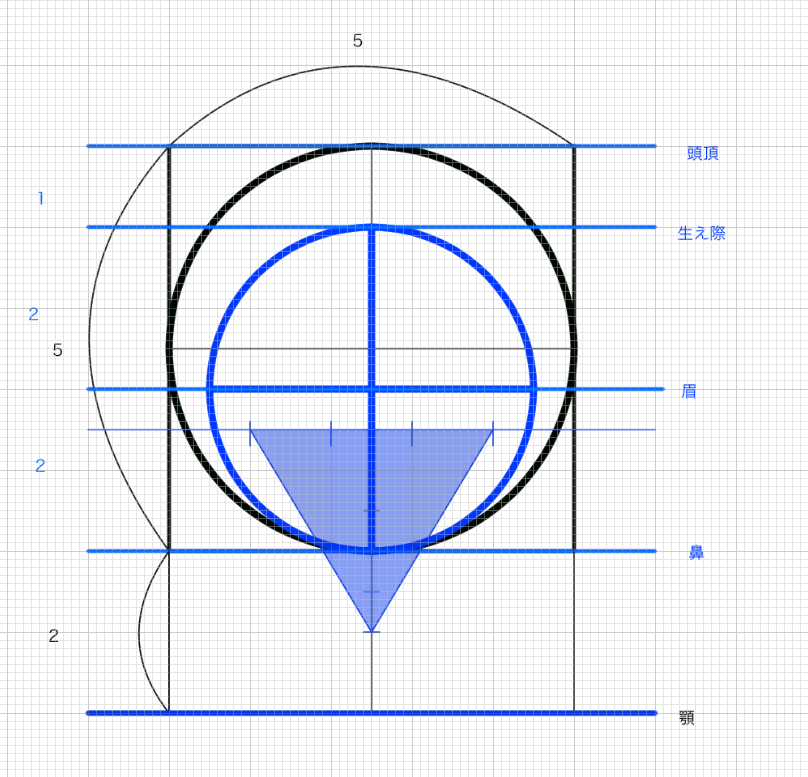
「口の下部」は「正三角形の高さの位置」、「顎」は「正三角形の高さ+1」
(あごの位置は正三角形の高さに1辺を足した位置にある)正三角形の高さに一辺の高さを足すと顔の最下部(あご)の位置になります。口の下部は正三角形の一番下の位置にあります。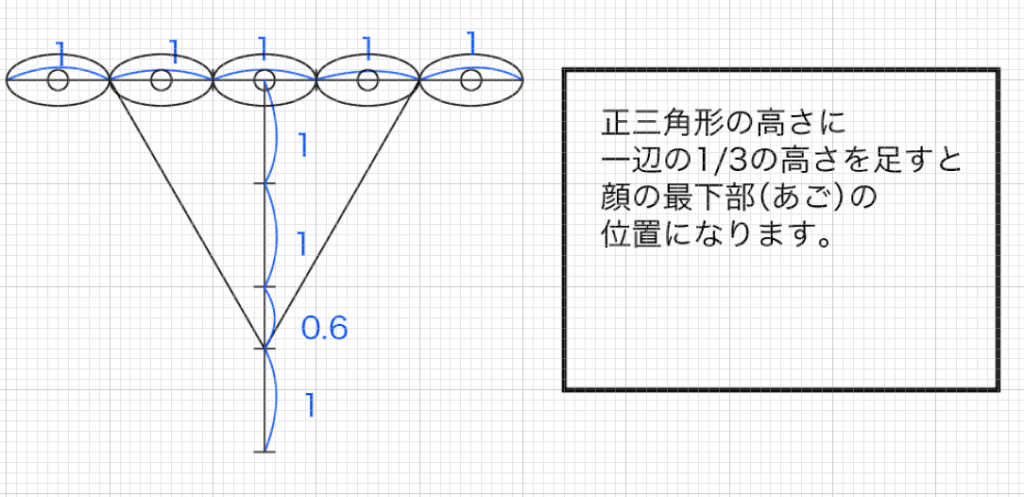
「目の高さ」は「目の幅の半分」
これはあくまでも基本です。個性的な目の場合はもっと高いかもしれませんし、大きいかもしれません。萌え絵などアニメ的な目などはもっと大きいです。
(目の高さは目の幅の半分)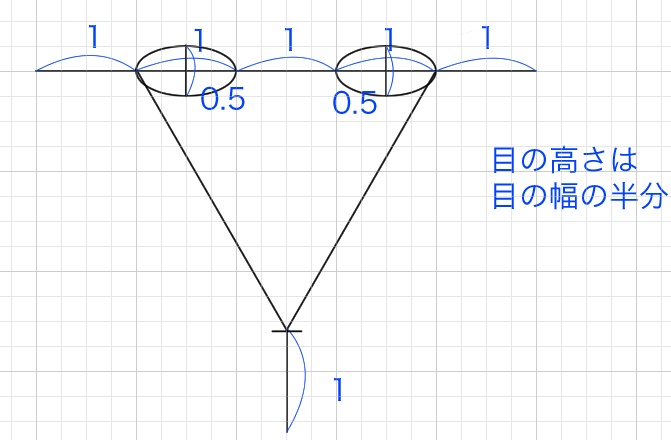
「眉の高さ」は「目の幅」
(眉の高さは目の高さの二倍の位置)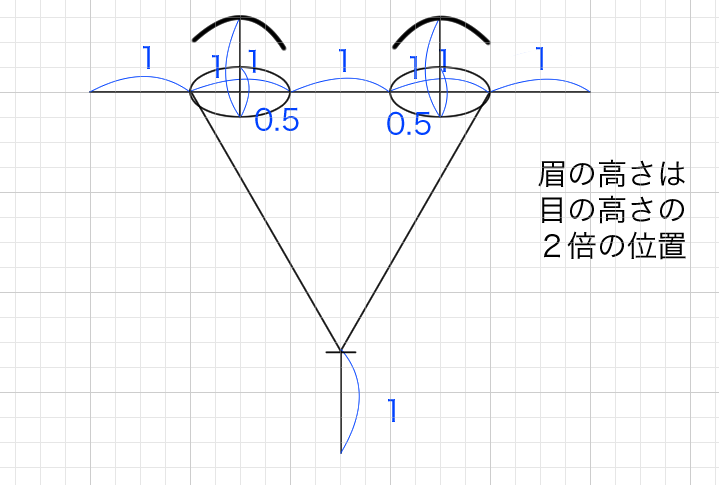
「鼻の高さ」は「目の端から45°に伸ばした位置にある」
(鼻の高さと目の幅の関係)鼻の高さは目の幅から45°に線を伸ばした位置にある。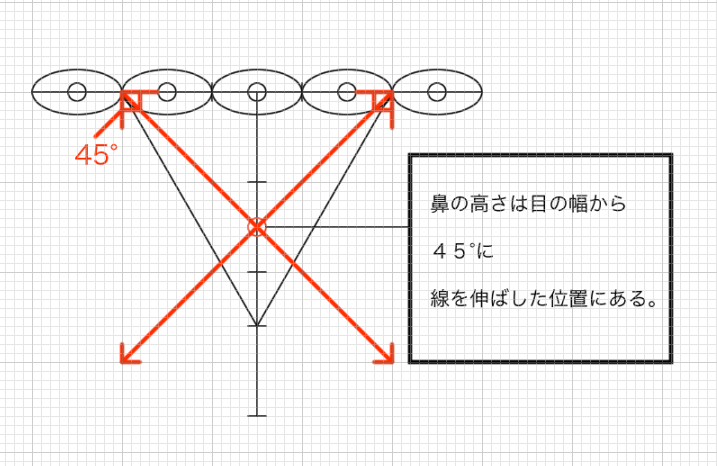
ちなみにこの線は口の横幅にも使えます。
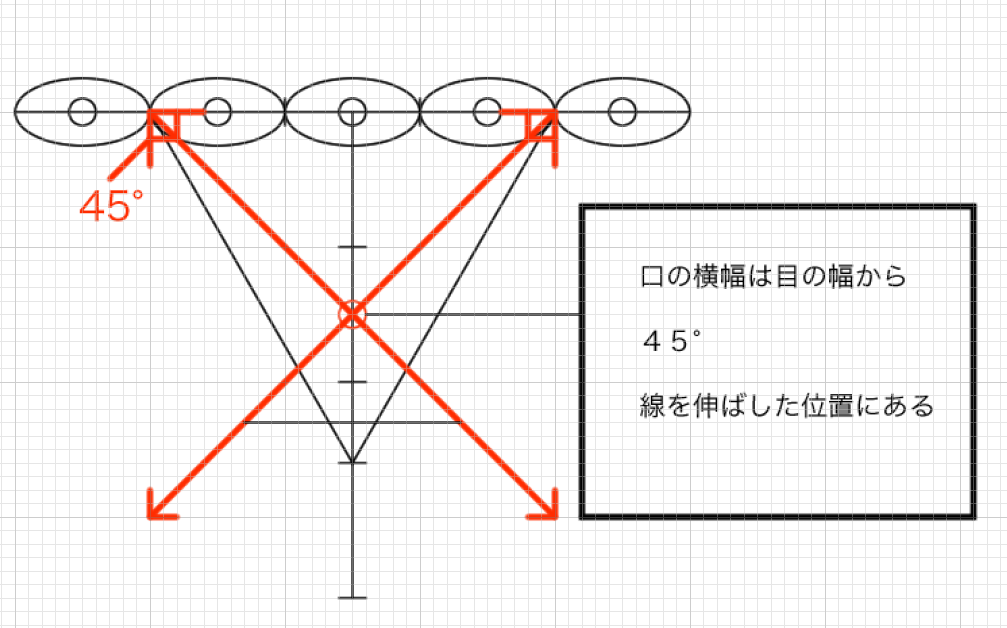
「鼻の高さ」は「顔の中央から目の端にかけての長さ」と等しい
(鼻の高さと目の幅の関係2)鼻の高さは顔の中央から目の端にかけての長さと等しい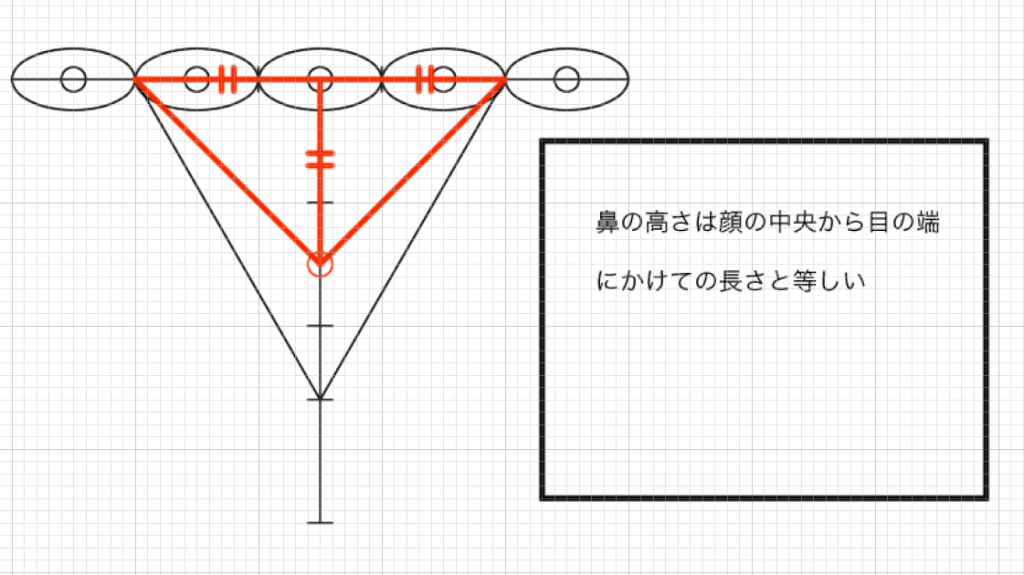
これは直角二等辺三角形であることがわかります。直角二等辺三角形の場合は「等しい長さの二辺」が生じます。「目と目の間の中心位置から目の端にかけての横幅」と「目と目の間の中心位置から鼻にかけての縦幅」の二辺は等しい長さであるということです。
「眉の高さ」は「鼻から顎にかけての高さ」の2つ分の位置にある
鼻から顎にかけての高さはすでに分かっています。目の幅から45°、もしくは顔の中央から目の端までの長さを使って出た鼻の位置から顎の高さを二倍した位置に眉があります。
(眉の高さと鼻の高さの関係)眉の高さは鼻から顎にかけての高さを2倍した高さ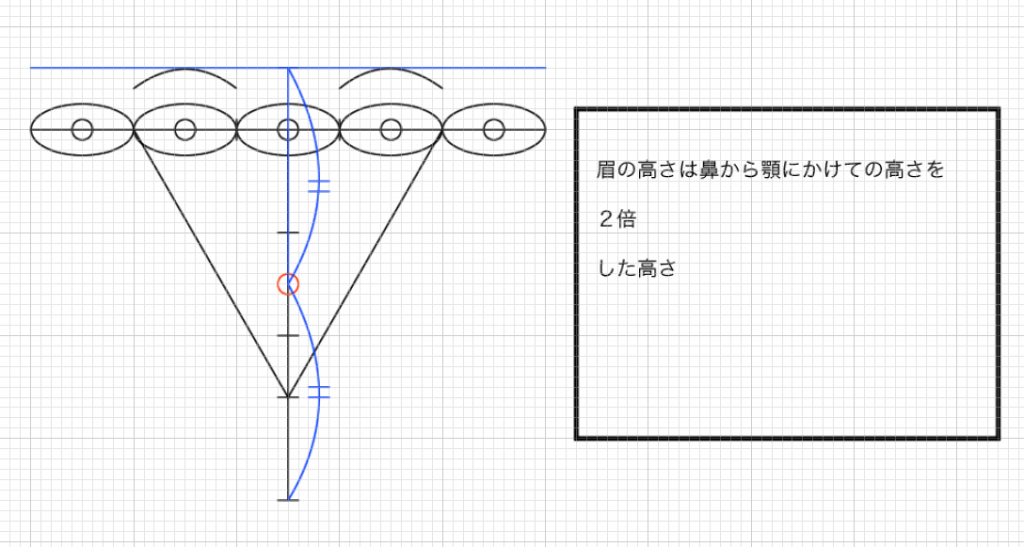
「生え際の位置」は「鼻から顎にかけての高さ」の3つ分の位置にある
これは言い方次第のところがあります。要するに「生え際から眉の高さ」=「眉から鼻の高さ」=「鼻から顎の高さ」ということです。
(生え際の位置)生え際から眉の高さ、眉から鼻の高さ、鼻から顎の高さ、この3つの高さは等しい

「生え際から頭頂までの高さ」は眉から鼻にかけての高さの1/2
(頭頂の位置)生え際から老鳥までの高さは眉から生え際までの高さの1/2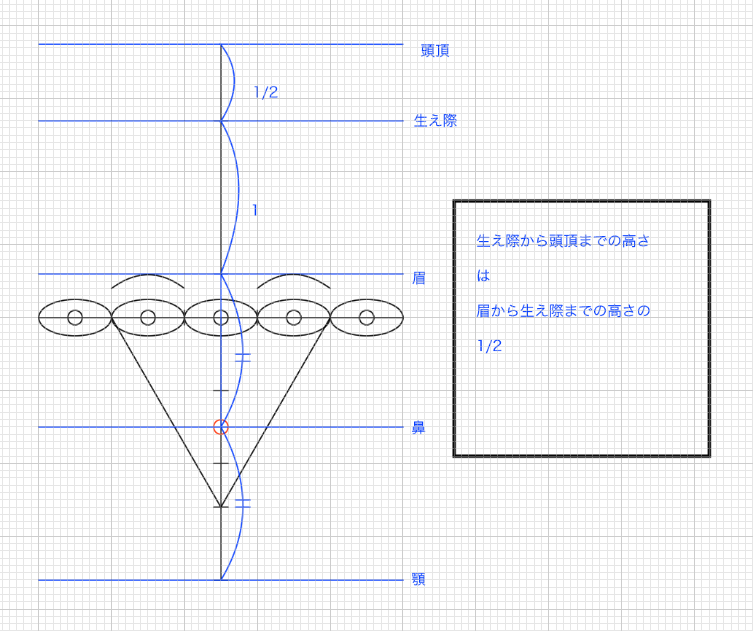
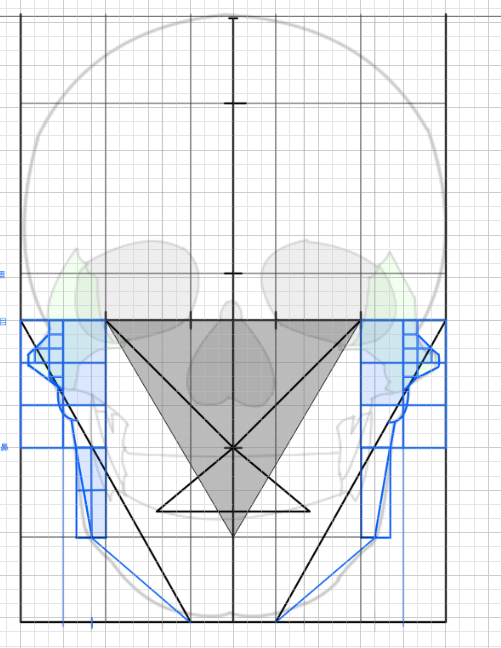
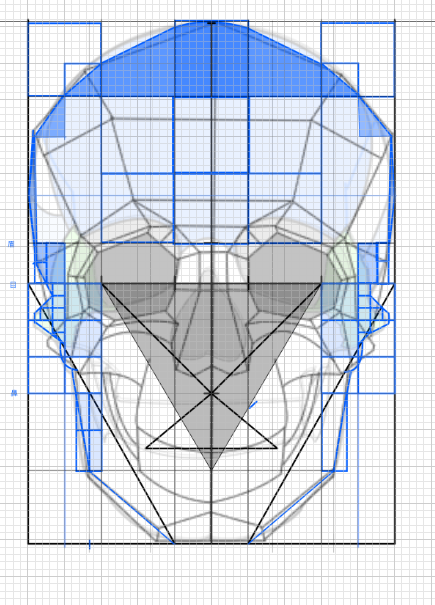
これで顔全体のだいたいの高さと幅がわかりました。
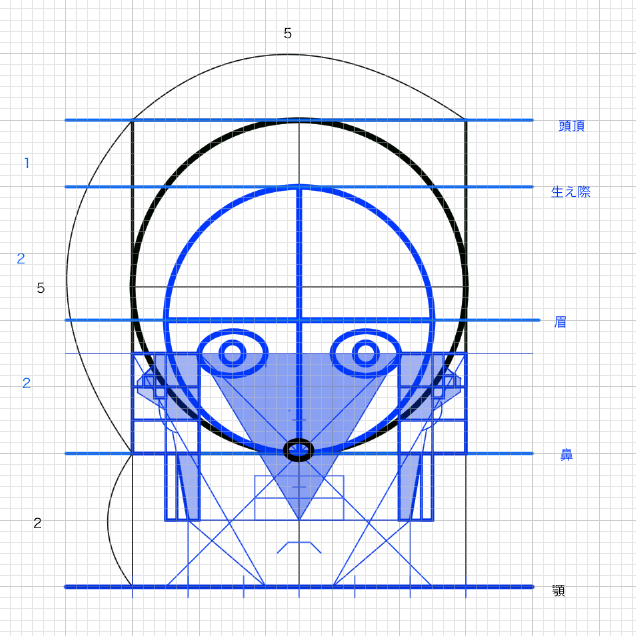
イメージの顔です。若干ずれてるのは参考にした顔の比率が少しずれてるからです(測りました)。これでイメージができると思います。
【顔の輪郭】あごについて
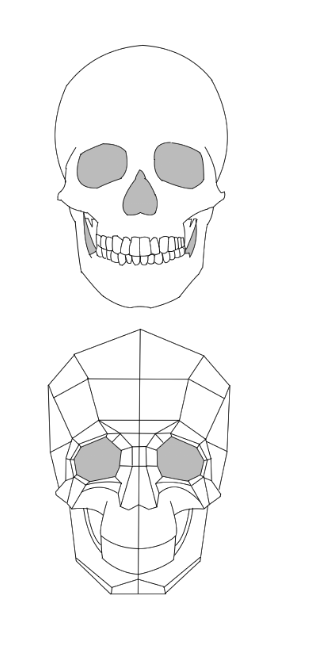
顔で厄介なのは輪郭です。目、鼻、口は配置的でも輪郭が上手く描けないことがあると思います。骨格や筋肉の理解は助けになるのでしょうか。考察してみます。
これは骨格のイメージです。骨格の輪郭と顔の輪郭はぴったり合うわけじゃありませんが、おおよその目安となります。

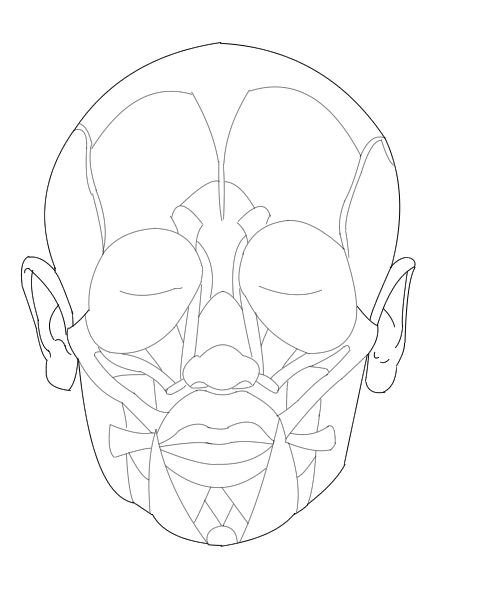
イメージばかりで申し訳ありません。イメージとしては骨格の上に筋肉が重なり、皮膚が重なる感じですね。
下顎(かがく)とはなにか
(下顎とは)下顎骨は下顎を形成する骨である。 ヒトの下顎骨は、上顎骨と対になっている骨であり、頭蓋の顔面骨の中で一番大きく、強い骨である。下顎の歯を釘植する。水平のU字状上に曲がっている下顎体と、その両端に垂直につく二つの下顎枝からなる。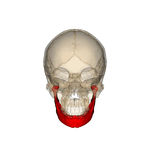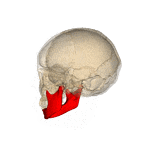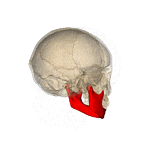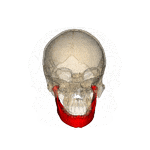 (ウィキペディア)
(ウィキペディア)
顔の輪郭を描くためには下顎を理解が必要です。下顎には下顎角というものがあります。この下顎角の位置によって輪郭は大きく変わります。
(下顎角とは)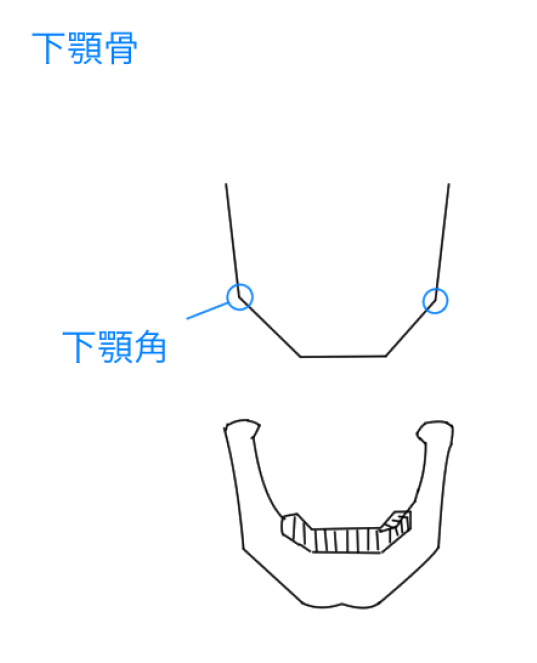 正面から見ると下顎は左右同じような長さで、あごに当たる部分は平らです。観察してみると左右の長さが対象になっているようにも思えます。もちろん正面・横向き・横顔で下顎角の見え方は異なります。正面だと左右は同じような長さでしたが、横向きになると片方が「短縮」されたように見えます。実際には骨の上に筋肉やら皮膚やらがあります。
正面から見ると下顎は左右同じような長さで、あごに当たる部分は平らです。観察してみると左右の長さが対象になっているようにも思えます。もちろん正面・横向き・横顔で下顎角の見え方は異なります。正面だと左右は同じような長さでしたが、横向きになると片方が「短縮」されたように見えます。実際には骨の上に筋肉やら皮膚やらがあります。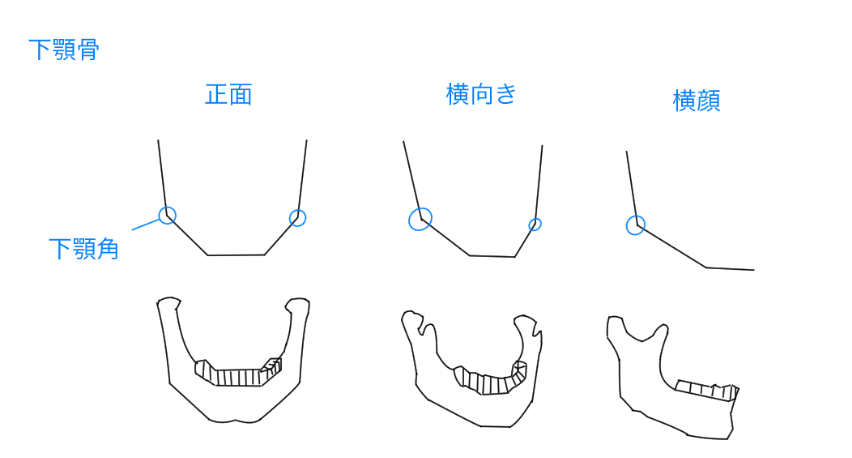
下顎の幅や高さについて
正面の場合顎の中心部分は平らになります。幅はおよそ目の幅と等しくなります。これはあくまでも目安です。男性と女性でも差異が出ます。
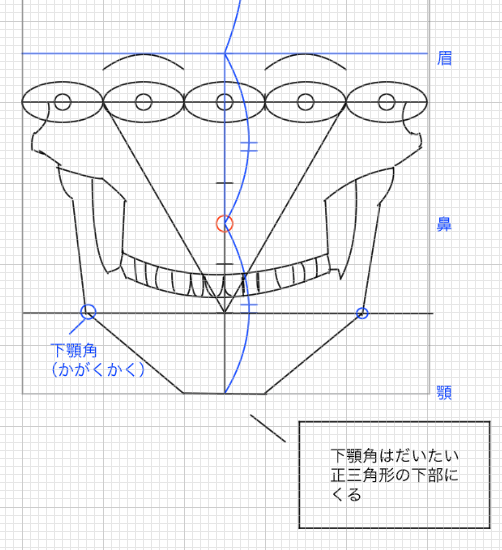
どらくらいの高さに下顎角があればいいのでしょうか。個人差はもちろんありますが、基本の下顎角位置というものがあるはずです。ここでいう下顎角位置は実際の下顎骨の位置とは異なります。肉や皮も含めた位置です。
正三角形のちょうど一番下にある高さなんてどうでしょうか。
皮膚や肉をつけるとこんなイメージになります。
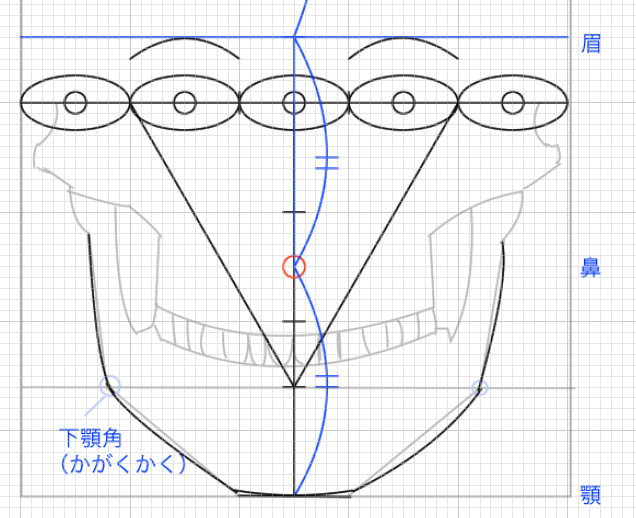
真正面から見ると下顎骨は左右対称で同じ長さ、同じ角度です。とりあえず首の位置くらいに下顎角をおいてみます。首はだいたい顔全体の横幅を1とした場合、2/3くらいの長さになります。顔の横幅全体を6分割した場合の、4/6(2/3)ほどです。顔半分の端1/3くらいを目安にしてもいいかもしれません。
顔の横幅全体は目の5つ分です。それを半分にすると左右に2.5となります。2.5/3でおよそ0.8です。つまり左右の目を左から右に0.8ほどの位置に首や下顎角があるということです。
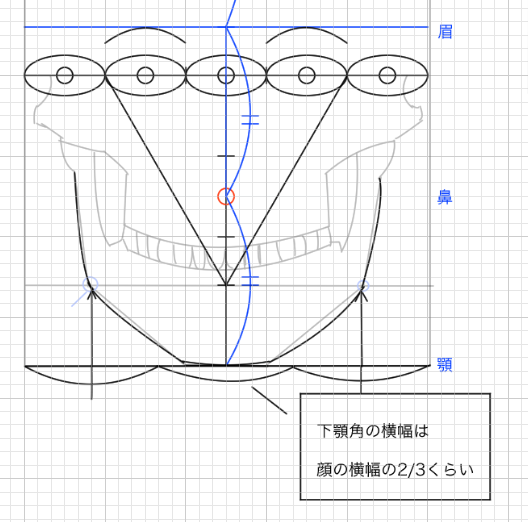
これも目安ですけど下顎骨はあごから顔の端に線を伸ばした位置の近くにあります。
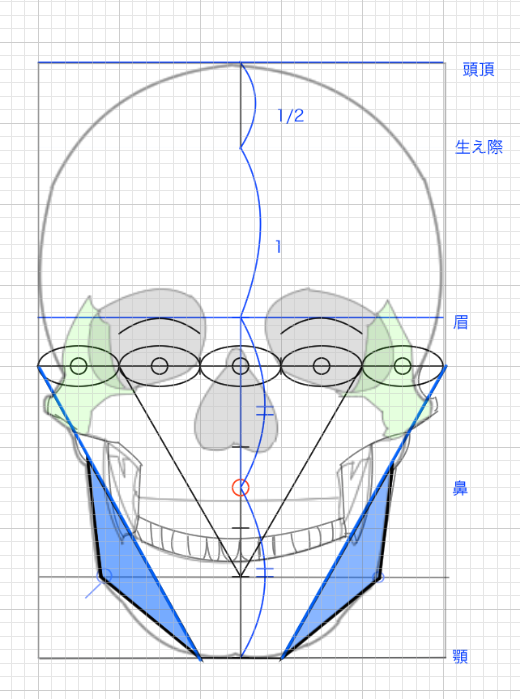
下顎骨の丸い部分はちょうど顔の端の目の中心に来るような来ないようなという感じですね。
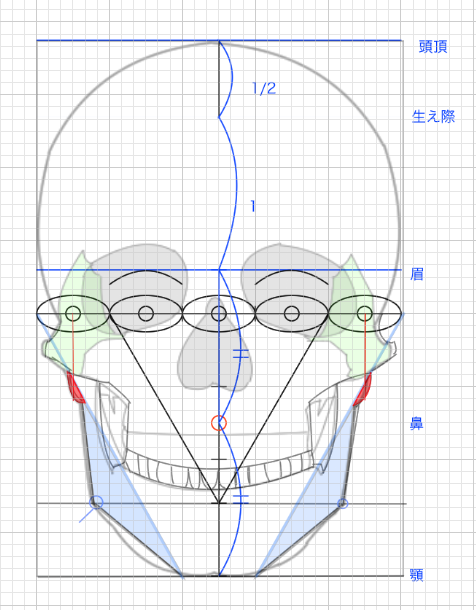
【顔の輪郭】頬骨について
顔の輪郭形成に解剖学的理解は有用だと思います。頬骨がどの部位か抑えましょう。
(頬骨の位置)
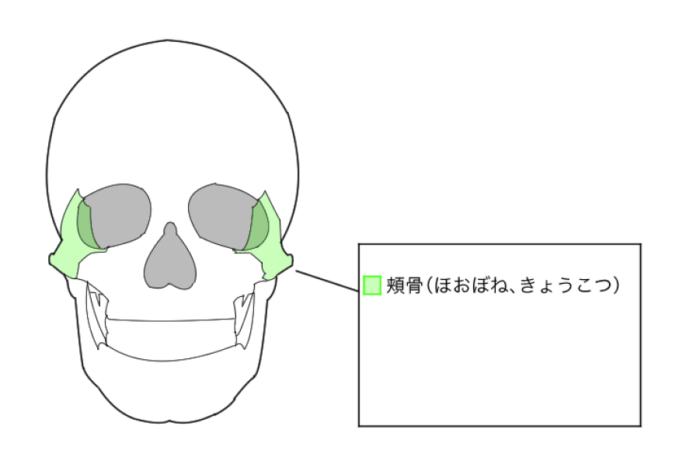
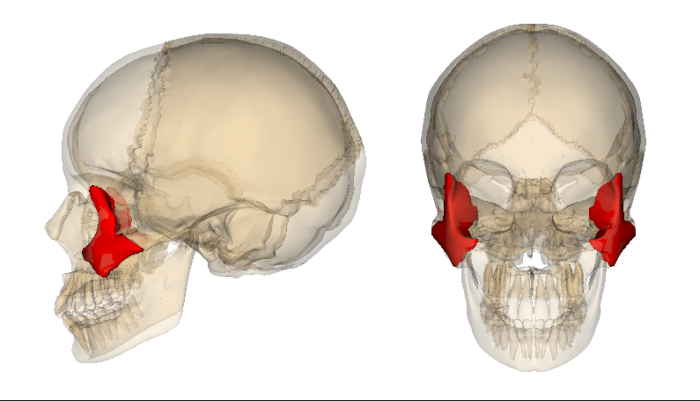
(wiki)
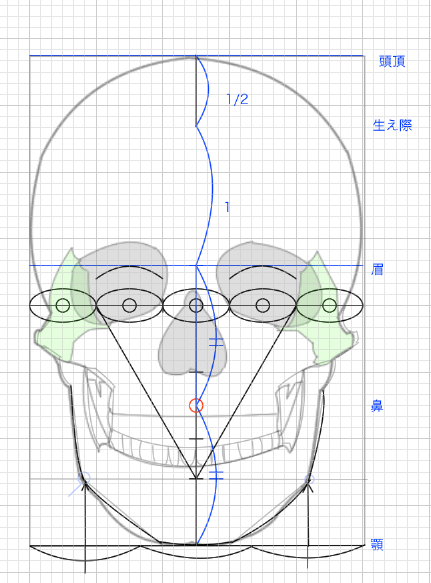
比率の把握には観察と分析が必要になります。自分でわかりやすい目安を見つけていきましょう。
【顔の輪郭】頭蓋について
頭蓋は個人的に一番難しい部位だと思います。
まずは基本的な頭蓋骨の名前を把握します。とりあえず正面だけ扱います。

そんなに曲線に拘る必要もないと思いますね。どうせ髪とか生やしてしまいますし。いわゆる単純化ですね。
球体と正三角形に関する考察
球体-いわゆるマルバツについて-
いままで正三角形を元に考察してきました。いわゆるルーミスなどは最初に球(あるいは円)を描いてそこから鼻や目を書き足すという手法です。
この球手法は正三角形と組み合わせて使うことが可能かどうか考察したいと思います。
球体手法においては鼻の部分に球体の下部がきます。ということは正三角形手法に当てはめるとおおよそこういうことになります。
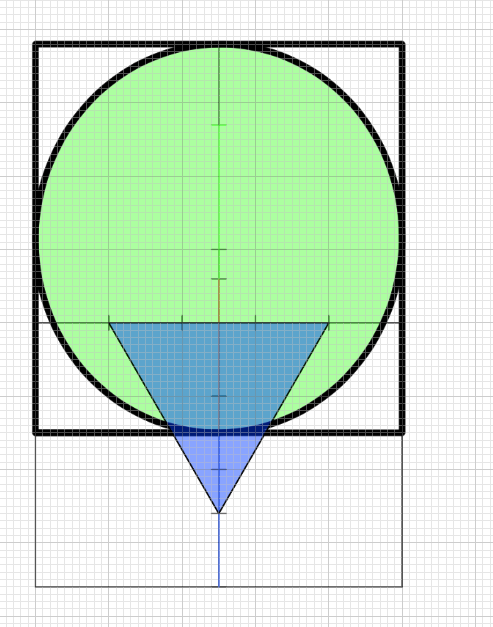
正三角形の一つの辺を1とした場合、眉から鼻にかけての長さは約2.1となります。そして眉から生え際にかけての長さも同じく2,1、生え際から頭頂にかけての長さは1.05となります。鼻から頭頂にかけての長さは眉から鼻にかけての長さ+眉から生え際にかけての長さ+生え際から頭頂にかけての長さとなり、5,25となります。そして横幅は5です。仮にこれを簡略化すると、2+2+1となり5になります。つまり5*5の正四角形、及び正円が作られます。

鼻から頭頂にかけては5(2,2,1)となります。
残念なことに正円の中心の線は眉の位置に当たりません。すこし下にずれます。眉の位置に球体の中央が来るにはどうすればいいか?という問題になります。
おそらくそれは簡単で、1:2:2なので。2:2の部分を使い4*4の円を作るという手法が考えられます。ただし横幅は5なので4は困ります。
鼻からあごにかけての長さは2です。

正三角形を入れてみます。以前は正三角形の1辺に対して高さを2.6でとっていましたが、簡略化のために2.5とします。
目というものは顔の高さの半分の位置にあるとよく教わる。そして原則的に高さの割合は1:2:2:2となる。つまり目の位置は3.5の位置にあるということだ。私の作ったモデルも2+1.5の位置(2は顎から鼻にかけて、1.5は鼻から目にかけての長さ)にあるのでちょうど半分の位置にあるので正しいといえる。
ルーミスのような○を書いて十字という方法を使うと、十字の位置に眉が来るらしい。しかし実際に丸で描いてみようとすると十字の位置に眉は来ない。実際にはすこし下にあるということだ。
実際に正円から顔を構成する方法を考察してみたい。この手法はデジタルというよりもアナログでいかに綺麗な顔を構成できるかということかもしれない。デジタルなら3Dツールを使ったほうが早いだろう。
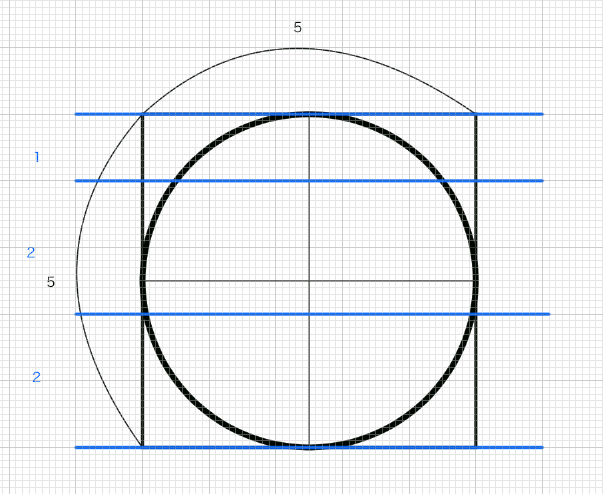
まずは正円を描く。

十字を描く
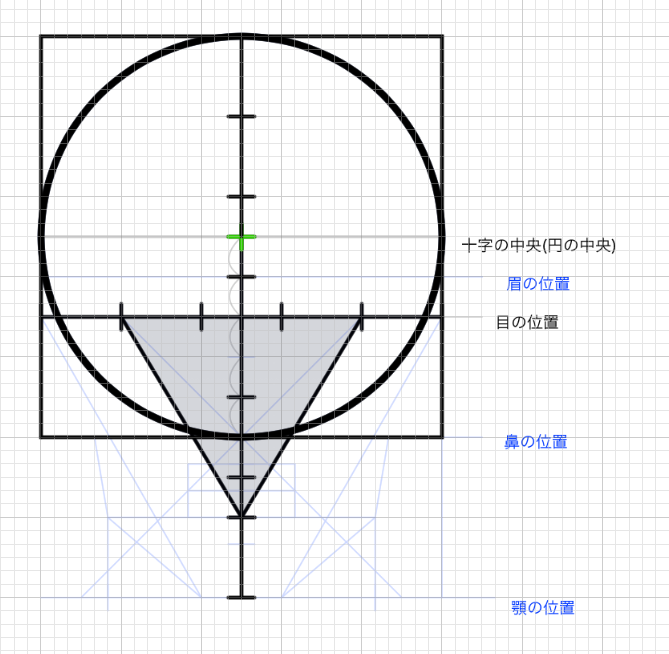
顔の全体の割合は1:2:2:2なので、幅は7ということになる。そして正円は1:2:2の部分つまり5にあたる。5の中央値は2.5なので、十字は2.5の位置に来る。
ということは、0.5単位で考えなければならない。正円の下部は2.5なので、5分割できる。眉の位置は5分割したうちの1分割の位置にある。
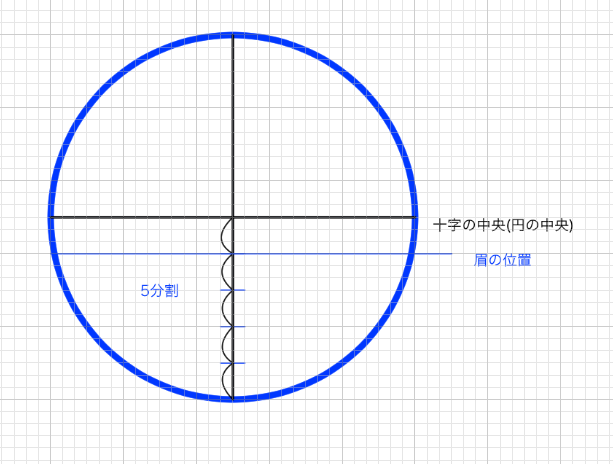
横幅も5分割を行い、正三角形を位置づける。そのためには目の位置を知らなければならない。目の位置は十字の中央から眉の位置にかけての長さを、眉の位置から目の位置にかけての長さにも伸ばしてあげれば分かる。
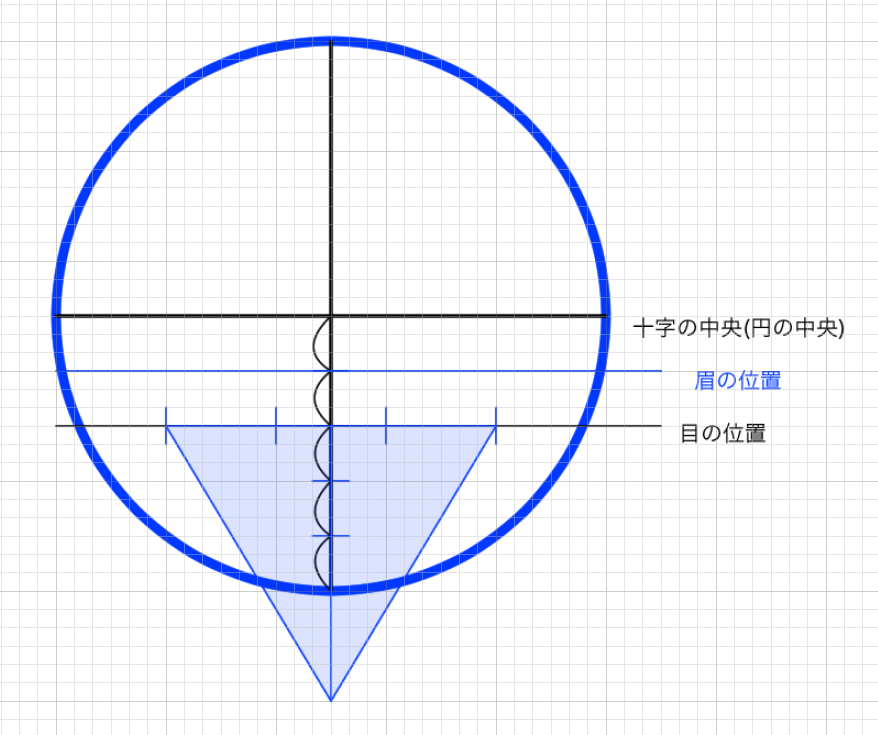
あとは眉の位置から鼻の位置(円の最下部)の位置を、あごにかけて伸ばしてあげれば全体の高さが決まる。単純に正三角形の下部を利用して、円の最下部から正三角形の最下部にかけての長さと等しい長さを伸ばしてあげてもいい。
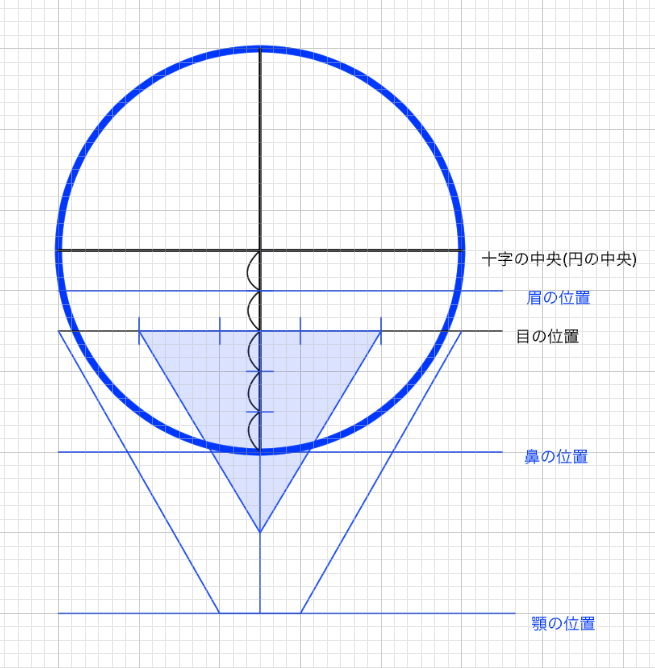
残りはまだ研究途中のところがあります。口については鼻から顎にかけての長さを3分割するとだいたいの位置がわかります。実際には肉や皮、耳がつきます。
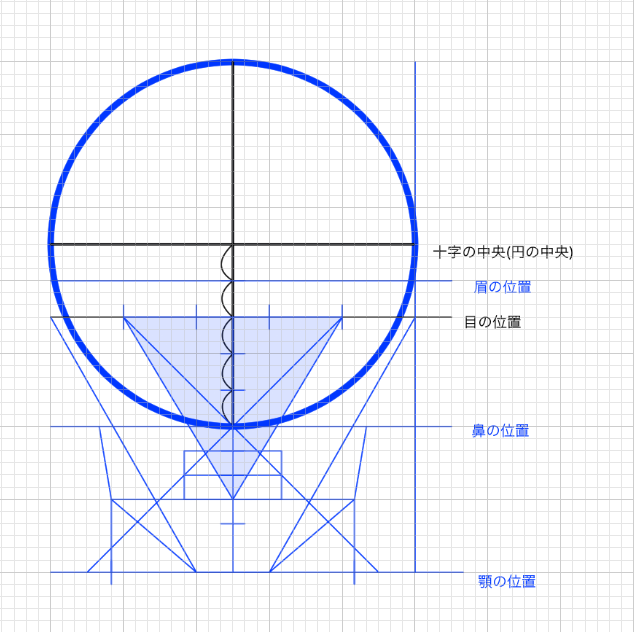
アナログではこの手法はかなりのバランス感覚が求められてしまう。つまり正確な円を描き、正確に5分割できなければいけない。これがなかなか難しい。
やはり最初は正三角形から作成し、それに円を描くという手法のほうがより正確に描ける気がする。
まずは辺が等しい3つを並べる。
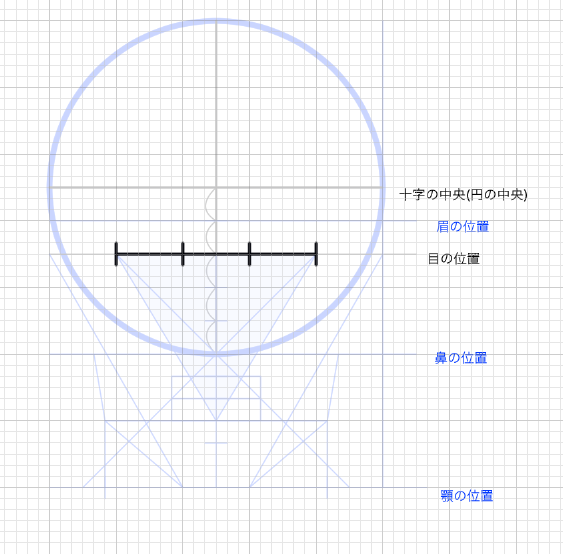
次に2.5の線を縦に伸ばして正三角形を作る。
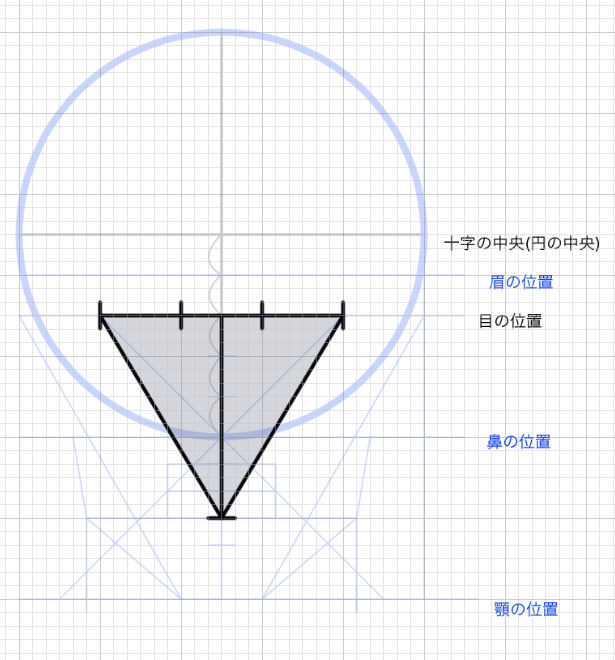
横幅にも等しい幅を加える
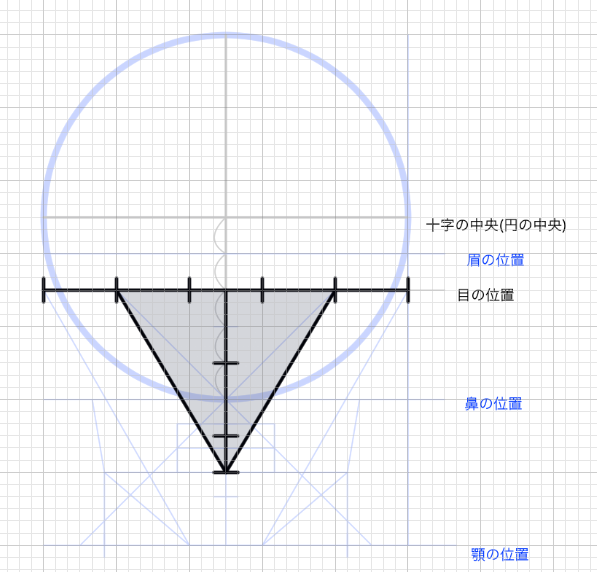
次に、縦に正三角形の1辺分の高さを加える。重要なのはこの位置が円の十字の中央に当たるということだ。同じ高さを下にも加える。
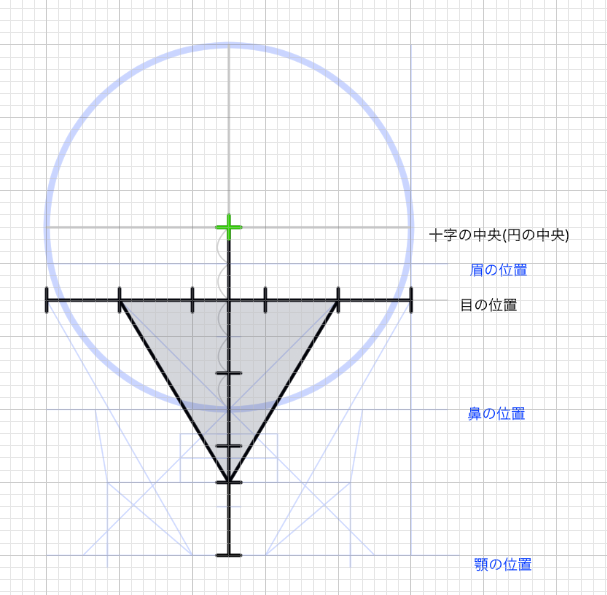
鼻は最初につくった2.5のうちの1.5の位置にある。重要なのはこの位置が円の最下部にあたるということだ。目の位置から顎の位置にかけての長さを、目の上にも加える。数値で言うと3.5を加える。十字から目の位置の中央に来るのは眉の位置である。
鼻の位置から頭頂にかけて、円を構成することができる。
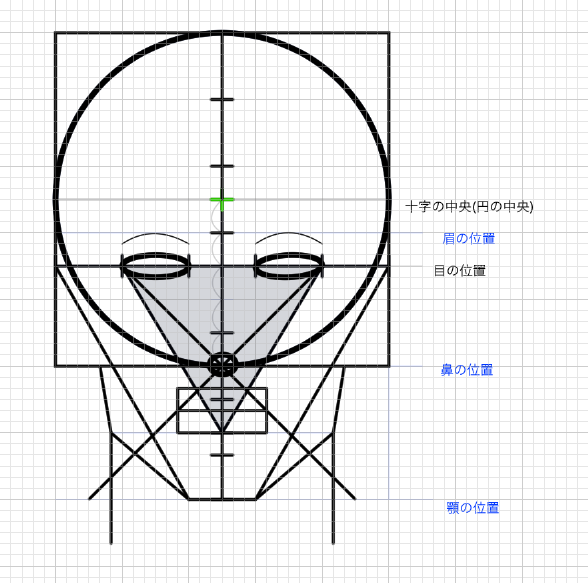
この手法のポイントは、最初の正三角形の3辺さえ描ければいいということだ。球から描くとバランス感覚が難しい。
正三角形とパースに関する考察
パースは意外と難しい。問題は正面から見ればきれいな正三角形を描くのは容易いが、斜めや横から見ると正三角形はどう描けばいいかということだ。
パースは奥に行けば行くほど小さく、短く見える。

これは実際には同じ長さの線であるにも関わらず、パースによって遠くのものは短く、近くのものは長く見えるということである。太陽は鉛筆より大きいはずなのに、目の前の鉛筆よりも太陽が小さく見えるのと同じだ。
3*3の正方形を二点透視図法で描いてみるとこうなる。
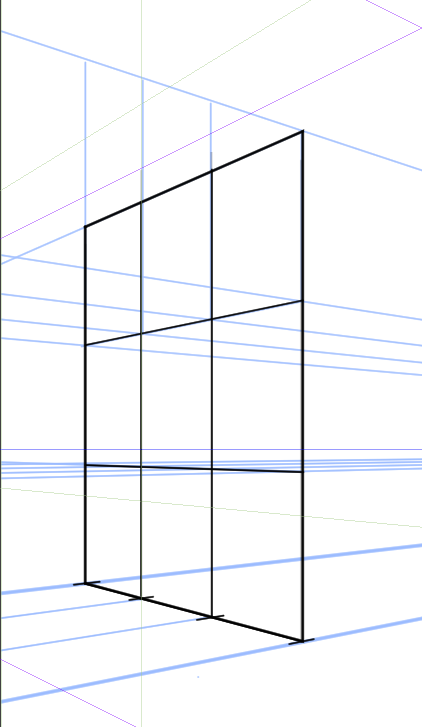
ここで正三角形をつくってみる。
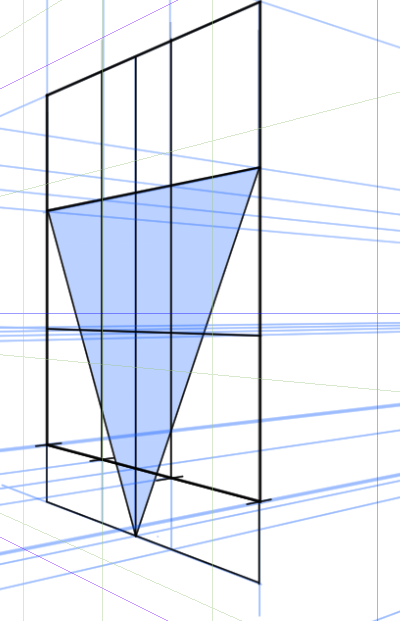
あとは正面と同じ手順でやってみる。これは慣れると簡單かもしれないがメンドクサイ。正面を自由変形したほうが早いかもしれない。もう少し研究する必要がある。
コメント
この記事へのトラックバックはありません。












この記事へのコメントはありません。